Revision NotesFlashcardsPast Papers
IGCSEMathsEdexcelMaths A (Modular)Higher Unit 1Revision NotesStatistics & ProbabilityProbability Diagrams: Venn & Tree DiagramsProbability Tree Diagrams

Probability Tree Diagrams (Edexcel IGCSE Maths A (Modular))

Revision Note

Mark Curtis

Written by: Mark Curtis

Reviewed by: Dan Finlay

Edexcel Maths A (Modular): Higher Unit 1Cambridge (CIE) International Maths: ExtendedCambridge (CIE) Maths: ExtendedEdexcel Maths A: HigherCambridge (CIE) International Maths: CoreCambridge (CIE) Maths: Core

Did this video help you?

Tree Diagrams

How do I draw a tree diagram?

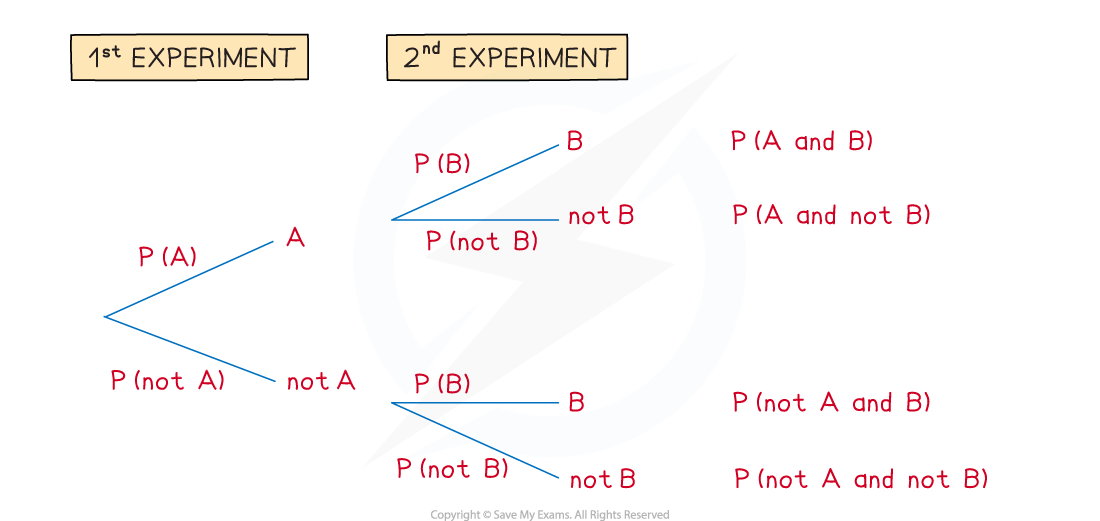
  • Tree diagrams can be used for repeated experiments with two outcomes

    • The 1st experiment has outcome A or not A

    • The 2nd experiment has outcome B or not B

  • Read the tree diagram from left to right along its branches 

    • For example, the top branches give A followed by B

      • This is called A and B

How to set up a tree diagram for two experiments each with two possible outcomes

How do I find probabilities from tree diagrams?

  • Write the probabilities on each branch

    • Remember that P(not A) = 1 - P(A)

      • Probabilities on each pair of branches add to 1

  • Multiply along the branches from left to right

    • This gives P(1st outcome and 2nd outcome)

  • Add between the separate cases

    • For example

      • P(AA or BB) = P(AA) + P(BB)

  • The probabilities of all possible cases add to 1

  • If asked to find the probability of at least one outcome, it is quicker to do 1 - P(none)

How do I use tree diagrams with conditional probability?

  • Probabilities that depend on a particular thing having happened first in a tree diagram are called conditional probabilities

  • For example, the probability that a team wins a game may depend on whether they won or lost the previous game

    • The probabilities for 'win' on the first set of branches may be different to those for 'win' on the second set of branches

  • Another example of conditional probabilities is "without replacement" scenarios

    • e.g. two items are drawn from a bag of different coloured items without the first item drawn being replaced

    • The probabilities on the second set of branches will change depending on which branch has been followed on the first set of branches

      • The denominators in the probabilities for the second set of branches will be one less than those on the first set of branches

      • The numerators on the second set of branches will also change

  • Conditional probability questions are sometimes introduced by the expression 'given that...'

    • e.g. 'Find the probability that the team win their next game given that they lost their previous game'

  • The notation straight P open parentheses A vertical line B close parentheses is often used for conditional probabilities

    • That is read as 'the probability of A given B'

    • e.g. straight P open parentheses win vertical line lose close parentheses is the probability a team wins, given that they lost the previous game

Examiner Tips and Tricks

  • When multiplying along branches with fractions, don't cancel fractions in your working

    • Having the same denominator makes them easier to add together!

Worked Example

A worker drives through two sets of traffic lights on their way to work.
Each set of traffic lights has only two options: green or red.
The probability of the first set of traffic lights being on green is 5 over 7.
The probability of the second set of traffic lights being on green is 8 over 9.

(a) Draw and label a tree diagram. Show the probabilities of every possible outcome.

Work out the probabilities of each set of traffic lights being on red, R
Use P(red) = 1 - P(green)

straight P open parentheses 1 to the power of st space straight R close parentheses equals 1 minus straight P open parentheses 1 to the power of st space straight G close parentheses equals 1 minus 5 over 7 equals 2 over 7
straight P open parentheses 2 to the power of nd space straight R close parentheses equals 1 minus straight P open parentheses 2 to the power of nd space straight G close parentheses equals 1 minus 8 over 9 equals 1 over 9

Draw the branches (with a label of G or R on the ends)
Write the probabilities above each branch
Calculate probabilities of each outcome by multiplying along the branches from left to right

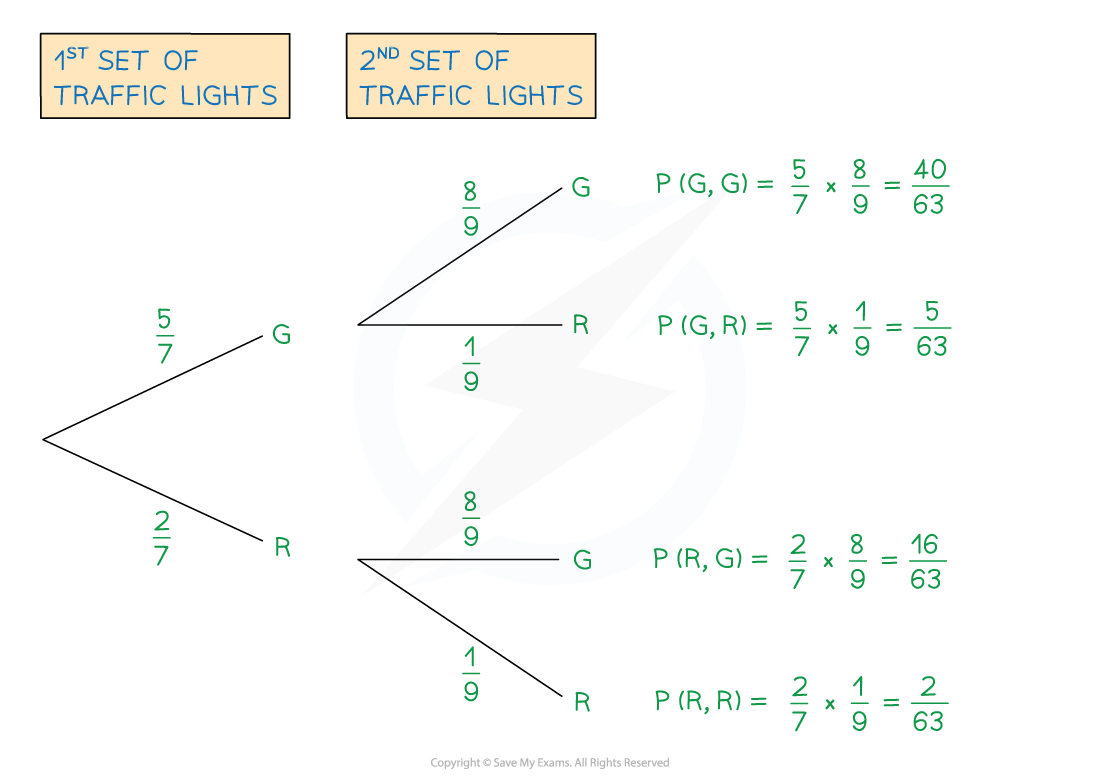
A tree diagram showing different outcomes at traffic lights

 (b) Find the probability that both sets of traffic lights are on red.

This is the answer for P(R, R) from the tree diagram

 bold 2 over bold 63

(c) Find the probability that at least one set of traffic lights are on red.

Method 1

This means the 1st is green and the 2nd is red
Or the 1st is red and the 2nd is green
Or the 1st is red and the 2nd is red ('at least one' could mean both)

Add between the separate cases

straight P open parentheses at space least space one space straight R close parentheses space equals space straight P open parentheses straight G comma space straight R close parentheses space plus space straight P open parentheses straight R comma space straight G close parentheses space plus space straight P open parentheses straight R comma space straight R close parentheses space equals space 5 over 63 space plus space 16 over 63 space plus space 2 over 63 space equals space 23 over 63

bold 23 over bold 63

Method 2

At least one red means all the possible cases shown except two greens

So P(at least 1 red) = 1 - P(two greens)

space 1 space minus space straight P open parentheses straight G comma space straight G close parentheses space equals space 1 space minus space 40 over 63 space equals space 23 over 63 

bold 23 over bold 63

Worked Example

Liana has 10 pets. She has 7 guinea pigs (G) and 3 rabbits (R).

Liana is choosing two pets to feature in her latest online video. 

First she is going to choose one of the pets at random.  Once she has carried that pet to her video studio she is going to go back and choose a second pet at random to also feature in the video.

(a) Draw and label a tree diagram including the probabilities of all possible outcomes.

For the 1st pet chosen, there will be a 7/10 probability of choosing a guinea pig, and a 3/10 probability of choosing a rabbit.

If the first pet is a guinea pig, there will only be 6 guinea pigs and 3 rabbits left (9 animals total)
So for the second pet the probability of choosing a guinea pig would be 6/9, and probability of choosing a rabbit would be 3/9

If the first pet is a rabbit, there will only be 7 guinea pigs and 2 rabbits left (9 animals total)
So for the second pet the probability of choosing a guinea pig would be 7/9, and probability of choosing a rabbit would be 2/9

Put these probabilities into the correct places on the tree diagram, and then multiply along the branches to find the probabilities for each outcome

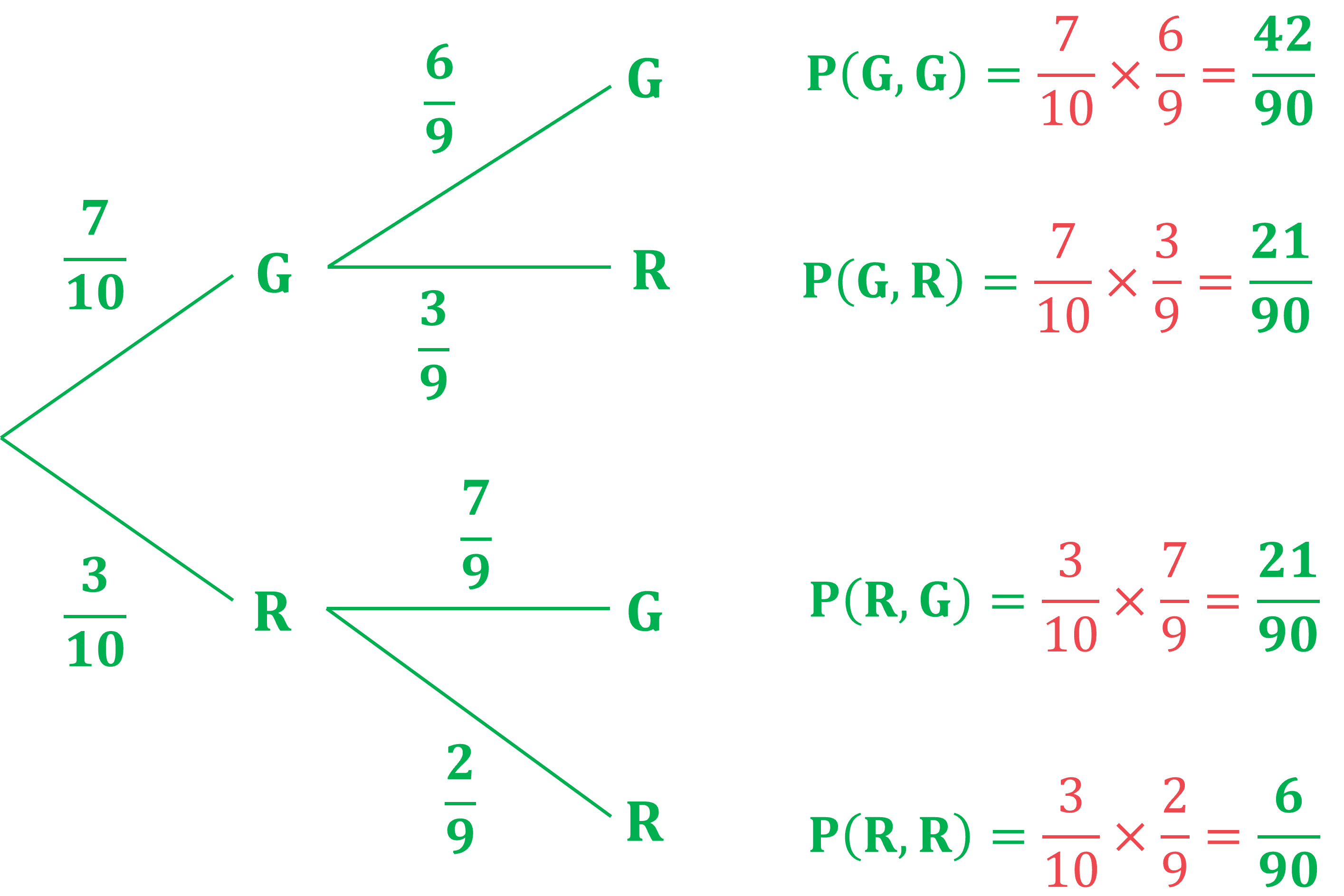
Tree diagram showing the information described in the question.

(b) Find the probability that Liana chooses two rabbits.

As we have already calculated this probability in the table, we can just write the answer down

Error converting from MathML to accessible text.

(c) Find the probability that Liana chooses two different kinds of animal.

This would be "G AND R" OR "R AND G" so we need to add two of the final probabilities

straight P open parentheses two space different space kinds close parentheses space equals space straight P open parentheses straight G comma space straight R close parentheses space plus space straight P open parentheses straight R comma space straight G close parentheses space equals space 21 over 90 plus 21 over 90 equals 42 over 90

Error converting from MathML to accessible text.

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Flashcards

    Did this page help you?

    Previous:Probabilities from Venn DiagramsNext:Combined Probability
    Author
    Reviewer
    Mark Curtis

    Author: Mark Curtis

    Expertise: Maths

    Mark graduated twice from the University of Oxford: once in 2009 with a First in Mathematics, then again in 2013 with a PhD (DPhil) in Mathematics. He has had nine successful years as a secondary school teacher, specialising in A-Level Further Maths and running extension classes for Oxbridge Maths applicants. Alongside his teaching, he has written five internal textbooks, introduced new spiralling school curriculums and trained other Maths teachers through outreach programmes.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.