Simplifying Surds (Edexcel IGCSE Maths A (Modular)): Revision Note

Surds & exact values

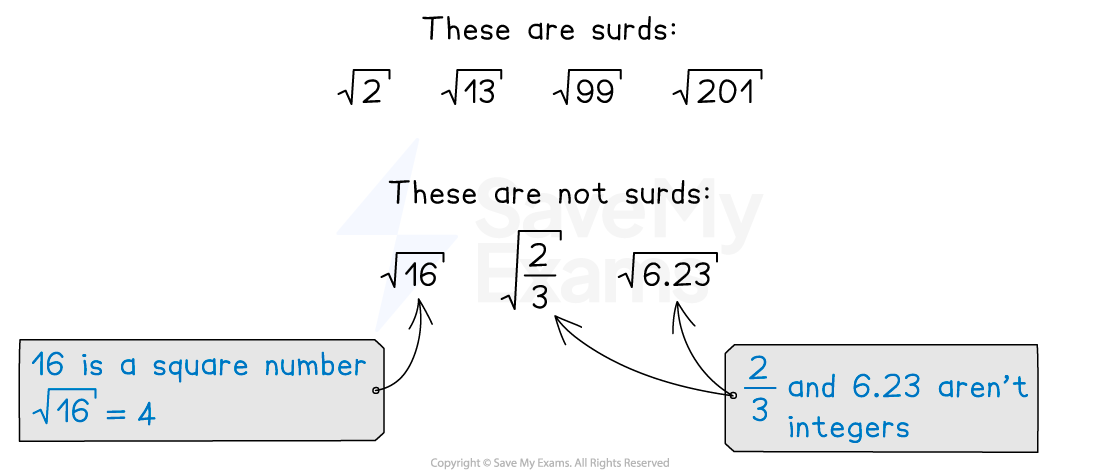
What is a surd?

• A surd is the square root of a non-square integer

• Using surds lets you leave answers in exact form

  • e.g.   rather than 

How do I do calculations with surds?

•  Multiplying surds

  • You can multiply numbers under square roots together

  • 

• Dividing surds

  • You can divide numbers under square roots

  • 

• Factorising surds

  • You can factorise numbers under square roots

  • 

• Adding or subtracting surds

  • You can only add or subtract multiples of “like” surds

    • This is similar to collecting like terms when simplifying algebra

  • 

  • 

    • However cannot be simplified

  • You cannot add or subtract numbers under square roots

  • Consider  

    • This is not equal to 

Simplifying surds

How do I simplify surds?

• To simplify a surd, factorise the number using a square number, if possible

  • If multiple square numbers are a factor, use the largest

• Use the fact that and then work out any square roots of square numbers

  • E.g.

• When simplifying multiple surds, simplify each separately

  • This may produce surds which can then be collected together

    • E.g. can be rewritten as

    • This simplifies to

    • These surds can then be collected together

    • 

• You may have to expand double brackets containing surds

  • This can be done in the same way as multiplying out double brackets algebraically, and then simplifying

  • The property  can be used to simplify the expression, once expanded

  • E.g. expands to

    • This simplifies to which gives