Equations of Straight Lines (y = mx + c) (Edexcel IGCSE Maths A (Modular)): Revision Note
Exam code: 4XMAF/4XMAH
Did this video help you?
Finding equations of straight lines
What is the equation of a straight line?
The general equation of a straight line is y = mx + c where
m is the gradient
c is the y-intercept
The value where it cuts the y-axis
y = 5x + 2 is a straight line with
gradient 5
y-intercept 2
y = 3 - 4x is a straight line with
gradient -4
y-intercept 3
How do I find the equation of a straight line from a graph?
Find the gradient by drawing a triangle and using
Positive for uphill lines, negative for downhill
Read off the y-intercept from the graph
Where it cuts the y-axis
Substitute these values into y = mx + c
What if no y-intercept is shown?
If you can't read off the y-intercept
find any point on the line
substitute it into the equation
solve to find c
For example, a line with gradient 6 passes through (2, 15)
The y-intercept is unknown
Write y = 6x + c
Substitute in x = 2 and y = 15
15 = 6 × 2 + c
15 = 12 + c
Solve for c
c = 3
The equation is y = 6x + 3
What are the equations of horizontal and vertical lines?
A horizontal line has the equation y = c
c is the y-intercept
A vertical line has the equation x = k
k is the x-intercept
For example
y = 4
x = -2
Worked Example
(a) Find the equation of the straight line shown in the diagram below.
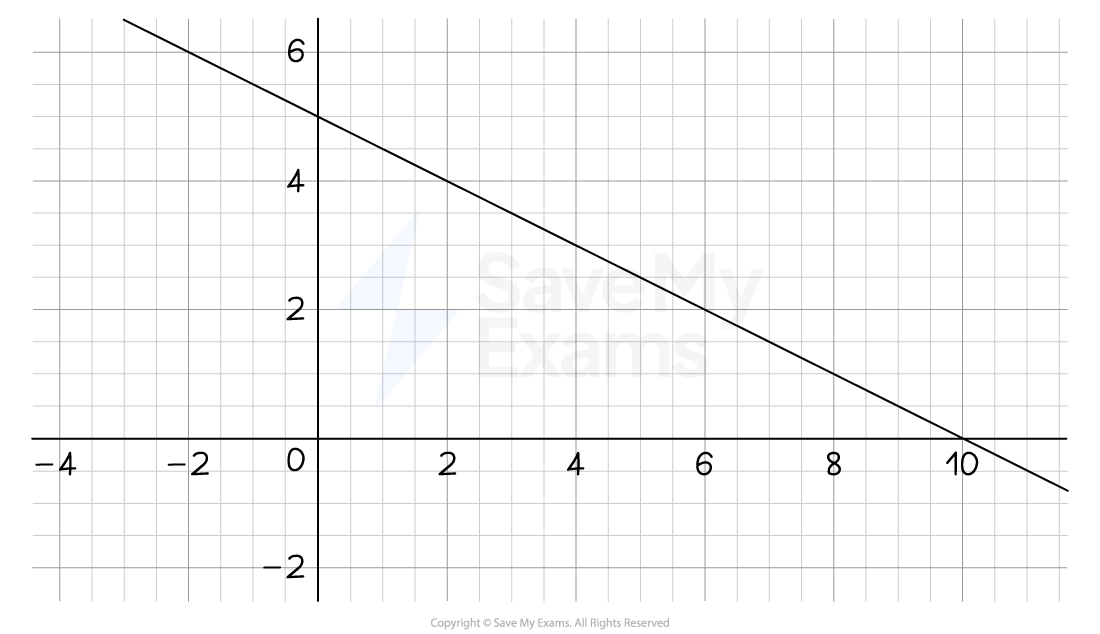
Answer:
Find m, the gradient
Identify any two points the line passes through and work out the rise and run
Line passes through (2, 4) and (10, 0)
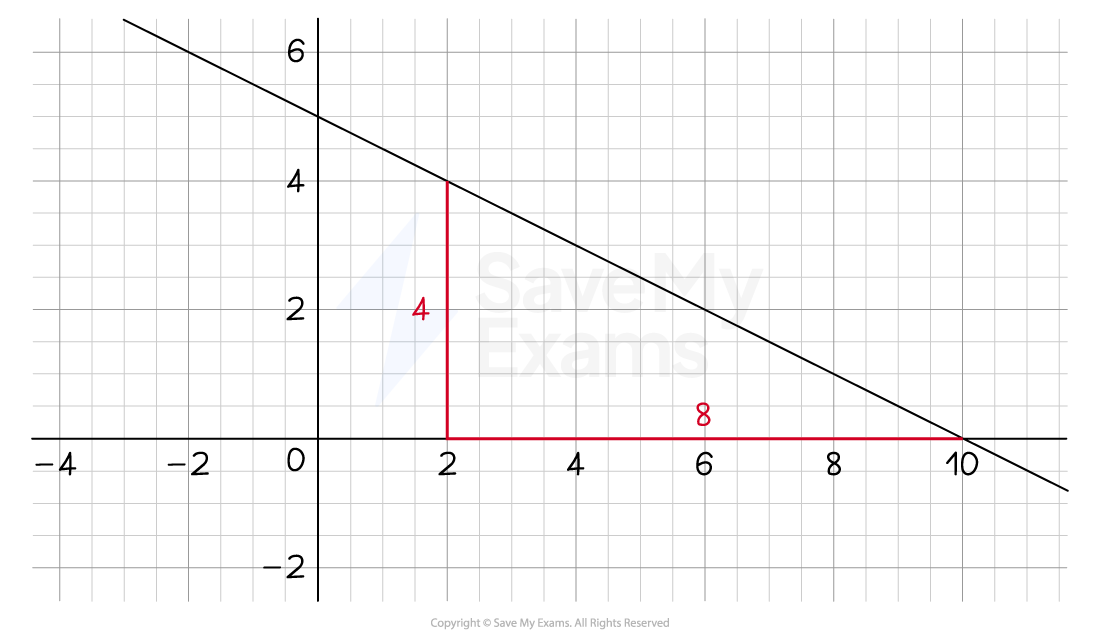
The rise is 4
The run is 8
Calculate the fraction
The slope is downward (downhill), so it is a negative gradient
gradient,
Now find the y-intercept
The line cuts the y-axis at 5
y-intercept,
Substitute the gradient, m, and the y-intercept, c, into y = mx + c
(b) Find the equation of the straight line with a gradient of 3 that passes through the point (5, 4).
Answer:
Substitute m = 3 into y = mx + c
Leave c as an unknown letter
Substitute x = 5 and y = 4 into the equation
Solve the equation to find c
You now know c
Replace c with −11 to complete the equation of the line

Unlock more, it's free!
Did this page help you?