This task looks at models for daily road traffic on a circular ring road around a city.
To help reduce the amount of traffic, the mayor of the city has implemented a new daily driving charge on the ring road, which will last for a year.
The scatter graph below shows the number of vehicles per day, , measured in tens of thousands, that use the ring road against the time,
, measured in months, from the date of the driving charge being introduced.
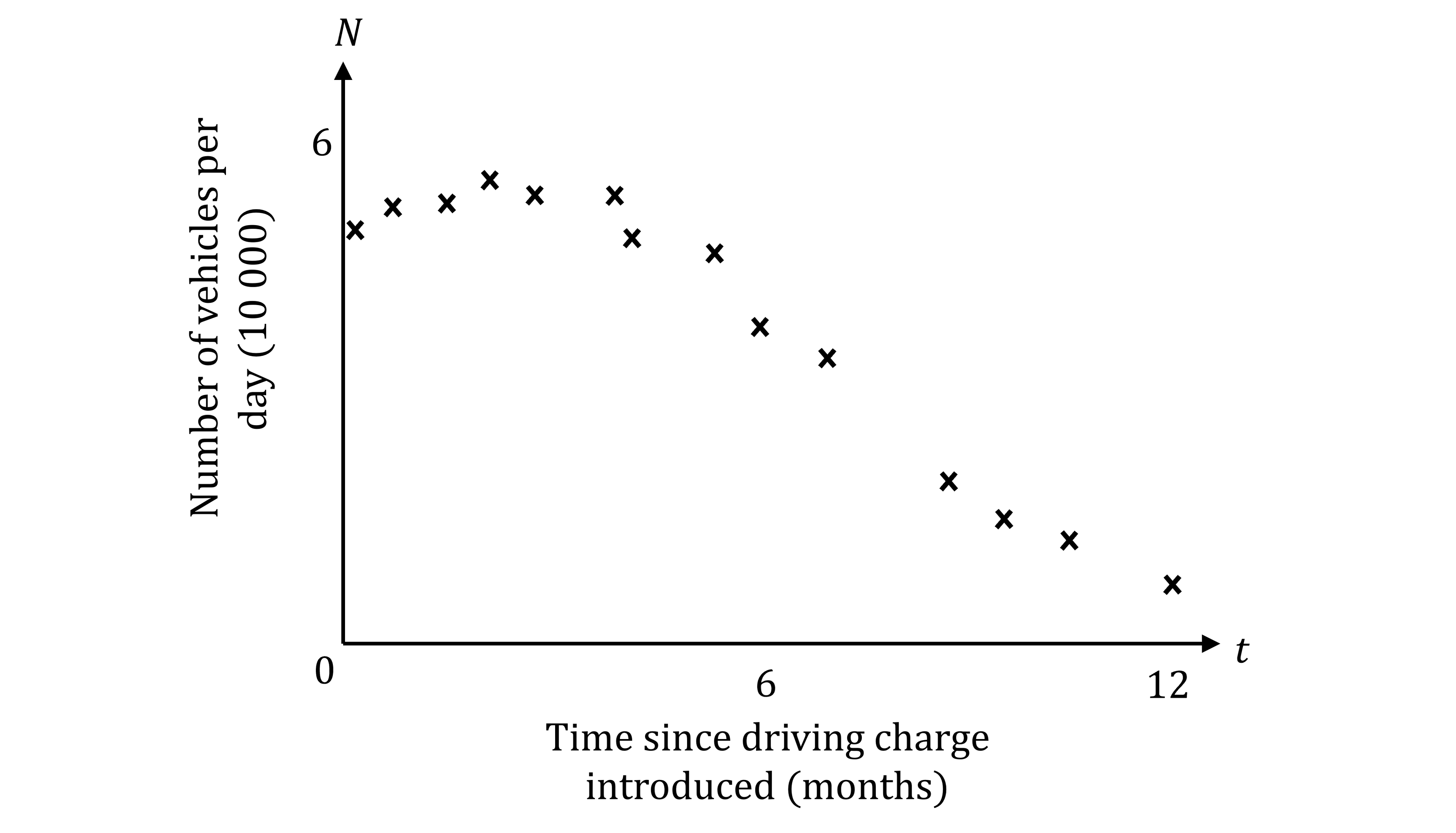
A simple model to relate and
is given by the line of best fit:
The line of best fit intersects the -axis at the point
and passes through the point
, as shown.
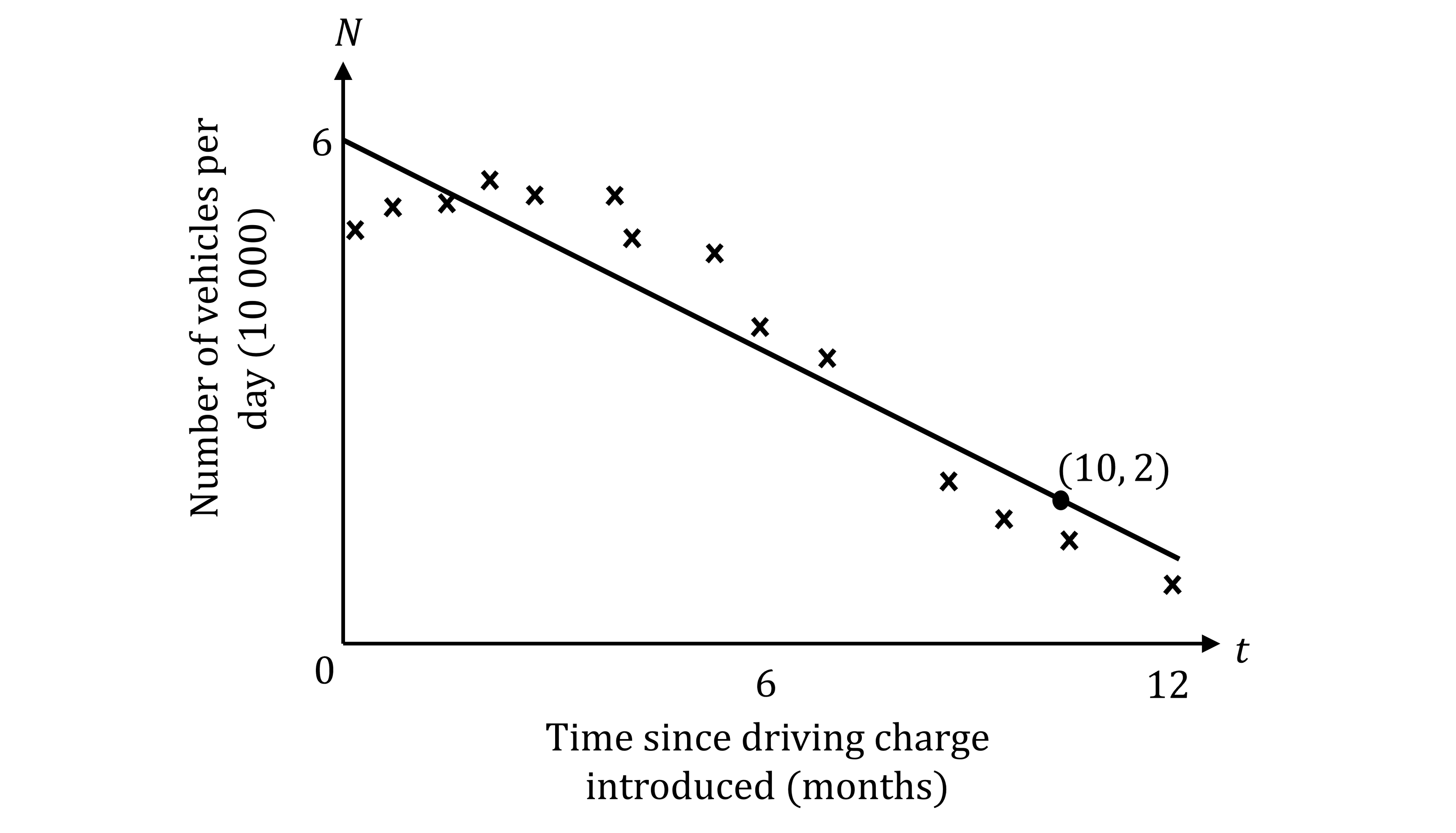
Use this information to find the values of and
.
Use the model in part (a) to predict the total number of vehicles per day on the ring road 7 months after the driving charge was introduced.
Explain, with reason, whether or not the line of best fit should be continued beyond 12 months.
Was this exam question helpful?

