This task looks at how to model the path of a bending river, using approximations to predict the speed of the river.
When viewed from above or drawn on a map, the path of a river is not a straight line but instead has many bends, especially as the river approaches the sea.
An S-bend is a bend in one direction followed immediately by a bend in the opposite direction. The map below shows a river path completing two identical S-bends before it reaches the sea (the water in the river flows from right to left).
The -axis is the centre line of the river path, about which the river bends, measured inland from the sea. The
-axis is perpendicular to the
-axis. The units on both axes are kilometres.
The flat land either side of the river path is called the flood plain. The lines and
indicate the boundaries of the flood plain.
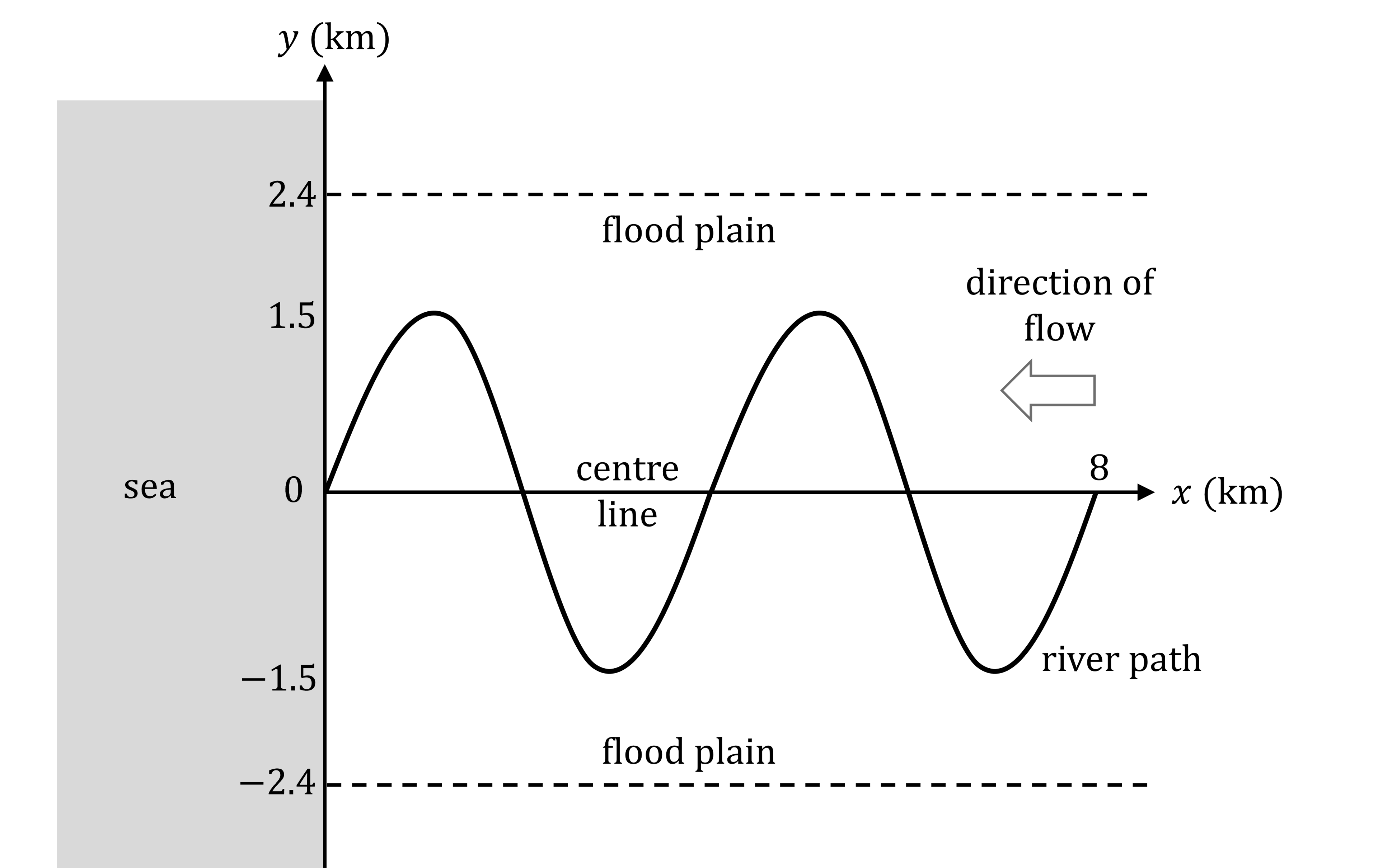
The amplitude, km, of an S-bend is the maximum distance (in the
-direction) from the centre line to the river path. From the diagram above:
The wavelength, km, of an S-bend is the distance along the
-axis that it takes to complete one S-bend.
Find the value of from the diagram.
A geographer wants to model the river path shown in part (a).
They suggest two possible models, where angles are measured in degrees:
Decide which of the models is not suitable for the river shown in the diagram.
Give a reason for your answer.
Substitute the values of and
into the correct model from part (b).
Simplify your answer.
Use the model in part (c) to find the perpendicular distance from the point on the centre line that is 500 metres inland from the sea, to the path of the river.
Give your answer correct to 3 significant figures.
Did this page help you?


