Investigations (Cambridge (CIE) IGCSE International Maths: Extended)

Exam Questions

1 hour18 questions

1 mark

This investigation introduces and explores the properties and patterns of the sequence of hexagonal numbers.

Hexagonal numbers are numbers formed by summing equally spaced dots around hexagons that sit inside of each other, as shown below.

If $n$ is the position of the term in the sequence then $H_{n}$ is the $n$ th hexagonal number.

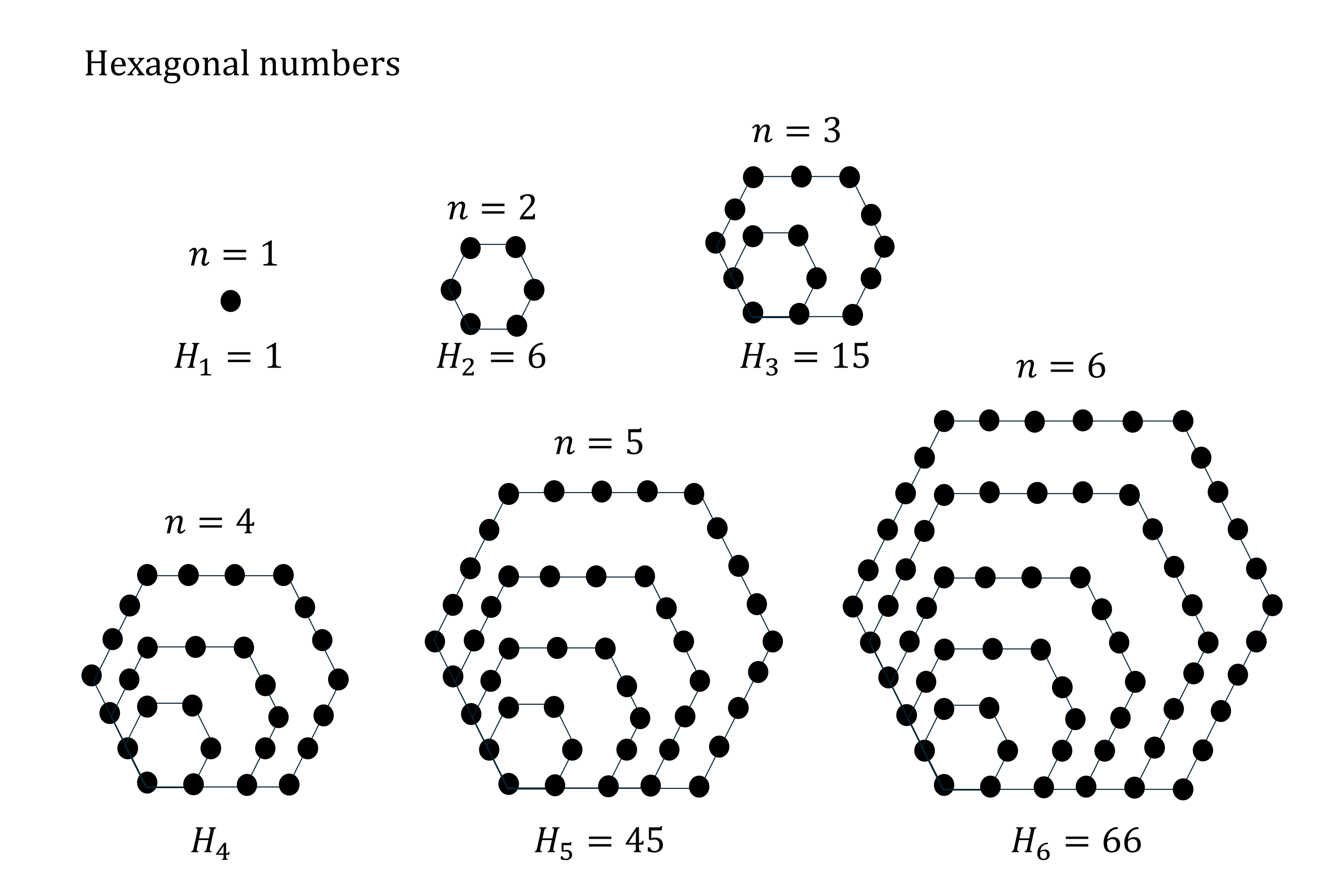
By counting the total number of dots in the diagram for $n = 4$ , work out the fourth hexagonal number, $H_{4}$ .

How did you do?

Did this page help you?

2 marks

The sequence of hexagonal numbers, $H_{n}$ , are shown below.

The missing value, $H_{4}$ , is your answer to question 1.

$n$	1	2	3	4	5	6
$H_{n}$	1	6	15		45	66

A new sequence, $K_{n}$ , is formed using the $n$ th term formula:

The first three terms, $K_{1}$ , $K_{2}$ and $K_{3}$ , are shown in the table below.

Find $K_{4}$ , $K_{5}$ and $K_{6}$ .

How did you do?

3 marks

A fraction is said to be a perfect square if it can be written in the form ${(\frac{a}{b})}^{2}$ where $a$ and $b$ are non-zero integers.

Terms in the sequence of $K_{n}$ can be made into fractions by dividing the previous term, $K_{n - 1}$ , by the current term:

$\frac{K_{n - 1}}{K_{n}} = \frac{previous term}{current term}$

Use the table below to show that fractions formed in this way are perfect squares.

The first example has been done for you, as follows:

$\frac{K_{1}}{K_{2}} = \frac{2}{8} = \frac{1}{4} = {(\frac{1}{2})}^{2}$

How did you do?

3 marks

By substituting the $n$ th term formula

$H_{n} = 2 n^{2} - n$

into the formula

$K_{n} = n + H_{n}$

and simplifying, use algebra to prove that

$\frac{K_{n - 1}}{K_{n}} = \frac{{(n - 1)}^{2}}{n^{2}}$

How did you do?

Did this page help you?