Investigations (Cambridge (CIE) IGCSE International Maths: Extended): Exam Questions

1 hour18 questions

2 marks

This investigation looks at the geometry and properties of an ellipse, including its area and its circumference.

An ellipse can be thought of as a squashed or stretched circle.

It can be described by a horizontal length, $a$ , and a vertical length, $b$ , measured from its centre, as shown below.

When $a = b$ , the ellipse is a circle with radius $a$ .

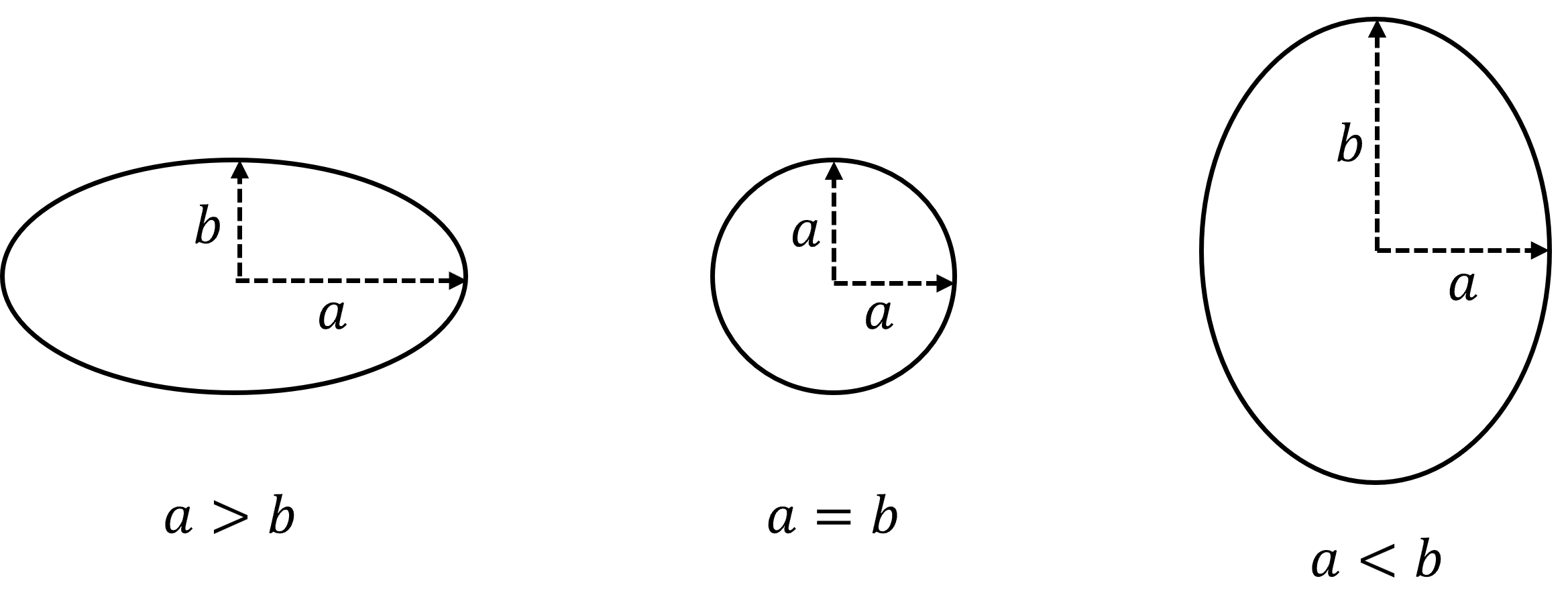
Three shapes: a horizontal ellipse with a greater width than height labelled 'a > b,' a circle labeled 'a = b,' and a vertical ellipse labelled 'a < b.'

This investigation will only consider ellipses in the form $a \geq b$ .

Sketch an ellipse with $a = 5$ and $b = 2$ .

Label the two lengths on your diagram.

How did you do?

1 mark

The formula for the area of an ellipse, $A$ , is given by

$A = π a b$

Complete the table below, leaving all answers in terms of $π$ .

The first example has been done for you:

$A = π \times 5 \times 2 = 10 π$

$a$	$b$	$A$
$5$	$2$	$10 π$
$8$	$3$
	$3$	$36 π$
$10$		$50 π$

How did you do?

Did this page help you?

3 marks

A minor circle refers to the biggest circle that fits inside an ellipse, with the same centre, as shown.

Diagram of an ellipse with a dashed inner circle, labelled "minor circle."

A major circle refers to smallest circle that fits outside an ellipse, with the same centre, as shown.

Diagram showing an ellipse inside a dashed major circle, labelled "major circle."

The following notation will be used for the different areas:

$A_{E}$ is the area of an ellipse
$A_{C}$ is the area of its minor circle
$A_{D}$ is the area of its major circle

Complete the table below, leaving answers fully simplified and in terms of $π$ (where necessary).

Parts of the table have been done for you.

$a$	$b$	$\frac{a}{b}$	$A_{E}$	$A_{C}$	$\frac{A_{E}}{A_{C}}$	$A_{D}$	$\frac{A_{E}}{A_{D}}$
$8$	$2$	$4$	$16 π$	$4 π$	$4$	$64 π$	$\frac{1}{4}$
$10$	$5$	$2$	$50 π$	$25 π$	$2$
$12$	$4$

How did you do?

Did this page help you?

2 marks

The area of a circle, radius $R$ , is equal to the area of an ellipse, $π a b$ .

A circle, radius R, with the same area as the ellipse. — **A circle, radius R, with the same area as the ellipse**

Use algebra to show that

$R = \sqrt{a b}$

How did you do?

2 marks

There is no algebraic formula for the circumference of an ellipse, $C$ .

However, there are many formulas that give approximations to the circumference of an ellipse in the form

$2 π r$

One approximate formula uses $r = \sqrt{a b}$ from part (a), giving:

$C_{1} = 2 π \sqrt{a b}$

A second approximate formula uses $r$ as the mean of $a$ and $b$ , giving:

$C_{2} = 2 π (\frac{a + b}{2})$

The table below compares the approximations $C_{1}$ and $C_{2}$ to the true circumferences, $C$ .

Complete the table, giving answers correct to 1 decimal place.

The first two rows have been done for you.

$a$	$b$	$C$	$C_{1}$	$C_{2}$
10	9	59.7	59.6	59.7
10	1	40.6	19.9	34.6
15	13	88.1
15	2	61.6

How did you do?

2 marks

Explain, with evidence from the table in part (b), which approximation out of $C_{1}$ and $C_{2}$ you would not recommend for ellipses that are very flat.

How did you do?

Did this page help you?

Investigations (Cambridge (CIE) IGCSE International Maths: Extended): Exam Questions

Investigations & Modelling

Investigations

Investigation: Hexagonal Numbers

Investigation: Ellipses

Investigation: Division by 11

Modelling

Modelling: Road Traffic

Modelling: App Downloads

Modelling: River Bends