Linear Regression Lines (Cambridge (CIE) IGCSE International Maths)

Revision Note

Written by: Naomi C

Reviewed by: Dan Finlay

Linear Regression Lines

What is a linear regression line?

Statistical software can calculate the equation for an 'ideal' line of best fit
- This 'ideal' line of best fit is known as a regression line
  - It is more accurate than a line of best fit drawn by eye
- You will be expected to use your graphic display calculator to generate the equation of linear regression
  - You do not need to calculate the equation by hand
An equation of a linear regression line is usually given in the form $y = m x + b$
- $b$ is the y-intercept of the regression line
- $m$ is the gradient of the regression line
- Both of those have the same meaning that they do for any line of best fit

How do I find the equation of a regression line using my graphic display calculator?

You can find the equation of a line of regression using your graphic display calculator by doing the following:
STEP 1
Add your raw data to a spreadsheet in your graphic display calculator
- On some models, you must enter it in statistics mode
- The data should be added as two columns
- Label the columns if you are able (e.g. time, length) or x and y
STEP 2
From the statistics function on your graphic display calculator, select the statistics calculations
- Choose the option linear regression $(m x + b)$
- On some models you instead select CALC followed by REG
  - You must also then select X, as we are finding a linear model, rather than quadratic or cubic etc
  - Then select ax+b for the format of the equation
STEP 3
Assign the correct columns into your spreadsheet for the x and y lists
- This is why labelling your columns at the start is important
- Some models may simply assume the first column contains the x values
STEP 4
Write down the values for $m$ and $b$ produced by your calculator
- Round each of the values to 3 significant figures (unless they can be written exactly)
STEP 5
Substitute the values for $m$ and $b$ into the equation $y = m x + b$

How do I use and interpret the equation of a linear regression line?

You may be asked to draw a regression line onto a scatter diagram
- You need to know two points on the line
  - Choose two $x$ values (they don't need to correspond to any data values!)
  - Substitute these into the equation of the regression line to find the corresponding $y$ values
- Plot these two points on the scatter diagram and draw a straight line through them
  - Use a ruler!
A regression line drawn from its equation will always go through the mean point, $(\bar{x}, \bar{y})$ for the data set
- You may be required to use this fact in an exam question

Examiner Tips and Tricks

Be careful with the $y = m x + b$ form of the regression line
- It is the same as the $y = m x + c$ version of a straight line equation but uses the variable $b$ rather than $c$

Worked Example

Rebecca, a regular jogger, recorded the number of calories she was able to burn ( $y$ calories) by running different distances ( $x$ km). This data is shown in the table and on the scatter diagram below.

Distance run (km)	10	2	7	6	12	14	5
Calories burned	620	180	438	366	830	870	315

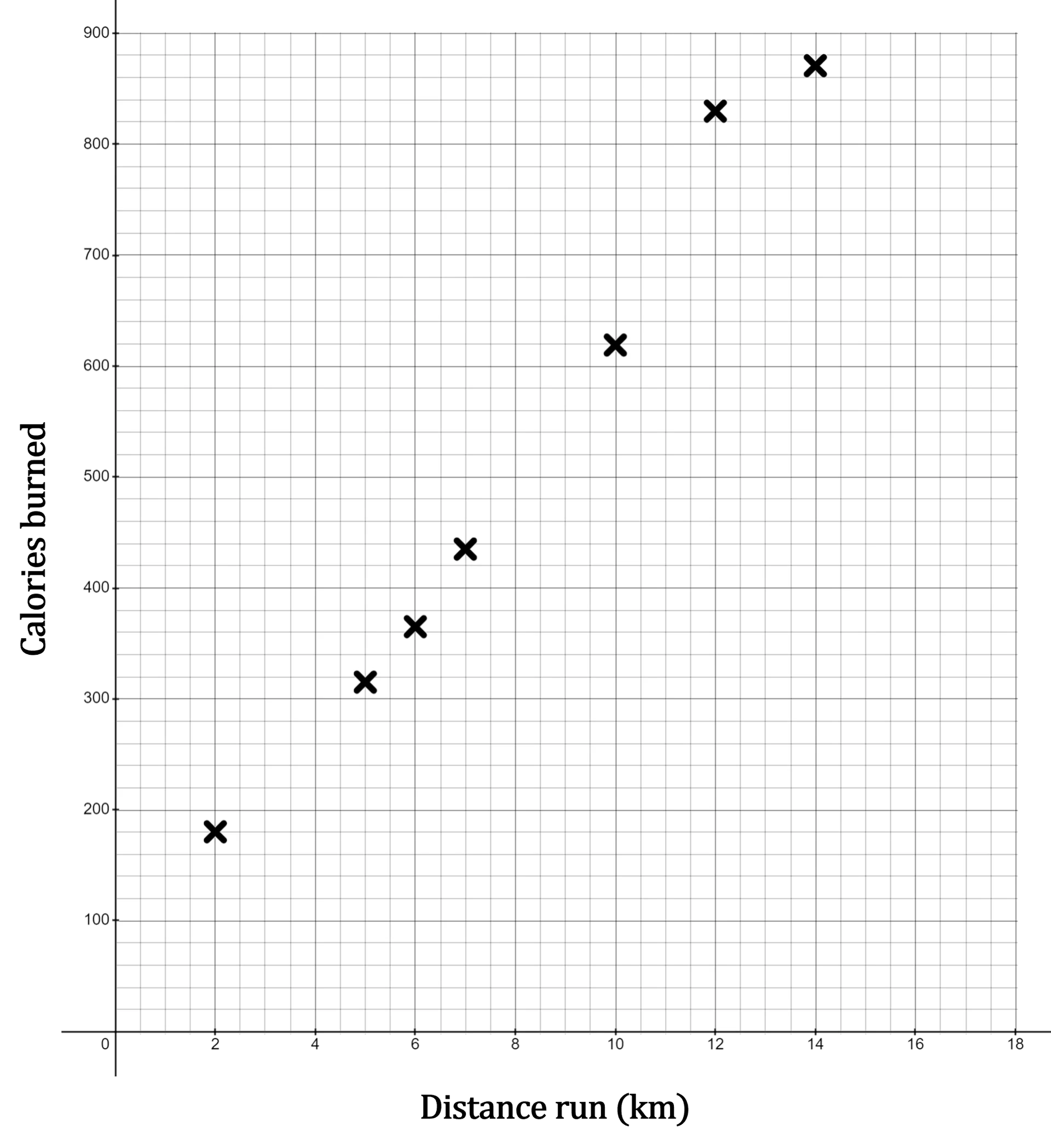
Scatter graph showing data for calories burned against distance run

(a) Find the equation of the regression line for $y$ in terms of $x$ .

Enter the data as two columns in a spreadsheet or statistics mode on your graphic display calculator
Label the columns if you are able to; x (distance run) and y (calories burned)

$x$	$y$
10	620
2	180
7	438
6	366
12	830
14	870
5	315

Select the stats calculation from the statistics function
Choose the option for the linear regression $(m x + b)$
Select the column that you input the distance data as the x list and the column that you input the calories burned data as the y list

On some models you instead select CALC followed by REG, then X for a linear model, and finally select ax+b for the format of the equation

Write down the values for $m$ and $b$ and round to 3 significant figures

$m = 62.12264 . . . \approx 62.1 b = 20.01886 . . . \approx 20.0$

$y = 62.1 x + 20.0$

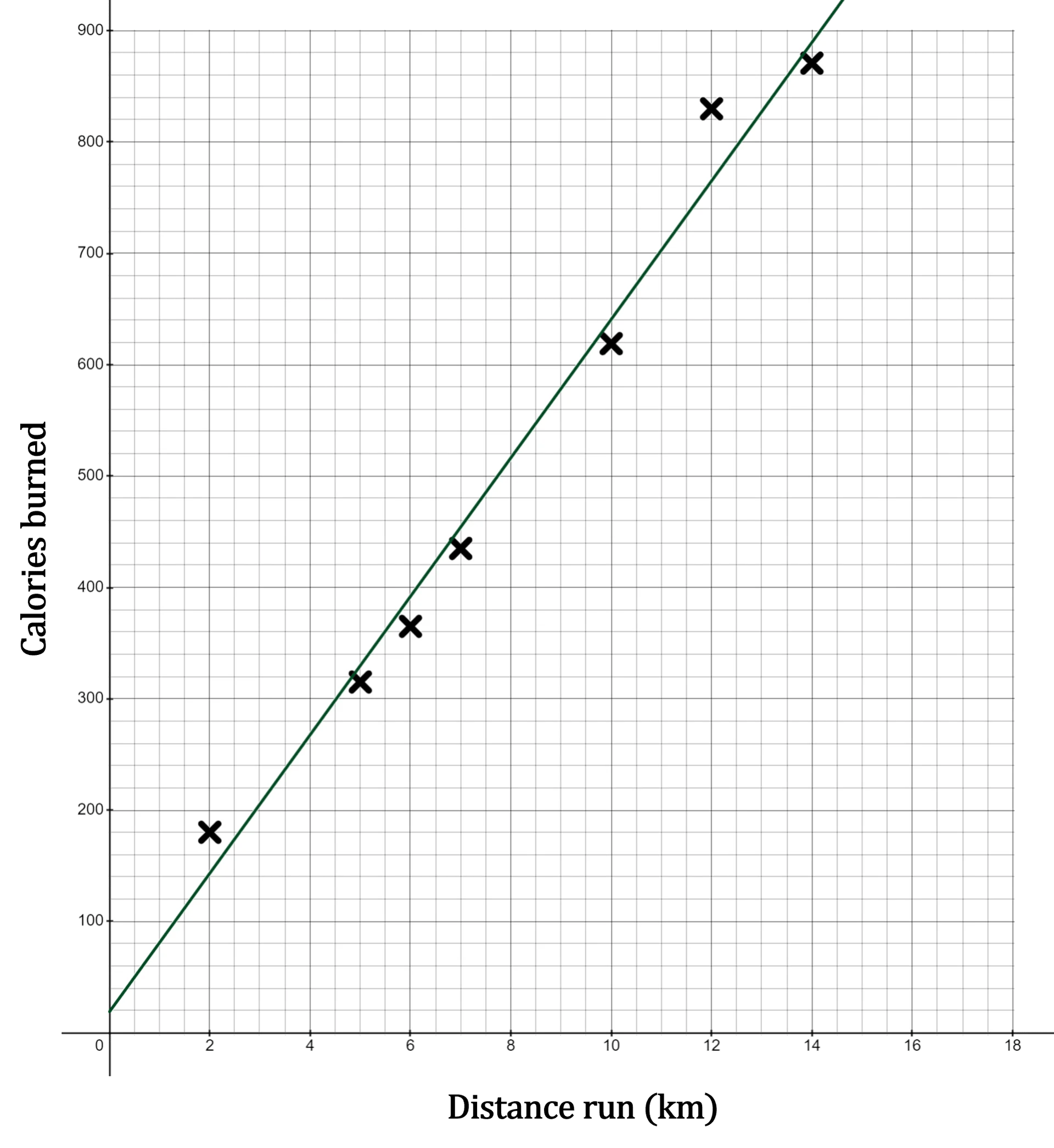
(b) Draw the regression line on the scatter diagram.

Find the coordinates of two points on the line and draw the line through these points

$when x = 0, y = 62.1 (0) + 20.0 = 20.0 when x = 10, y = 62.1 (10) + 20.0 = 641$

So draw the line through the points (0, 20) and (10, 641)

The scatter diagram from the question with the regression line drawn on

The mean of the data values for the distance run is 8 km.

(b) Use this information to find the mean of the data values for the calories burned.

Use the fact that the regression line always goes through the mean point $(\bar{x}, \bar{y})$

Draw a vertical line up from 8 on the x-axis until it hits the regression line
Then draw a horizontal line from there until it hits the y-axis

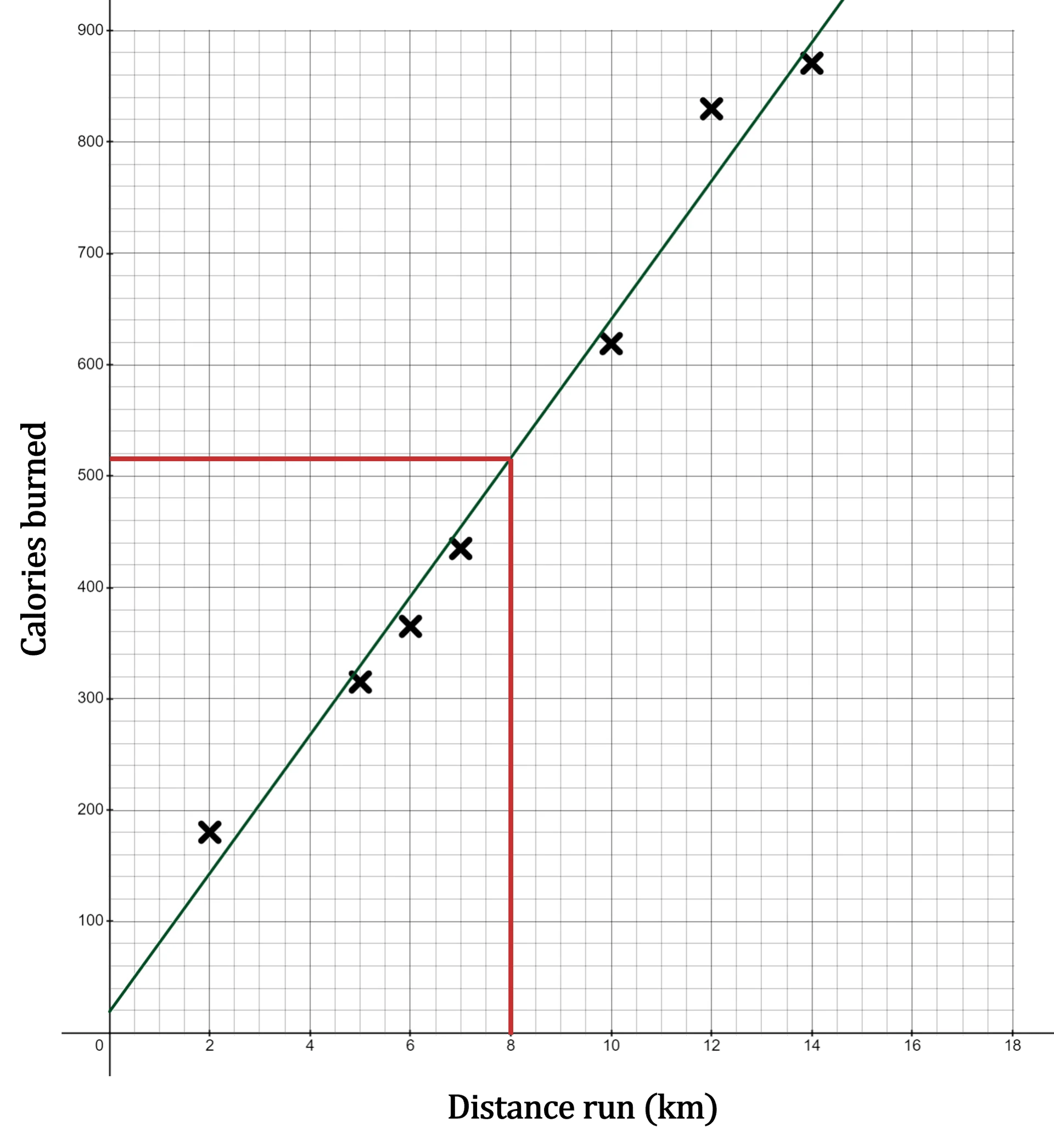
Scatter diagram and regression line, with lines drawn to find the mean of the y values

Read the value off the y-axis (it's a little bit less than 520)

516 calories

Marks would be awarded for a range of answers around that value

Last updated: 12 June 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Lines of Best Fit