Periods & Amplitudes (Cambridge (CIE) IGCSE International Maths)

Revision Note

Written by: Naomi C

Reviewed by: Dan Finlay

Periods & Amplitudes

What are oscillating graphs?

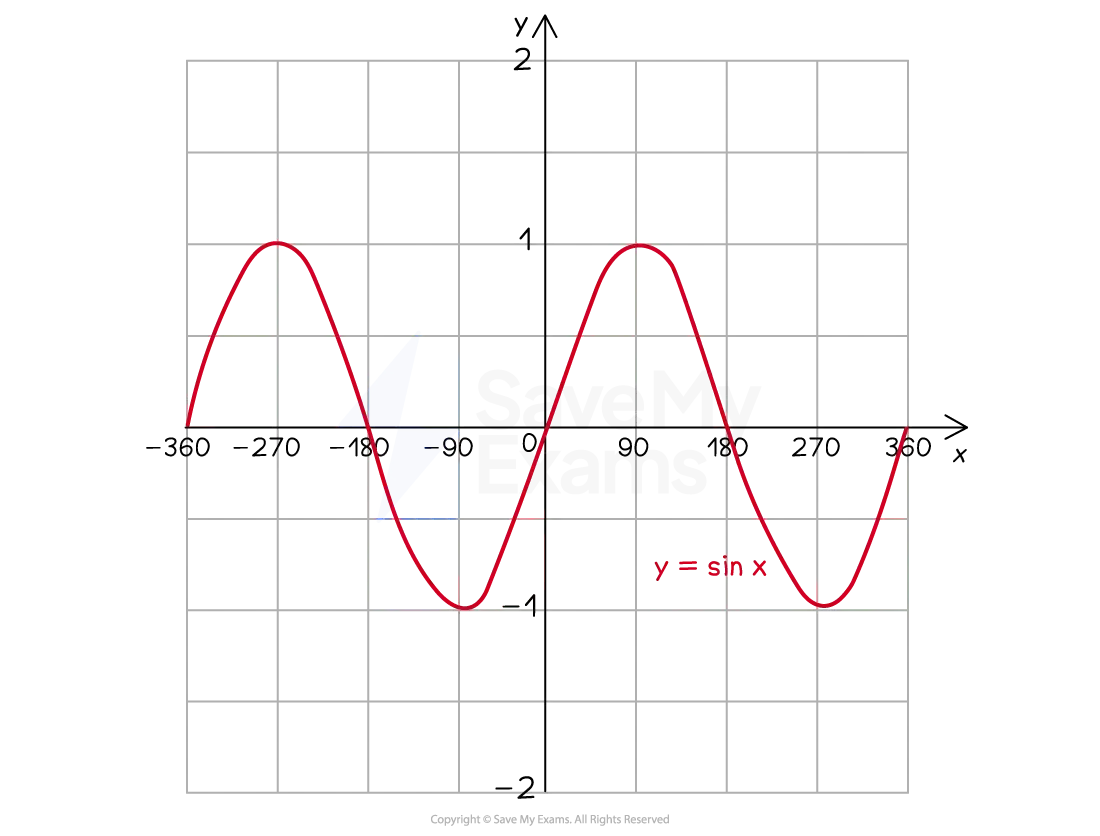
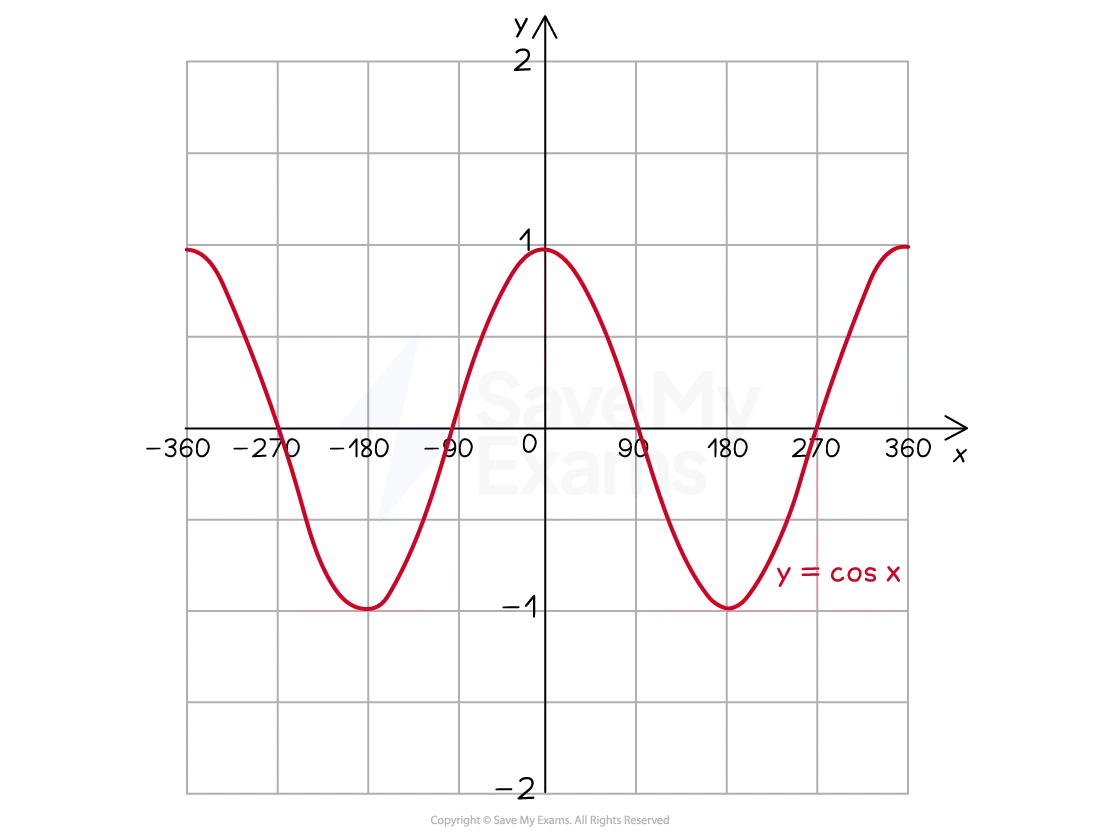
The sine and cosine graphs are oscillating graphs
- Both graphs oscillate between a maximum and a minimum point
- A cycle is completed when the graph returns an initial starting point
- The cycle is repeated indefinitely in both the positive and negative x directions

What are the features of oscillating graphs?

An oscillating graph has the following key features:
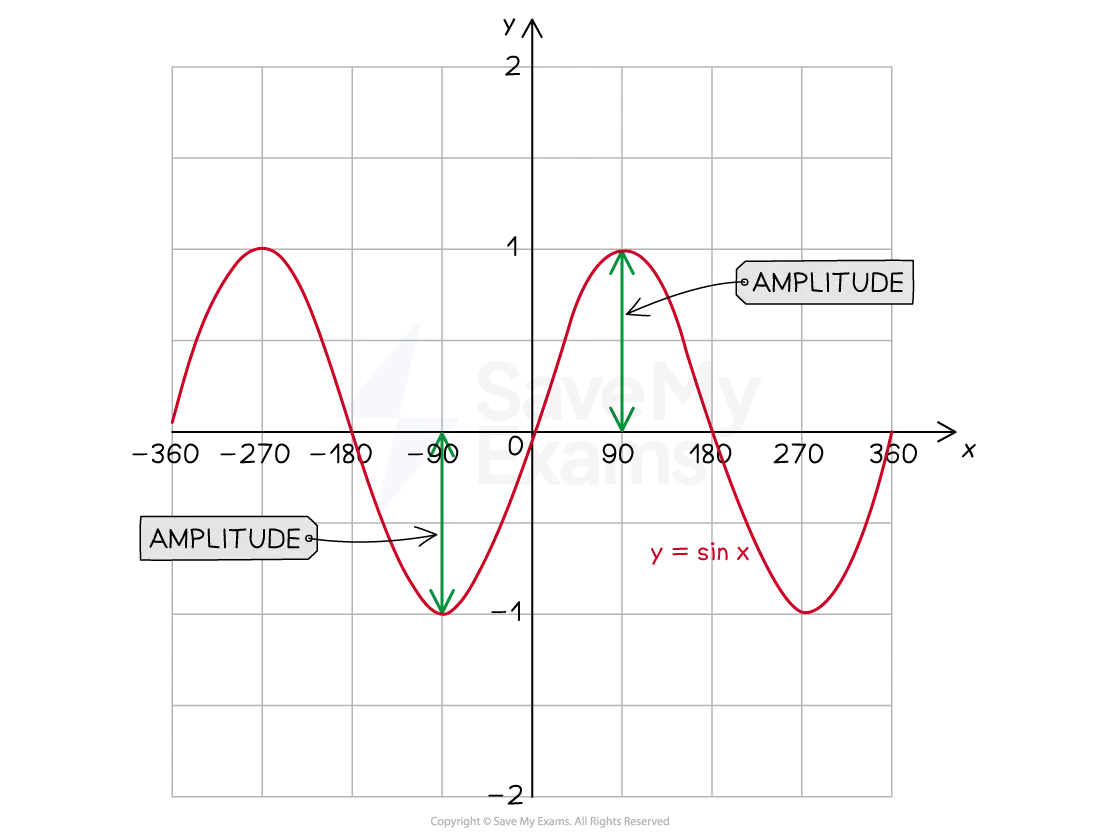
- The amplitude is half the vertical distance from the maximum point to the minimum point
  - This is the distance from the horizontal line of symmetry (often the x-axis) to the minimum or maximum point
- E.g. For the graph $y = \sin x$ the amplitude is 1

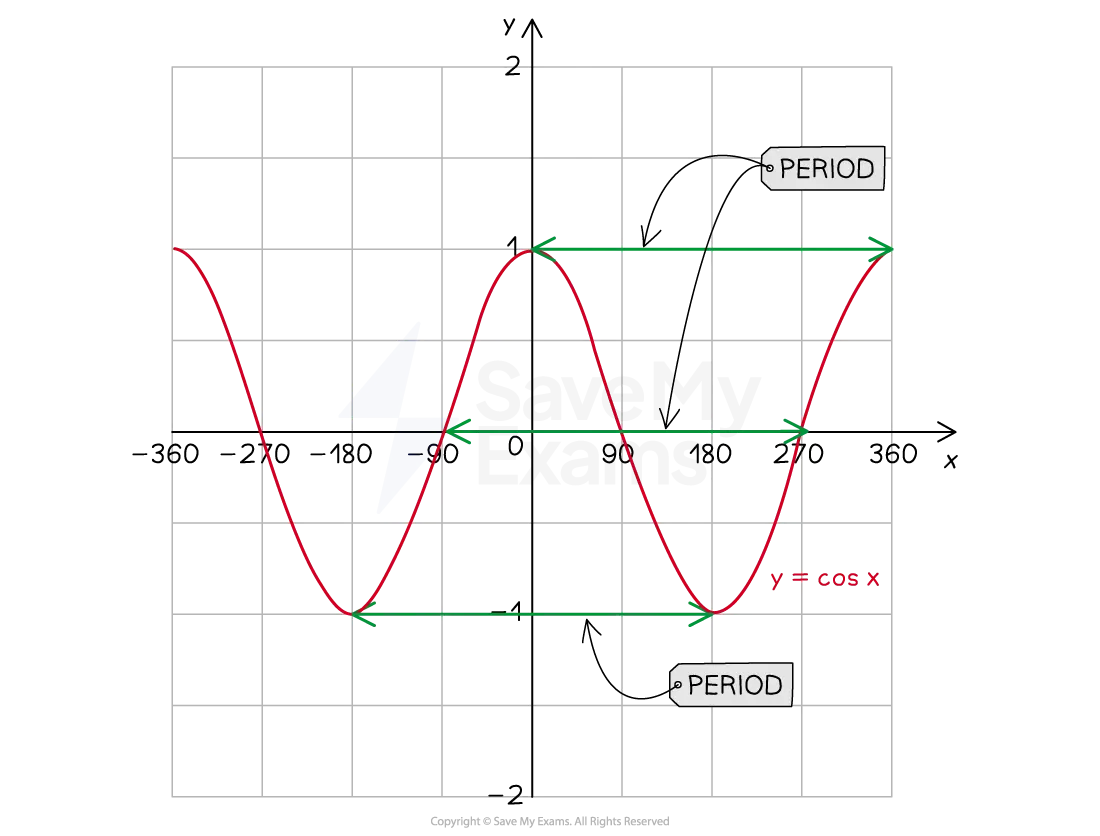
The period is the distance along the x-axis to complete a full oscillation
- Maximum point to maximum point
- Minimum point to minimum point
- x-intercept to next but one x-intercept
- E.g. For the graph $y = \cos x$ the period is 360º

How do I draw an oscillating graph from its equation?

An oscillating function has equation
- $f (x) = a \sin (b x)$
- $f (x) = a \cos (b x)$
The $a$ represents the amplitude of the function
- The bigger the value of $a$ the bigger the range of values of the function
- E.g. For the graph $y = 5 \cos x$
  - The amplitude is 5 units
  - The distance from the x-axis (horizontal line of symmetry) to the maximum/minimum point would be 5 units
- E.g. For the graph $y = 2 + \frac{1}{5} \cos x$
  - The amplitude is $\frac{1}{5}$ of a unit
  - The vertical distance from the line $y = 2$ to the maximum/minimum point would be $\frac{1}{5}$ of a unit
The $b$ determines the period of the function
- The bigger the value of $b$ the quicker the function repeats a cycle
- The period is $\frac{360 °}{b}$
  - A larger value of $b$ produces a shorter period
- E.g. For the graph $y = \sin (2 x)$
  - The period is $\frac{360}{2} = 180 °$
  - The graph has been 'squashed' by a factor of 2 horizontally
  - Two complete cycles will occur in an interval of $360 °$
- E.g. For the graph $y = \sin (\frac{1}{2} x)$
  - The period is $\frac{360}{\frac{1}{2}} = 360 \times \frac{2}{1} = 720 °$
  - The graph has been 'stretched'
  - Half a cycle will occur in an interval of $360 °$

Examiner Tips and Tricks

You can use your graphic display calculator to help you interpret or compare trigonometric graphs

Worked Example

The diagram below shows the graph with equation $y = a \sin (b x)$ , where $a$ and $b$ are integer values.

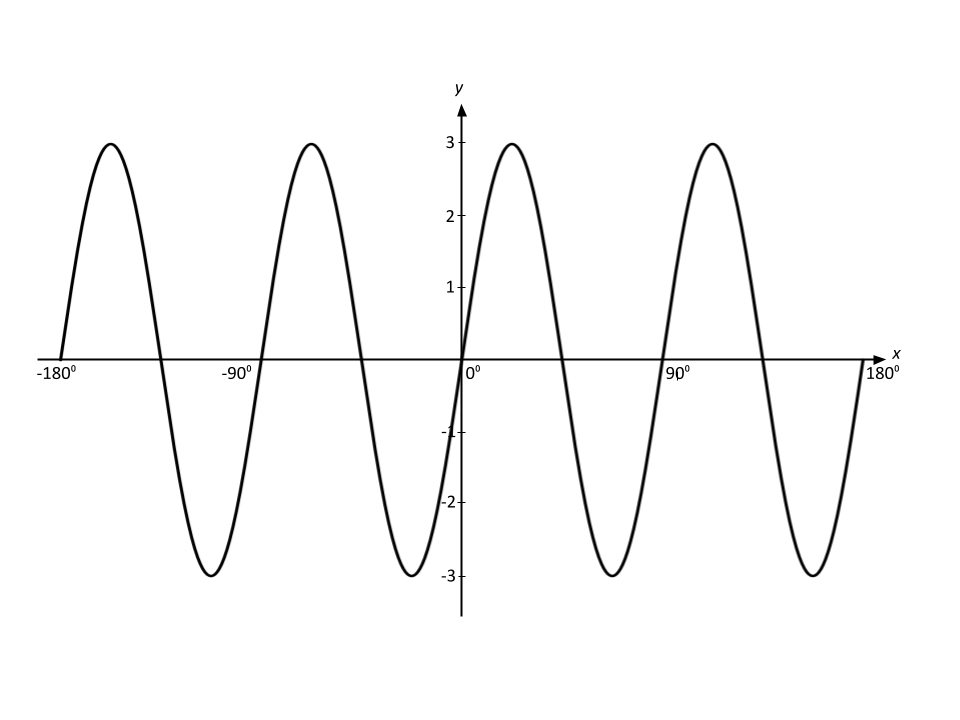
(a) Write down the period.

The graph intersects the x axis at 0, then again at 45º and again at 90º

One full cycle is complete over an interval of 90º

Period = 90º

(b) Write down the amplitude.

The graph goes to a maximum of 3 and a minimum of -3

Amplitude = 3

$a$ is the amplitude

The period is $\frac{360 °}{b}$

$\begin{array}{rcl} 90 & = & \frac{360}{b} \\ b & = & \frac{360}{90} \\ b & = & 4 \end{array}$

$a = 3 b = 4$

(d) Give a reason as to why the picture cannot be modelled by $y = a \cos (b x)$ .

The curve in the diagram goes through the origin $(0, 0)$
but a curve with equation of the form $y = a \cos (b x)$
would intercept the y-axis at $(0, a)$

Any suitable reason as to how a cosine graph is different from a sine graph

Last updated: 15 November 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Trigonometric GraphsNext:Solving Trig Equations