Deciding the Trig Rule (Cambridge (CIE) IGCSE International Maths)

Revision Note

Written by: Amber

Reviewed by: Dan Finlay

Applications of Trigonometry

How do I decide which trig rule to use?

Different rules are required depending on the question
- You need to be able to decide which is appropriate to use
- Think about what information you have and what you want to find
This table summarises the possibilities:

If you know	And you want to know	Use
Two sides and an angle opposite one of the sides	The angle opposite the other side	Sine rule
Two angles and a side opposite one of the angles	The side opposite the other angle	Sine rule
Two sides and the angle between them	The third side	Cosine rule
All three sides	Any angle	Cosine rule
Two sides and the angle between them	The area of the triangle	Area of a triangle rule

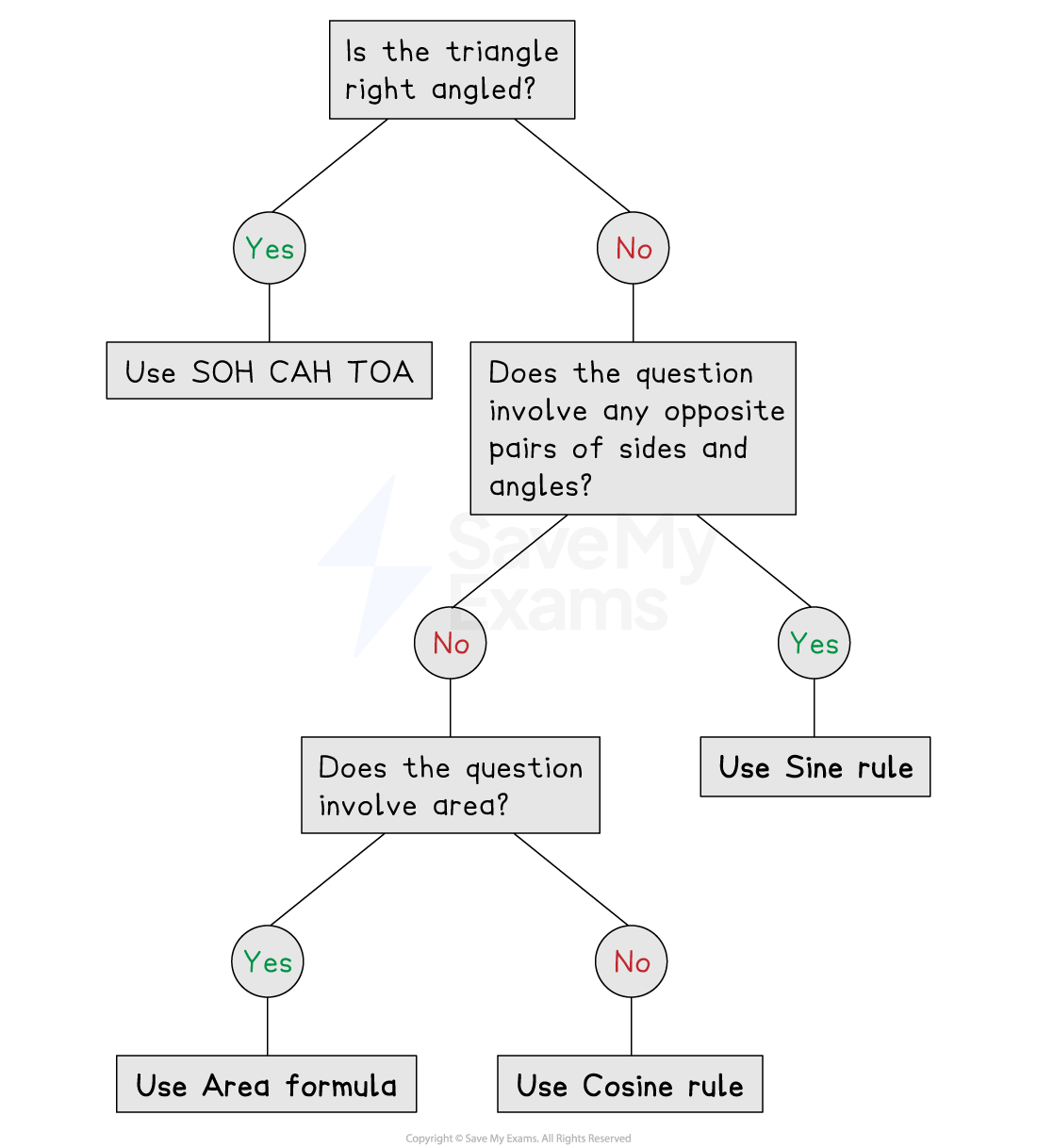
Flow chart to determine which rule or formula to use.

Can I use multiple trig rules in the same question?

Harder questions will require you to use more than one trig rule
- For example, you may need the sine rule followed by the cosine rule
The area formula only works for an angle between two sides
- If you are not given this setup, you may need to use the sine or cosine rule first

If it looks like no rule would work, remember that all angles in a triangle sum to 180
- This often helps to find a missing angle

Examiner Tips and Tricks

Look at the number of marks for a question - if it is a lot, you are likely to need more than one trig rule!

Worked Example

Find the area of the triangle below.

General-Triangle-with-values-2, IGCSE & GCSE Maths revision notes

The area of a triangle can be found using the formula $A = \frac{1}{2} a b \sin C$

The three side lengths are known , but we need to find an angle in order to calculate the area
Because we know all three sides, any of the angles could be found

Find angle ABC using the cosine rule

Cosine Rule: $a^{2} = b^{2} + c^{2} - 2 b c \cos A$ ,
where $A$ is the angle opposite side $a$

$\begin{array}{rcl} A C^{2} & = & A B^{2} + B C^{2} - 2 (A B) (B C) \cos A B C \\ 4 . 4^{2} & = & 7 . 4^{2} + 4 . 8^{2} - 2 (7.4) (4.8) \cos A B C \end{array}$

Rearrange to make $\cos A B C$ the subject

$\begin{array}{rcl} 4 . 4^{2} - (7 . 4^{2} + 4 . 8^{2}) & = & - 2 (7.4) (4.8) \cos A B C \\ \cos A B C & = & \frac{4 . 4^{2} - 7 . 4^{2} - 4 . 8^{2}}{- 2 (7.4) (4.8)} \end{array}$

Use your calculator to find the value of $\cos A B C$

$\begin{array}{rcl} \cos A B C & = & \frac{487}{592} \end{array}$

Use the cos^-1 button on your calculator to find the value of $A B C$

$\begin{array}{rcl} A B C & = & \cos^{- 1} (\frac{487}{592}) \\ = & 34.65054 . . . \end{array}$

Now we can find the area of the triangle using the formula and angle ABC as the known angle

$\begin{array}{rcl} Area & = & \frac{1}{2} \times 4.8 \times 7.4 \times \sin 34.65054 . . . \\ = & 10.09779 . . . \end{array}$

$Area = 10.1 {cm}^{2} (3 s . f .)$

Last updated: 4 June 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Area of a TriangleNext:3D Pythagoras & Trigonometry