Problem Solving with Volumes (Cambridge (CIE) IGCSE International Maths): Revision Note
Exam code: 0607
Problem-solving with volumes
What is problem-solving?
Problem-solving, usually has two key features:
A question is given as a real-life scenario
eg. The volume of water in a swimming pool...
There is usually more than one topic of maths you will need in order to answer the question
eg. Volume and money
What are common problems that involve volume?
Volume is a commonly used topic of 'real-world' maths
For example, a carton of juice in the shape of a cuboid, a cylindrical tin and a triangular prism chocolate box all involve volume
Typically, the 'real-world' scenarios also have a cost
A lot of volume problems also involve calculations with money
How do I solve problems involving volume?
Often the 3D object in a question will not be a standard cuboid, cone, sphere, etc.
It will likely either be:
A prism (3D shape with the same cross-section running through it)
A portion or fraction of a standard shape (a hemisphere for example)
A compound object (an object made up of two or more standard 3D objects)
If the object is a prism, recall that the volume of a prism is the cross-sectional area × its length
The cross-sectional area may be a compound 2D shape
For example, an L-shape, or a combination of a rectangle and a triangle
If the object is a fraction of a standard shape, consider the "full" version of the object and find the appropriate fraction of it
A hemisphere is half a sphere
A frustum is a truncated (chopped-off) cone or pyramid
The volume of a frustum will be the volume of the smaller cone or pyramid subtracted from the volume of the larger cone or pyramid
If the object is a compound object, find the volumes of the individual standard 3D objects and add them together
Problem solving questions could appear on either a non-calculator paper or a calculator paper
Examiner Tips and Tricks
Before you start calculating, make a quick note of your plan to tackle the question.
For example, "Find the area of the triangle and the rectangle, add together, multiply by the length".
Worked Example
The diagram shows a prism.
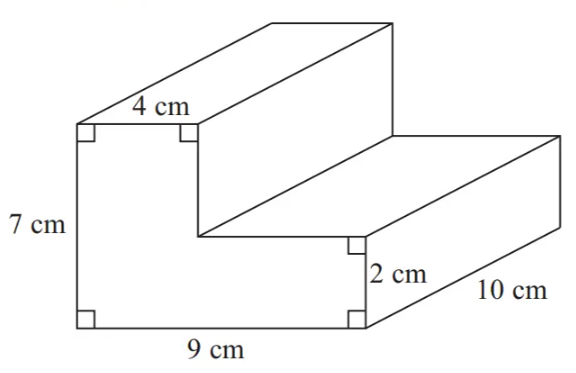
Work out the volume of the prism.
Answer:
The volume is the area of the cross section × length (10 cm)
Find the area by splitting into a 7 × 4 and a (9 - 4) × 2 rectangle (or a 9 × 2 and a (7 - 2) × 4 rectangle)
7 × 4 + (9 - 4) × 2 = 38 cm2
Find the volume (by multiplying 38 by 10)
38 × 10
380 cm3
Worked Example
The diagram shows a truncated cone (a frustum).
Using the given dimensions, find the volume of the frustum to 3 significant figures.
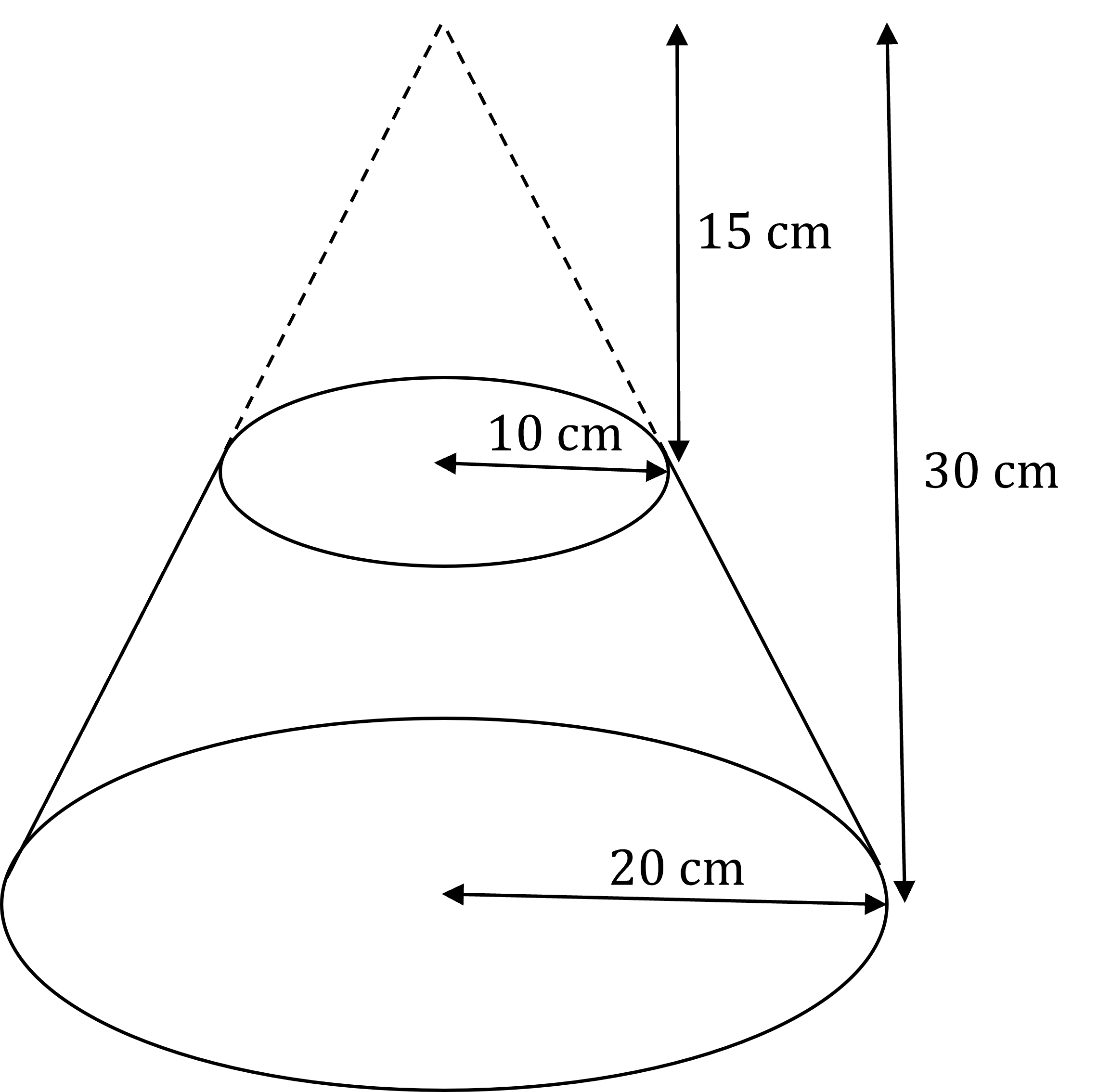
Answer:
To find the volume of the frustum, find the volume of the larger cone (30 cm tall, with a radius of 20 cm), and subtract the volume of the smaller cone (15 cm tall, with a radius of 10 cm)
Formula for the volume of a cone:
Calculate the volume of the larger cone
Calculate the volume of the smaller cone
Find the difference
Round to 3 significant figures
11 000 cm3

Unlock more, it's free!
Did this page help you?