Angles in the Same Segment (Cambridge (CIE) IGCSE International Maths)
Revision Note
Written by: Amber
Reviewed by: Dan Finlay
Did this video help you?
Circles & Segments
Circle Theorem: Angles in the same segment are equal
Any two angles on the circumference of a circle that are formed from the same two points on the circumference are equal
These two angles are in the same segment of the circle
To see this, add the chord PQ below to split the circle into two segments
To spot this circle theorem on a diagram
Find two points on the circumference that meet at a third point
See if there are any other pairs of lines from the same two original points that meet at a different point on the circumference
When explaining this theorem in an exam you must use the keywords:
Angles in the same segment are equal
Look out for a bowtie shape
The theorem works upside down, in that the angles at P and Q are also equal
Examiner Tips and Tricks
An exam question diagram may have multiple equal angles
Look for as many as possible by seeing how many pairs of lines start from the same two points on the circumference
Worked Example
The diagram below shows a circle with centre, O.
A, B, C, D and E are five points on the circumference on the circle.
Angle AEB = 12º.
Angle BEC = 14º.
Angle CED = 73º.
Angle EBD = θº.
Find the value of θ .
CE is a diameter
This means that triangles EAC and CED are both triangles in a semicircle
Angle EAC = 90º
Angle CED = 90º
Angle in a semicircle = 90º
Find the other angles in the triangles
Angle ECA = 64º
Angle ECD = 17º
Angles in a triangle = 180º
Label these angles on the diagram
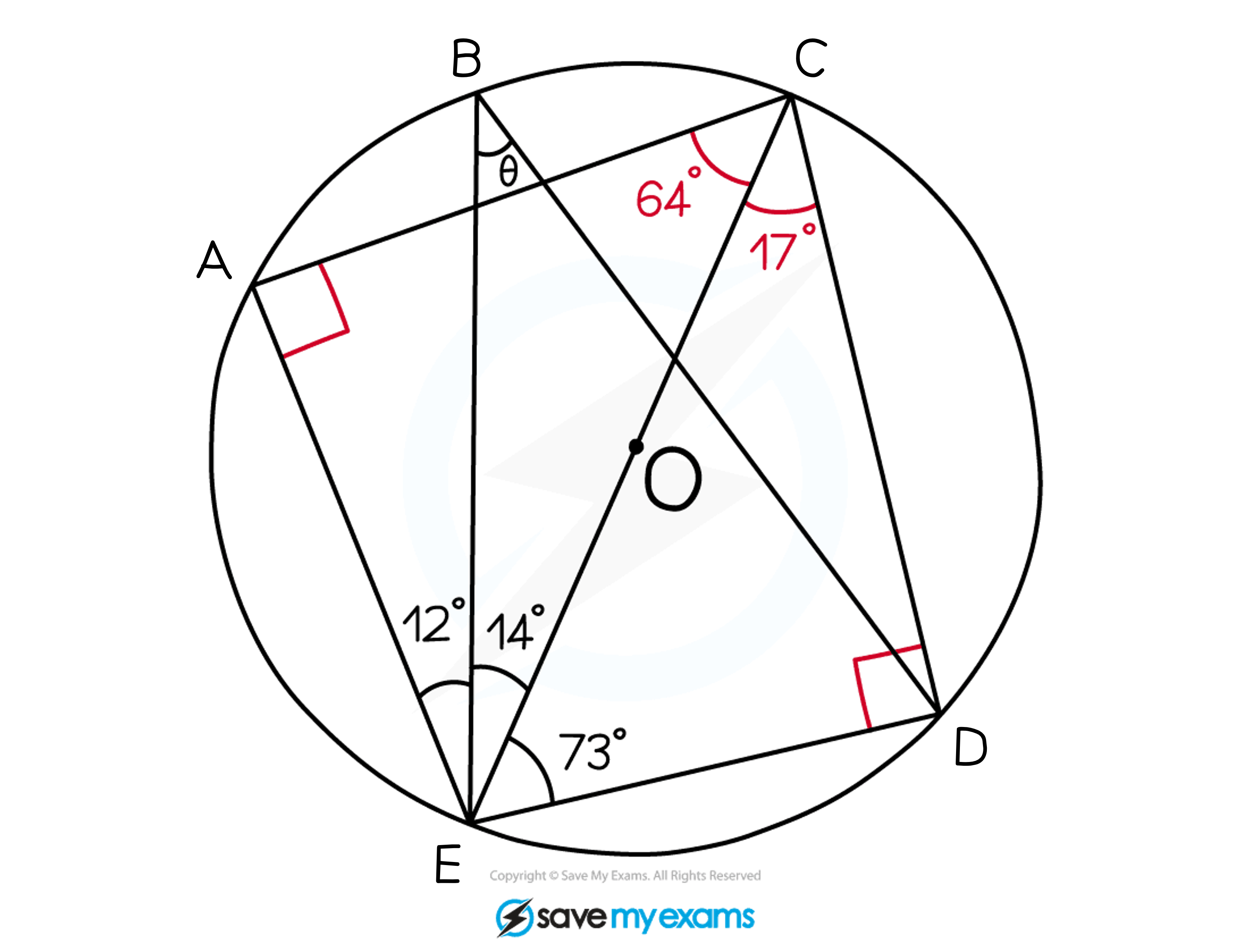
Angle θ is formed by two lines coming from either end of the chord ED
Angle ECD is also formed by two lines coming from either end of the chord ED
Angle θ = angle ECD = 17º
Angles in the same segment are equal
Angle θ = 17º
Last updated:
You've read 0 of your 10 free revision notes
Unlock more, it's free!
Did this page help you?
