Angles at Centre & Circumference (Cambridge (CIE) IGCSE International Maths)

Angles at Centre & Circumference

What are circle theorems?

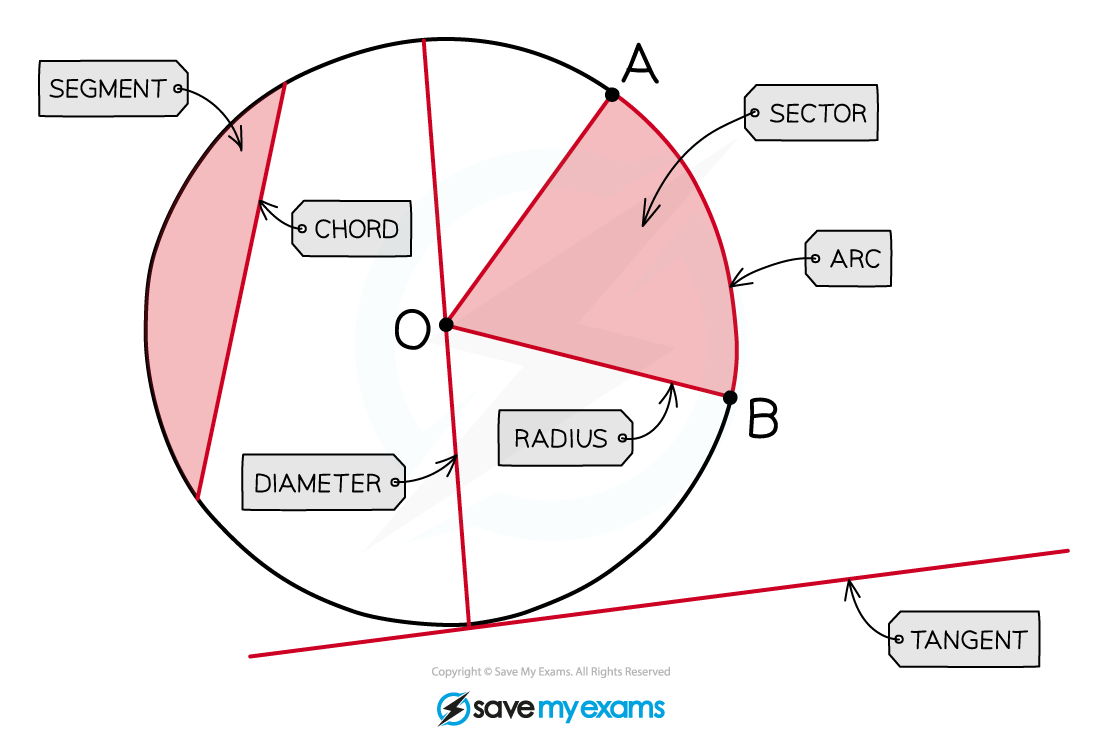
• Circle Theorems deal with angles that occur when lines are drawn within (and connected to) a circle

• You may need to use other facts and rules such as:

  • basic properties of lines and angles

  • properties of triangles and quadrilaterals

  • angles in parallel lines or polygons

Circle Theorem: The angle at the centre is twice the angle at the circumference

• In this theorem, the chords (radii) to the centre and the chords to the circumference are both drawn from (subtended by) the ends of the same arc

• To spot this circle theorem on a diagram

  • find any two radii in the circle and follow them to the circumference

  • see if there are lines from those points going to any other point on the circumference

  • it may look like the shape of an arrowhead

• When explaining this theorem in an exam you must use the keywords:

  • The angle at the centre is twice the angle at the circumference

• This theorem is still true when the ‘triangle parts’ overlap

  

• It is also true when the lines form a diamond shape

  • You need to compare the reflex angle at the centre with the angle at the circumference

  • Common mistakes are to

    • compare the wrong angles

    • confuse it with a different circle theorem on cyclic quadrilaterals