Using Calculators to Sketch Graphs (Cambridge (CIE) IGCSE International Maths)

Revision Note

Written by: Mark Curtis

Reviewed by: Dan Finlay

Using Calculators to Sketch Graphs

How do I draw graphs on my graphic display calculator?

Navigate on your calculator to the Add Graphs button
- You may need to start a new document first
- On some models you will need to select graph mode in the menu
Enter the equation of the function on the line f(x)=
- This is the function, $f (x)$
- On other models it may be labelled as f1(x)= or Y1:
Press enter or EXE and the graph should appear
- You may need to go to the menu or press the zoom button to zoom in or out
  - The "zoom - fit" button (or equivalent) automatically zooms for you on the key features
  - Other models may also have a "V-Window" menu where you can select the exact range of values to show

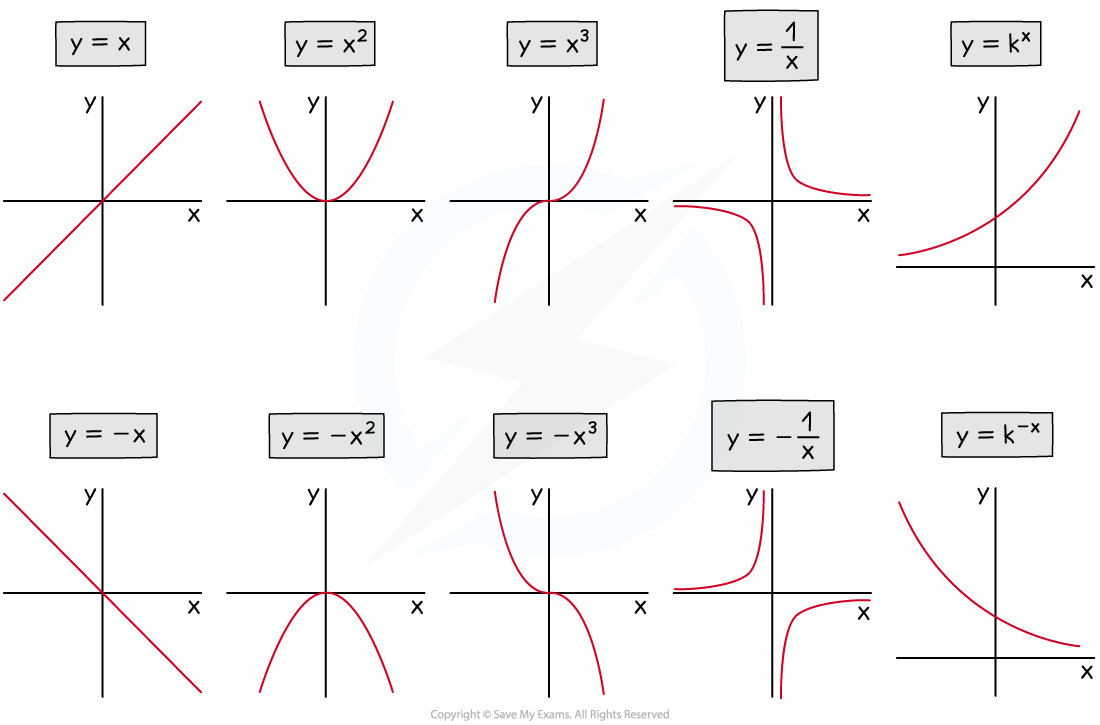
Examples of linear, quadratic, cubic, reciprocal, and exponential graphs

How do I find graph features using my graphic display calculator?

Once the graph is drawn, go to the menu and select analyze graph (or equivalent), which gives a list of options
- Other models may feature a G-Solv button
Zeros (or roots): these are the x-intercepts
- You may have to click before and after the x-intercept you require so that the calculator knows where to search
- y-intercepts can be found without a calculator by substituting $x = 0$ into $f (x)$
  - though some models do include a Y-ICEPT button which can be used
Maximum or minimum points: these are the coordinates of the highest point and lowest point on the graph
- You may have to click before and after the point you require so that the calculator knows where to search
- These can be called local maxima or local minima
- They are also referred to as turning points
  - or the vertex if talking about a quadratic graph

positive and negative quadratics with maximum and minimum points labelled respectively

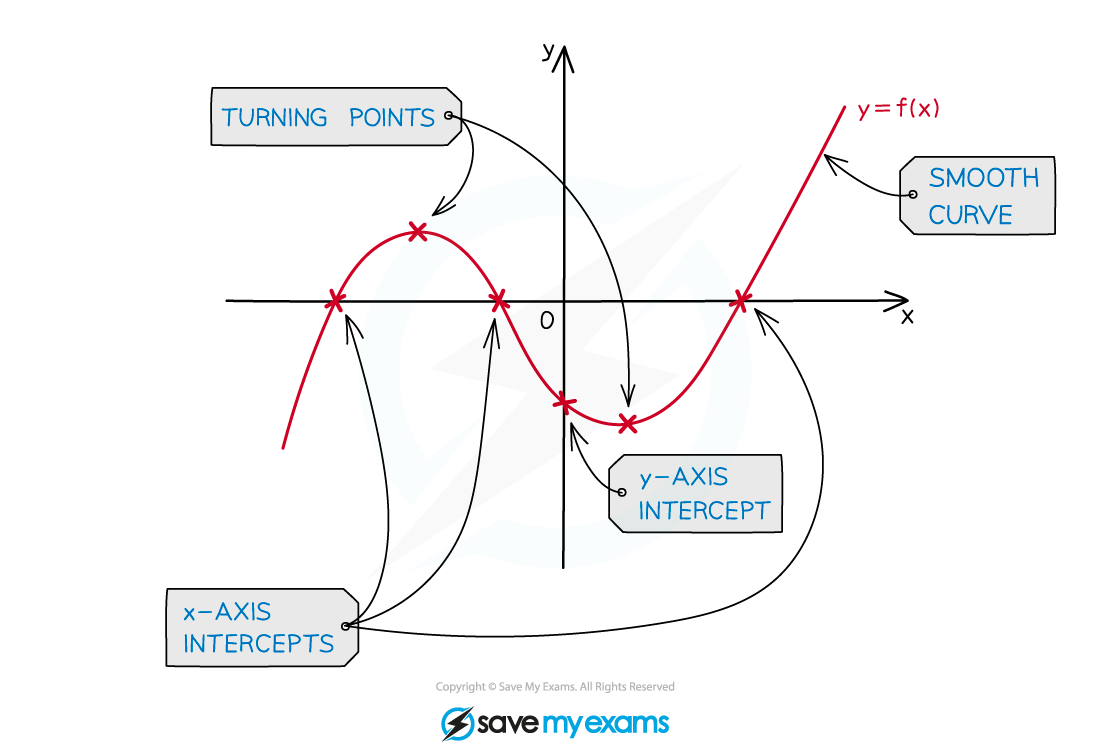
positive cubic with turning points, roots, y intercept, all labelled

How do I sketch a graph in the exam from my graphic display calculator?

Exam questions may ask you to sketch the graph on a given blank set of axes
- You do not need to plot points exactly
  - and you do not need a table of values
- Draw a single smooth freehand curve that copies the shape of the curve on your graphic display calculator
  - Do not use a ruler for curves!
  - Copy any key features and symmetries

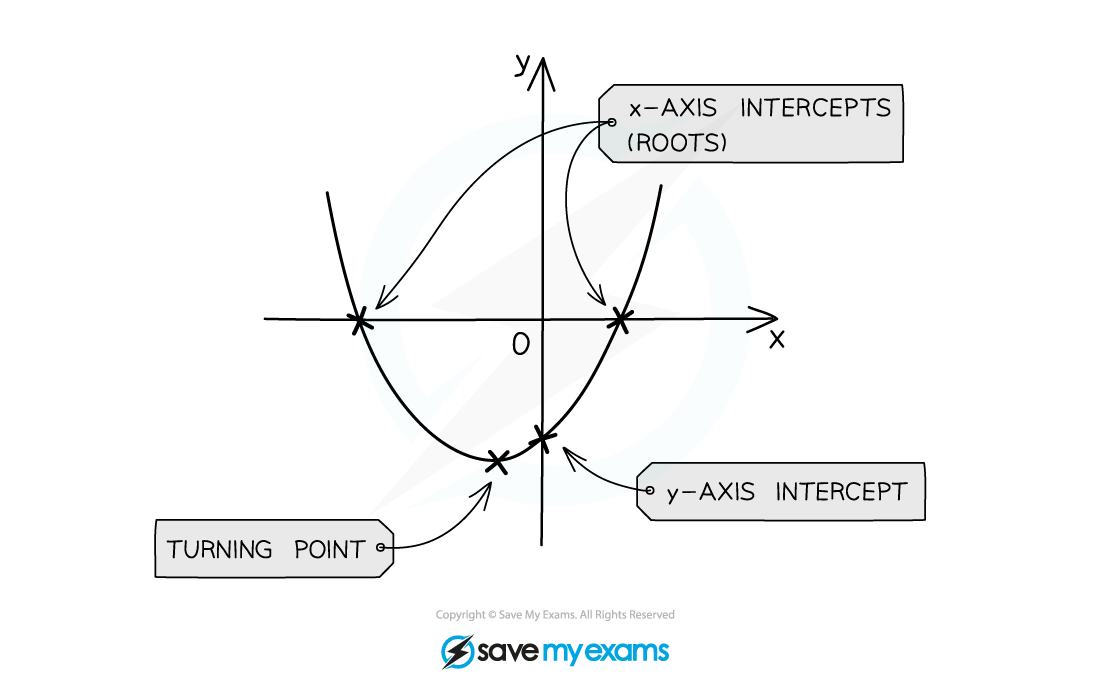
Quadratic graph with roots, turning point, and y-intercept labelled

Exam questions may ask you to use your calculator to sketch an unknown function that you have not seen before

How do I create a table of values on my graphic display calculator?

Your calculator can create tables of values for you, if needed
Find the table function
- Type in the graph equation (the function, f(x)=)
- Enter the start value (or equivalent)
  - The first x-value in the table
- Enter the end value (or equivalent)
  - The last x-value in the table
- Enter the step size (or equivalent)
  - How big the steps (gaps) are from one x-value to the next
- You may have to select SET to set the above values
- Press enter or EXE to see the table of values

Examiner Tips and Tricks

Exam questions will say "draw this graph on your calculator" to make it clear when using a calculator is intended

Worked Example

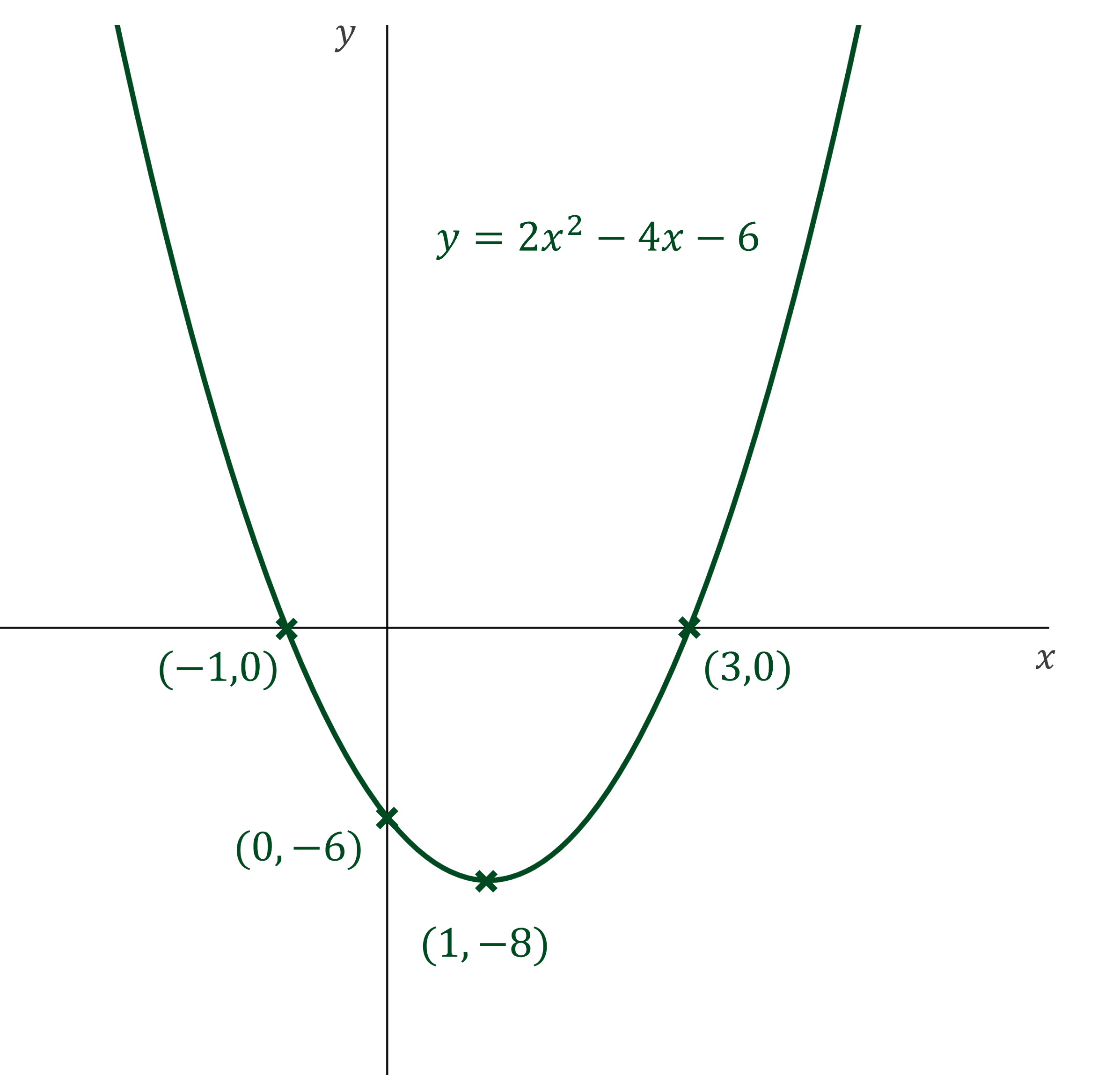
(a) Draw the graph of $y = 2 x^{2} - 4 x - 6$ on your calculator and use it to sketch the curve on the axes provided, showing coordinates of all axes intercepts and any maximum or minimum points.

Start a new graph on your calculator and enter $f (x) = 2 x^{2} - 4 x - 6$ to generate the graph
This shows the curve has a minimum point (not a maximum point)

Select the option to "analyze" the graph (this may be labelled as G-Solv)
Choose the option "zeros" (or roots) to find the x-intercepts
Choose the option "minimum" (or equivalent) to find the coordinates of the minimum point

The question asks for all axes intercepts, so this includes the y-intercept
Substitute $x = 0$ into $f (x) = 2 x^{2} - 4 x - 6$ to get -6
(or you can use the Y-ICEPT button on some models)

Show all the above information on a sketch using coordinates

graph of y=2x^2 - 4x -6 showing roots at (-1,0) and (3,0), y intercept at (0,-6), and minimum point at (1,-8)

(b) Match the following curve equations to the sketches below. You may use your graphic display calculator in this question.

(1) $y = 0.6 x + 2$ (2) $y = 3^{x}$ (3) $y = - 0.7 x^{3}$ (4) $y = \frac{4}{x}$ (5) $y = - x^{2} + 3 x + 2$

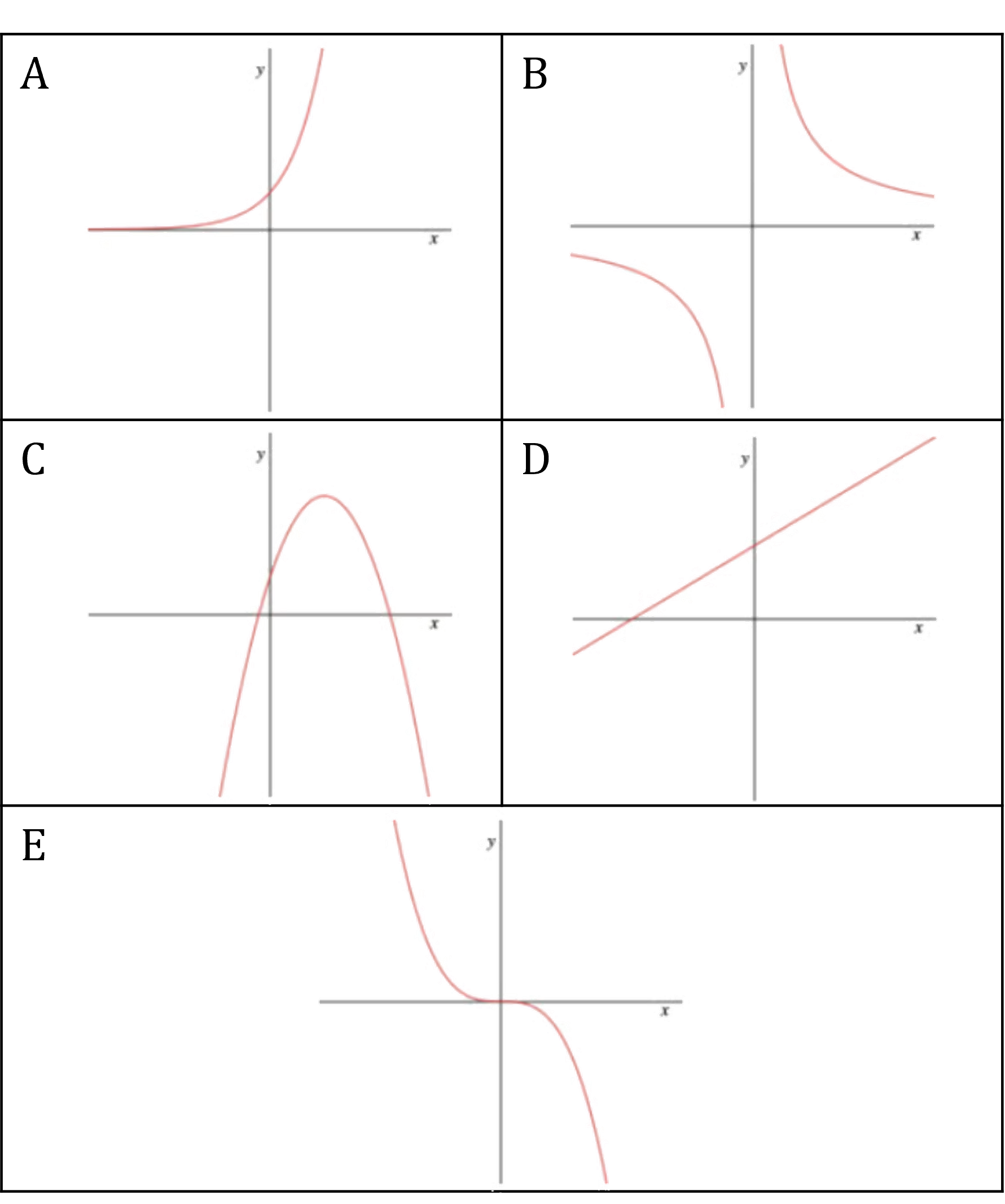
5 different shapes of graph; exponential, reciprocal, negative quadratic, linear, and negative cubic

(1) is a straight line equation (y = mx + c) so must match graph D

(2) requires plotting on a graphic display calculator to see that it is A

(3) requires plotting on a graphic display calculator to see that it is E

(4) requires plotting on a graphic display calculator to see that it is B

(5) is a quadratic equation with a negative coefficient so matches graph C

When plotting these graphs on your calculator, you may need to use the zoom function or V-Window button to see the overall shapes of the graphs

(1) → D
(2) → A
(3) → E
(4) → B
(5) → C

Last updated: 10 June 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Exponential GraphsNext:Using Calculators to Solve Equations