Quadratic Simultaneous Equations (Cambridge (CIE) IGCSE International Maths): Revision Note
Exam code: 0607
Did this video help you?
Quadratic simultaneous equations
What are quadratic simultaneous equations?
When there are two unknowns (e.g. x and y) in a problem, we need two equations to be able to find them both; these are called simultaneous equations
If there is an x2 or y2 or xy in one of the equations then they are quadratic (or non-linear) simultaneous equations
How do I use a graph to solve quadratic simultaneous equations?
Plot both equations on the same set of axes
To do this, you can use a table of values
Or for straight lines it can help to rearrange into y = mx + c
Find the point where the lines intersect
The x and y solutions to the simultaneous equations are the x and y coordinates of the point of intersection
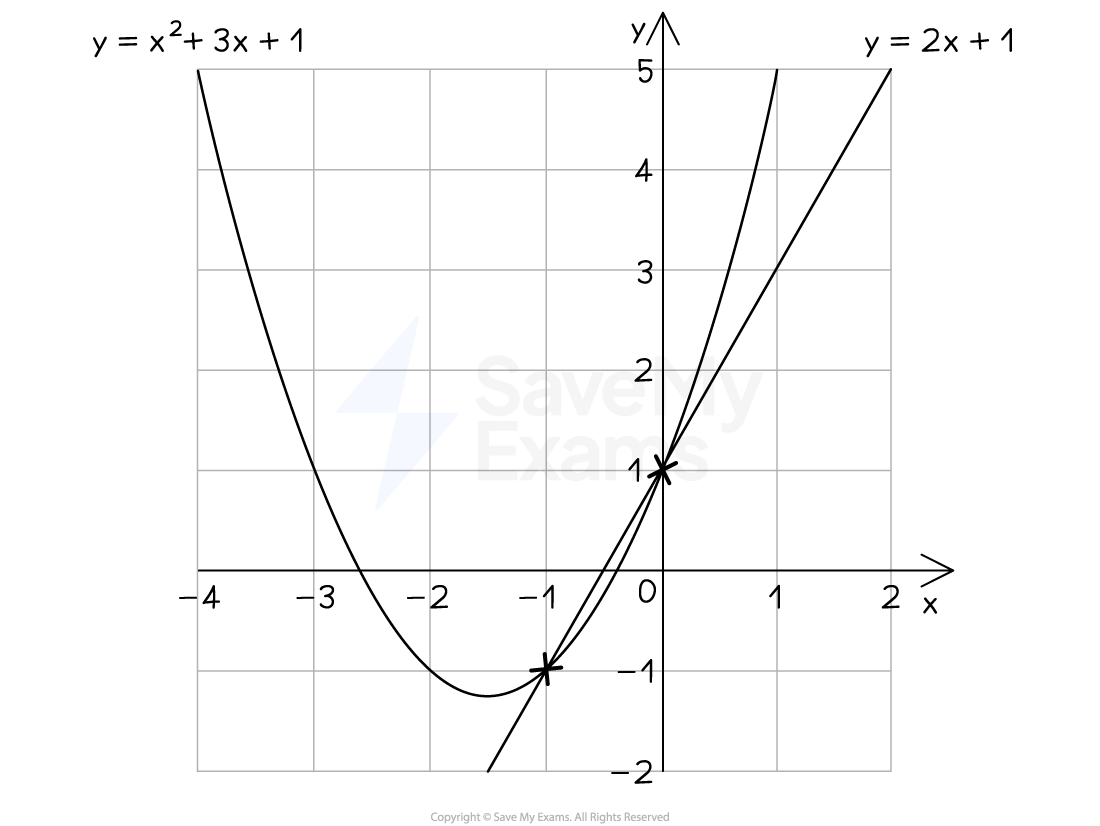
E.g. To solve y = x2 + 3x + 1 and y = 2x + 1 simultaneously
First plot them both (see graph below)
Then find the points of intersection, (-1, -1) and (0, 1)
So the solutions are x = -1 and y = -1 or x = 0 and y = 1
How do I solve quadratic simultaneous equations using algebra?
Use substitution
Substitute the linear equation, y = ... (or x = ...), into the quadratic equation
Do not try to substitute the quadratic equation into the linear equation
E.g. To solve
and
Rearrange the linear equation into
Substitute this into the quadratic equation, replacing all y's with
Expand and solve this quadratic equation
and
Substitute each value of x into the linear equation,
, to find the corresponding y values
Present your solutions in a way that makes it obvious which x belongs to which y
x = 0, y = 5 or x = -4, y = -3
Check your final solutions satisfy both equations
What if the quadratic has repeated roots or no roots?
If the resulting quadratic after substituting has a repeated root,
then the line is a tangent to the curve
i.e. the curve and the line intersect in one place only
There is only one solution for x and y
If the resulting quadratic to be solved has no roots,
then the line does not intersect with the curve
There are no solutions to the simultaneous equations
If this happens it may be an indicator that your working is wrong!
What if I can't substitute one equation into the other straight away?
If the linear equation is not in the form y = ... or x = ...
You will need to rearrange it first, so that it can be substituted into the quadratic equation
Consider solving
and
Either:
Rearrange the second equation to
and substitute into
Expanding produces a quadratic that can be solved for
Or rearrange the first equation to
and substitute into
Multiplying both sides by
produces a quadratic that can be solved for
Examiner Tips and Tricks
When giving your final answer, make sure you indicate which x and y values go together.
Worked Example
Solve the equations
Answer:
Number the equations
There is one quadratic equation and one linear equation so this must be done by substitution
Equation 2 can be rearranged to make the subject, which can then be substituted into equation 1
You could rearrange to make the subject instead, but this results in a fraction which can be more tricky to deal with
Rearranging equation 2
Substituting into equation 1
Expand the brackets
Remember that a bracket squared should be treated the same as double brackets
Simplify
Rearrange to form a quadratic equation that is equal to zero
Do this by subtracting 36 from both sides
Take out the common factor of
Solve to find the values of by equating each factor to zero
or
Solve the linear equation above
So the two values are
Substitute the values of into one of the equations (the linear equation is easiest) to find the values of
Write the final solutions in clear pairs

Unlock more, it's free!
Was this revision note helpful?
