Revision NotesPast Papers
IGCSEMathsCambridge (CIE)International MathsExtendedRevision NotesAlgebra & SequencesProportionVariation Models

Variation Models (Cambridge (CIE) IGCSE International Maths)

Revision Note

Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Variation Models

What is a variation model?

  • A variation, or proportion, model describes how one quantity varies with another

  • For example:

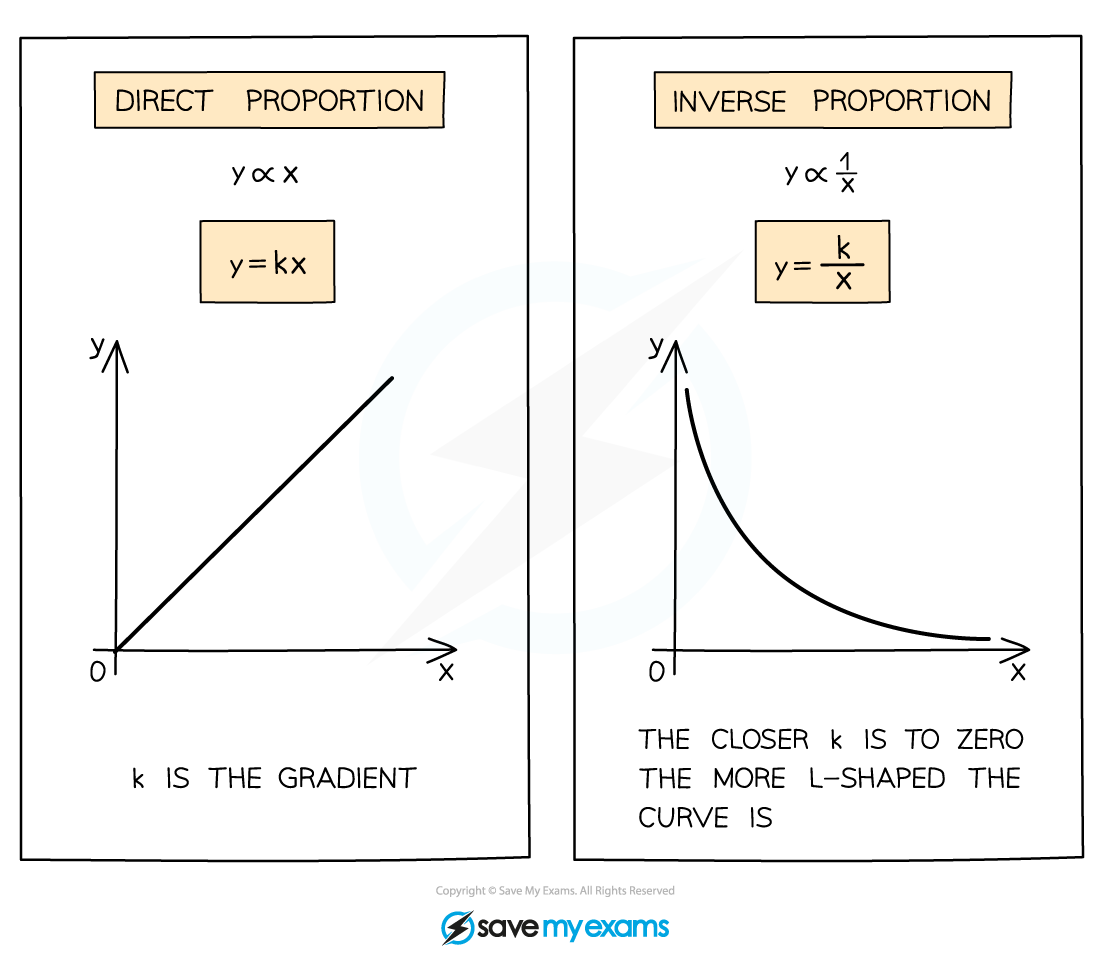
    • y equals k x is a linear variation model and shows direct proportion

    • y equals k x squared is a quadratic variation model

    • y equals k x cubed is a cubic variation model

    • y equals k over x is a reciprocal variation model and shows inverse proportion

Straight line graph of y=kx showing direct proportion, and a reciprocal graph showing y=k/x for inverse proportion

How do I use a variation model to find missing data values?

  • The equation of a variation model is an equation of a curve or line that models a set of data

    • Substitute in the x-values to find the y-values (or the other way around)

  • If you are not given the equation, you may have to find it using the data given

    • E.g. If you are told the model is linear, you can substitute a known pair of x and y values into y equals k x to find k

    • You can then use the full equation to find any missing values

Worked Example

Consider the following table of data.

x

1

3

q

y

36

p

9

Given that y is inversely proportional to x, find the values of p and q.

As y is inversely proportional to x we can write the equation

y equals k over x

Substitute the pair of known values into the equation to find k

table row 36 equals cell k over 1 end cell row k equals 36 end table

So the full equation of the variation model is

y equals 36 over x

Substitute in x equals 3 to find p

p equals 36 over 3 equals 12

bold italic p bold equals bold 12

Substitute in y equals 9 to find q

table row 9 equals cell 36 over q end cell row cell 9 q end cell equals 36 row q equals cell 36 over 9 equals 4 end cell end table

bold italic q bold equals bold 4

How do I identify the best variation model for given data?

  • You may be asked to select the most suitable variation model for given data

  • Using the data to sketch a rough graph is one way to do this

    • You could do this on your graphic display calculator

      • E.g. a U-shaped graph could suggest a quadratic variation model, y equals k x squared

  • If you are given a suggested variation model (or must choose the most suitable from several) you should test the values using the given data

    • Substitute the value of x into the suggested model, and see how close the result is to the actual value of y in the table

    • Do this for at least 3 data points

    • You will then be able to judge if the suggested model is appropriate, or select the best one

Worked Example

Consider the data in the table below.
Decide which out of a linear, quadratic, or cubic variation model would be most suitable for the data, and use this to find an equation for y in terms of x.

x

2

4

6

y

20

80

180

Start by checking if the model is linear, y equals k x

Using the first data point to find k

table row 20 equals cell k cross times 2 end cell row k equals 10 end table

Use this to check the second data point

y equals 10 x y equals 10 open parentheses 4 close parentheses equals 40

Not close to 80, so not linear

Consider if the model is quadratic, y equals k x squared

Use the first data point to find k

table row 20 equals cell k cross times 2 squared end cell row 20 equals cell 4 k end cell row k equals 5 end table

Use this to check the second data point

table row y equals cell 5 x squared end cell row y equals cell 5 open parentheses 4 close parentheses squared equals 80 end cell end table

It works for the second point, now check the third

y equals 5 open parentheses 6 close parentheses squared equals 180

Also correct for the third point, so this is an appropriate variation model

A quadratic variation model is suitable

Its full equation is bold italic y bold equals bold 5 bold italic x to the power of bold 2

If a cubic model is tested, y equals k x cubed, the first point produces the equation y equals 5 over 2 x cubed but this does not model the other two data points accurately

Worked Example

Two variation models are suggested for the data in the table below.

Model A: y equals 400 over x squared

Model B: y equals 800 over x cubed

x

5

6

10

15

y

25

15

3

2

Determine which variation model is more suitable.

Add a row to the table for each of the suggested models

Use the same given values of x (5, 6, 10, 15) to calculate the y values that each model predicts

E.g. To find the y value that model A predicts for x equals 5

y equals 400 over 5 squared equals 16

x

5

6

10

15

y

25

15

3

2

Model A: y equals 400 over x squared

16

11.111...

4

1.777...

Model B: y equals 800 over x cubed

6.4

3.703...

0.8

0.237...

Compare the modelled y values to the actual y values

The values for Model A are much closer to the actual values than Model B

Model A is more suitable

Last updated:

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Inverse ProportionNext:Exponential Growth & Decay
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.