Forming Equations from Shapes (Cambridge (CIE) IGCSE International Maths) : Revision Note
Forming Equations from Shapes
How do I form equations from shapes?
You need to use all the information given on the diagram and any specific properties of that shape
Common 2D shapes that you should know properties for are
Triangles: equilateral, isosceles, scalene, right-angled
Quadrilaterals: square, rectangle, kite, rhombus, parallelogram, trapezium
You may be asked about perimeter, area or angles
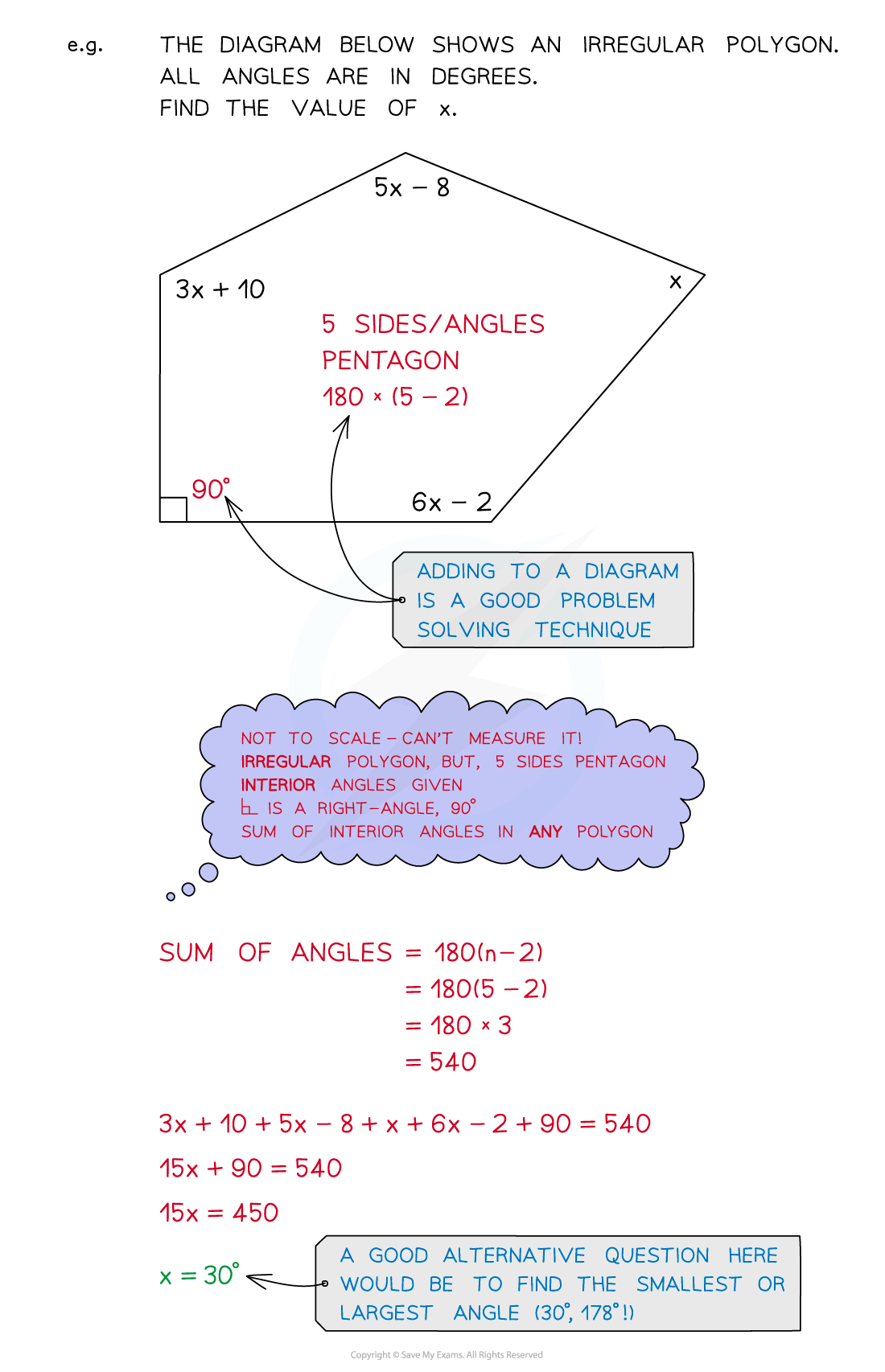
You may be asked about polygons
Regular vs irregular polygons
Interior vs exterior angles
The sum of interior angles is 180(n-2) for an n-sided polygon
You may be asked about angles in parallel lines
Alternative, corresponding and co-interior
You may be asked about 3D shapes involving surface area and volume
Prisms have constant cross sections
Volume is cross-section area multiplied by length
Is there anything else that can help?
Sketch a diagram if none is given
Split up uncommon shapes into the sum or difference of common shapes
Look out for important extra information
For example, a trapezium "with a line of symmetry"
With irregular shapes, assume all angles and lengths are different (unless told otherwise)
Put brackets around algebraic expressions when substituting them into geometric properties
Examiner Tips and Tricks
Read the question carefully - does it want an angle? perimeter? total area? curved surface area? etc.
For surface area and volume questions, check the list of formulas given in the exam.
Worked Example
A rectangle has a length of cm and a width of
cm.
Its perimeter is equal to 22 cm.
(a) Use the above information to find the value of x.
The perimeter of a rectangle is 2 × length + 2 × width
Expand the brackets
Simplify by collecting like terms
This perimeter is 22, so set this expression equal to 22
Solve this equation by adding 8 then dividing by 10
(b) Find the area of the rectangle.
The area of a rectangle is its length multiplied by is width
Substitute the value of x from part (a) into the length and width given in the question
length is 3 × 3 + 1 = 10
width is 2 × 3 - 5 = 1
Find the area (multiply length by width)
10 × 1
Include the correct units for area
Area = 10 cm2

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

