Speed (Cambridge (CIE) IGCSE International Maths)

Revision Note

Written by: Naomi C

Reviewed by: Dan Finlay

Did this video help you?

Speed

What is speed?

Speed is equal to distance divided by time

Speed is commonly measured in metres per second (m/s) or kilometres per hour (km/h)
- The units indicate speed is distance per time
  $Speed = \frac{Distance}{Time}$
'Speed' (in this formula) means 'average speed'
The formula can be rearranged to
- $Time = \frac{Distance}{Speed}$
- $Distance = Speed \times Time$
In harder problems there are often two journeys or two parts to one longer journey

What is a formula triangle?

A formula triangle shows the relationship between the different measures in a compound formula
They can be useful if you are less confident with rearranging formulas
For Speed, Distance and Time:

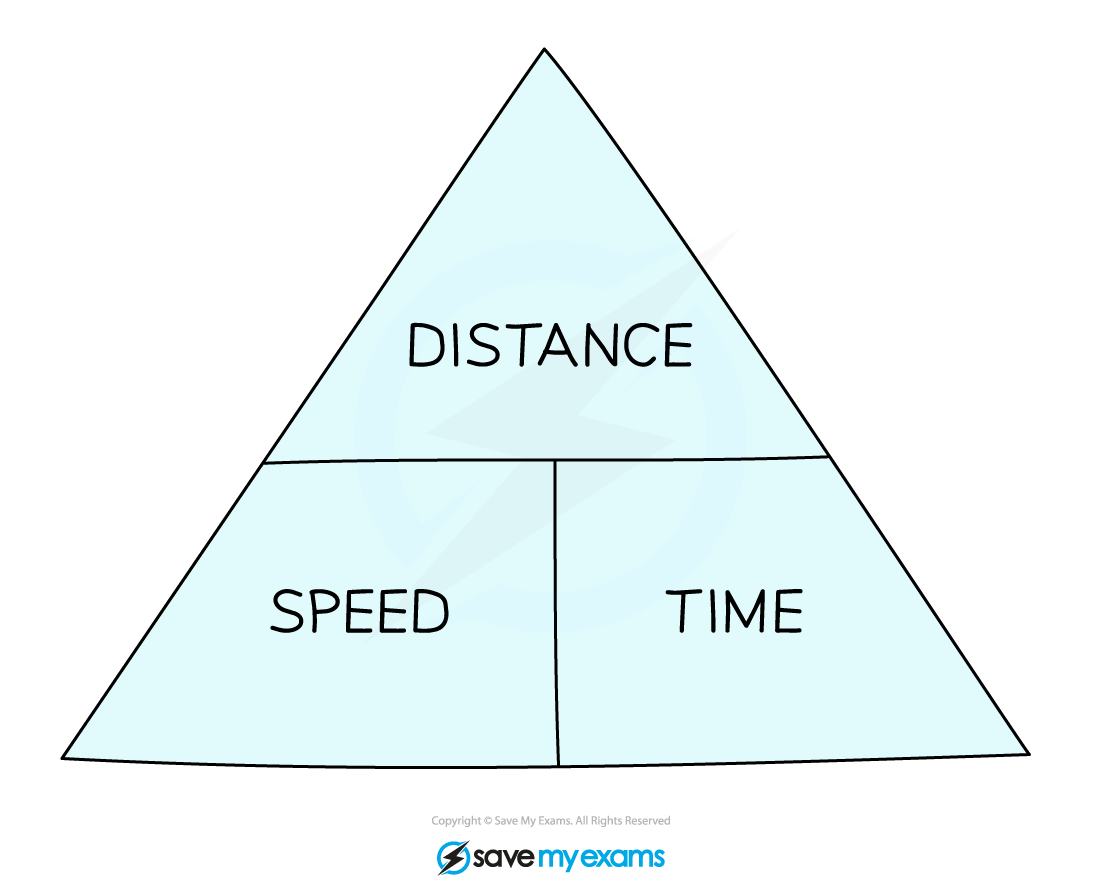
If you are calculating a variable on the top of the triangle, multiply the two variables on the bottom
- For example, $Distance = Speed \times Time$
If you are calculating a variable on the bottom of the triangle, divide the top by the other variable on the bottom
- For example, $Speed = Distance \div Time$ and $Time = Distance \div Speed$

Examiner Tips and Tricks

Look out for a mixture of units
- Time can be given as minutes but common phrases like 'half an hour' (30 minutes) could also be used in the same question
- Any mixed units should be those in common use and easy to convert, e.g. m to km etc

Worked Example

(a) A runner completes a 10 km race in three quarters of an hour.

Find the average speed of the runner in metres per second.
Round your answer to 3 significant figures.

As the answer must be in metres per second, convert the distance to metres, and the time to seconds

Multiply by 1000 to convert km to metres

10 km = 10 000 m

Write the time in minutes, you could calculate this as $\frac{3}{4} \times 60 mins$

Three quarters of an hour = 0.75 hrs = 45 mins

Multiply by 60 to convert minutes to seconds

45 × 60 = 2 700 seconds

Use the formula $Speed = \frac{Distance}{Time}$

$Speed = \frac{10000 m}{2700 s} = 3.703703 . . . m / s$

Round to 3 significant figures

3.70 m/s

(b) A sprinter's average speed when running 100 m is 8.85 m/s.

Calculate the total time taken in seconds for the sprinter to run 100 m.
Round your answer to the nearest hundredth of a second.

The units are already in metres, and metres per second, so do not need converting to reach an answer in seconds

Use the formula $Speed = \frac{Distance}{Time}$

$8.85 m / s = \frac{100 m}{Time}$

Rearrange to make the time the subject
Multiply both sides by time, and then divide both sides by the speed

$\begin{array}{rcl} 8.85 \times Time & = & 100 \\ Time & = & \frac{100}{8.85} \\ Time & = & 11.29943503 . . . \end{array}$

Round to the nearest hundredth of a second (2 decimal places)

11.30 s

Last updated: 18 October 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Squared & Cubic UnitsNext:Compound Measures