Revision NotesExam QuestionsFlashcardsPast Papers
IGCSEMathsCambridge (CIE)ExtendedRevision NotesVectors & TransformationsVectorsMagnitude of a Vector

Magnitude of a Vector (Cambridge (CIE) IGCSE Maths): Revision Note

Jamie Wood

Written by: Jamie Wood

Reviewed by: Dan Finlay

Updated on

Cambridge (CIE) Maths: ExtendedEdexcel Maths A (Modular): Higher Unit 2Edexcel Maths A: HigherCambridge (CIE) International Maths: Extended

Did this video help you?

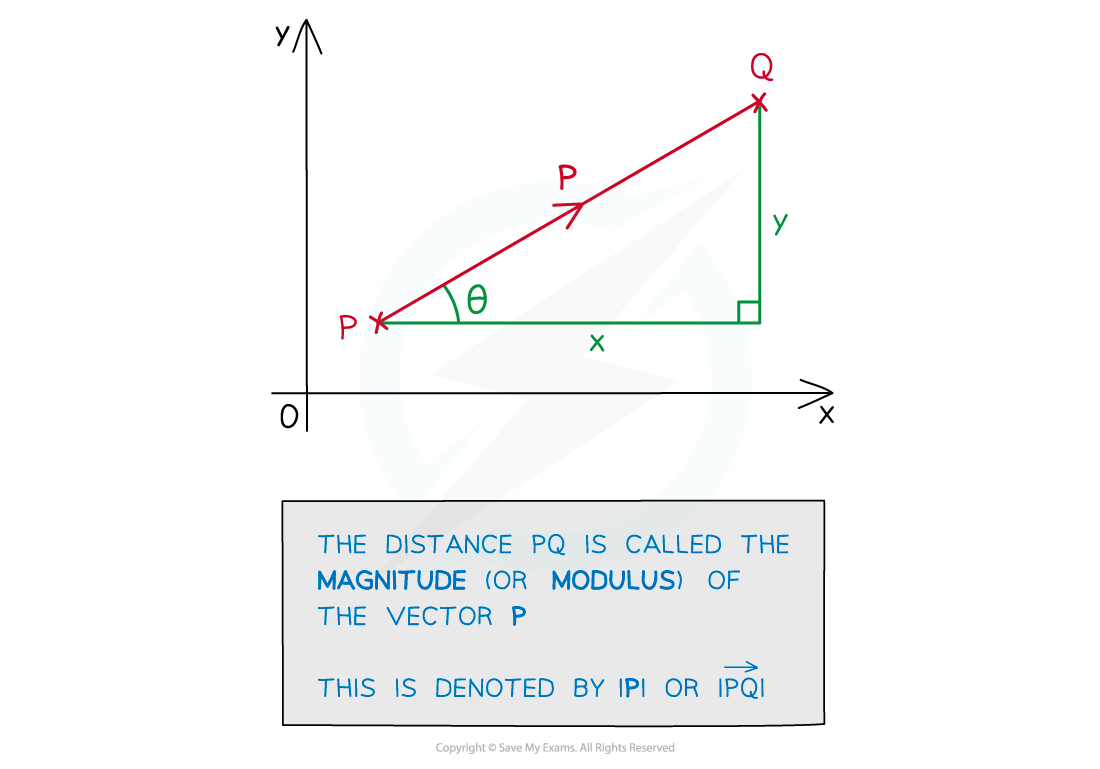
Magnitude of a Vector

How do I find the magnitude of a vector?

  • The magnitude of a vector is its length (distance)

    • It is also called the modulus

    • This is always a positive value

    • The direction of the vector is irrelevant

  • The magnitude of stack A B with italic rightwards arrow on top is written open vertical bar stack A B with rightwards arrow on top close vertical bar

    • The magnitude of a is written |a|

  • Depending on the use of the vector, the magnitude of a vector represents different quantities

    • For velocity, magnitude would be speed

    • For a force, magnitude would be the strength of the force (in Newtons)

  • In component form, the magnitude is the hypotenuse of a right-angled triangle

    • Use Pythagoras' theorem to find the magnitude

    • The magnitude of bold a equals blank open parentheses table row x row y end table close parentheses

      • open vertical bar bold a close vertical bar equals blank square root of x to the power of 2 space end exponent plus blank straight y squared end root

Diagram showing a vector P with horizontal component x and vertical component y. The magnitude of the vector is |P|.

Examiner Tips and Tricks

  • If there is no diagram, sketch one!

    • You can sketch a vector and use it to form a right-angled triangle

Worked Example

Consider two points A open parentheses negative 3 comma space 5 close parentheses and B open parentheses 7 comma space 1 close parentheses.

(a) Write down the column vector stack A B with rightwards arrow on top.

Find the horizontal and vertical distances between the two points
Subtract the x and y components of A from B

stack A B with rightwards arrow on top equals open parentheses table row cell 7 minus negative 3 end cell row cell 1 minus 5 end cell end table close parentheses

Error converting from MathML to accessible text.

(b) Find the modulus of vector stack A B with rightwards arrow on top.

Sketching a diagram of the vector stack A B with rightwards arrow on top can help

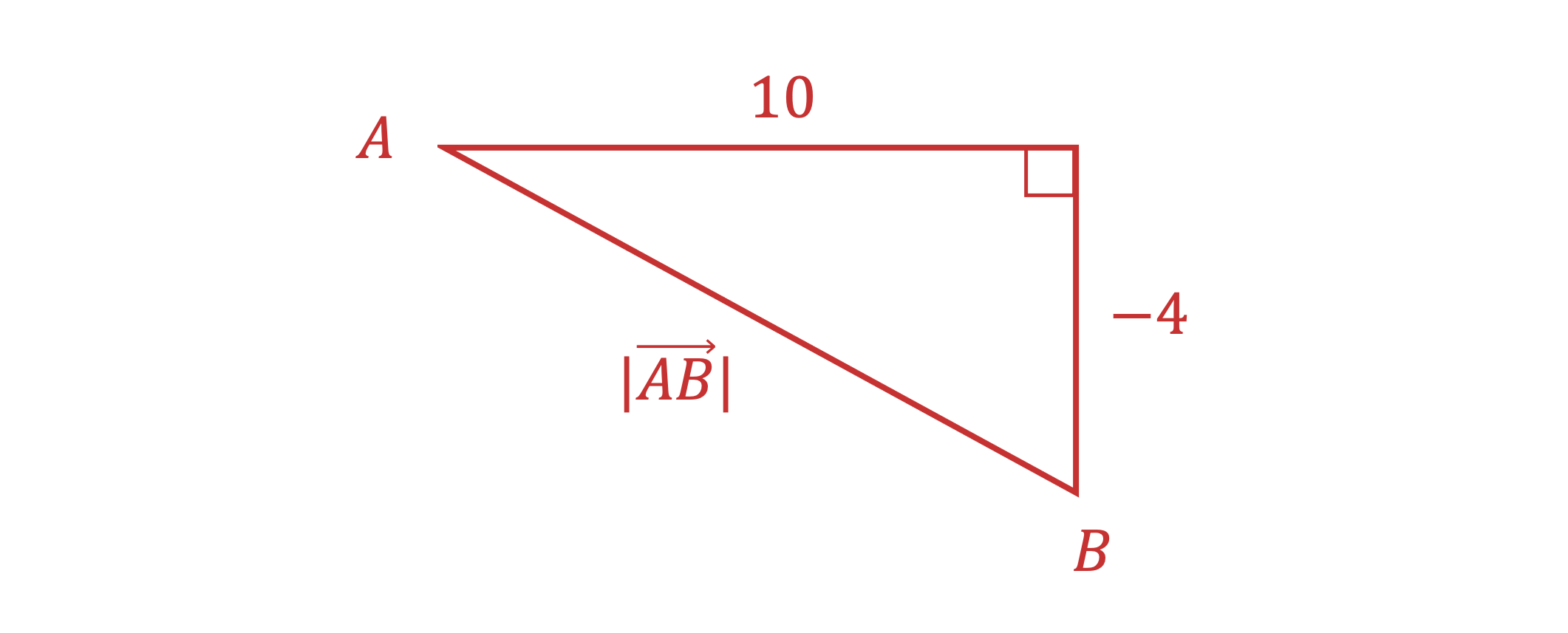
Right-angled triangle formed from points A and B. The horizontal distance is 10, the vertical distance is 4 and the hypotenuse is the magnitude of the vector from A to B.

Apply Pythagoras' theorem to the x and y components of stack A B with rightwards arrow on top

table row cell open vertical bar stack A B with rightwards arrow on top close vertical bar end cell equals cell square root of 10 squared plus open parentheses negative 4 close parentheses squared end root end cell row blank equals cell square root of 100 plus 16 end root end cell row blank equals cell square root of 116 end cell end table

Error converting from MathML to accessible text.

(c) Briefly explain why open vertical bar stack B A with rightwards arrow on top close vertical bar equals open vertical bar stack A B with rightwards arrow on top close vertical bar.

The magnitude of a vector is it's 'size'

Direction of the vector is ignored

open vertical bar stack B A with rightwards arrow on top close vertical bar equals open vertical bar stack A B with rightwards arrow on top close vertical bar since both vectors have the same distance

Another vector, stack C D with rightwards arrow on top, has three times the magnitude of vector stack A B with rightwards arrow on top.

(d) Write down a possible column vector for stack C D with rightwards arrow on top.

Being three times open vertical bar stack A B with rightwards arrow on top close vertical bar means the vector stack A B with rightwards arrow on top is three times longer

One way to find a vector is to multiply each component of the vector stack A B with rightwards arrow on top by 3 or -3

table row cell stack C D with rightwards arrow on top end cell equals cell 3 stack A B with rightwards arrow on top equals 3 open parentheses table row 10 row cell negative 4 end cell end table close parentheses end cell end table

Error converting from MathML to accessible text.

Another possible answer is Error converting from MathML to accessible text.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:Representing Vectors as DiagramsNext:Position & Displacement Vectors
    Author
    Reviewer
    Jamie Wood

    Author: Jamie Wood

    Expertise: Maths

    Jamie graduated in 2014 from the University of Bristol with a degree in Electronic and Communications Engineering. He has worked as a teacher for 8 years, in secondary schools and in further education; teaching GCSE and A Level. He is passionate about helping students fulfil their potential through easy-to-use resources and high-quality questions and solutions.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.