The Cosine Rule (Cambridge (CIE) IGCSE Maths)

Revision Note

Test yourself Flashcards

Written by: Naomi C

Reviewed by: Dan Finlay

Did this video help you?

Cosine Rule

What is the cosine rule?

The cosine rule is used in non right-angled triangles
- It allows us to find missing side lengths or angles
It states that for any triangle

$a^{2} = b^{2} + c^{2} - 2 b c \cos A$

Where
- $a$ is the side opposite angle A
- $b$ and $c$ are the other two sides
  - $b$ and $c$ are either side of angle A
  - A is the angle between them

Non Right-Angled Triangle labelled with angles A, B and C and opposite corresponding sides a, b and c.

How do I use the cosine rule to find a missing length?

Use the cosine rule for lengths
- when you have two sides and the angle between them
- and you want to find the opposite side, a
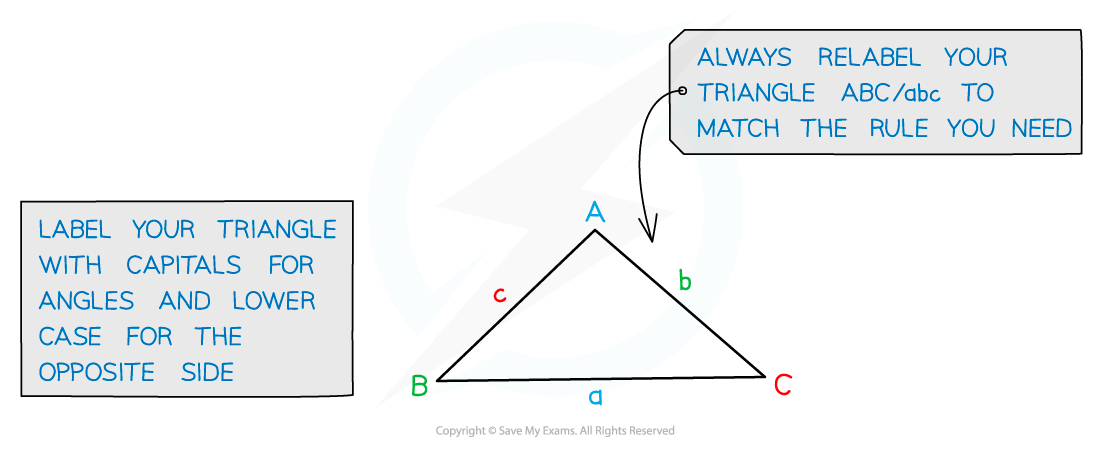
Start by labelling your triangle with the angles and sides
- Angles have upper case letters
- Sides opposite the angles have the equivalent lower case letter
Substitute values into $a^{2} = b^{2} + c^{2} - 2 b c \cos A$
- Make a the subject (don't forget to square root)

How do I use the cosine rule to find a missing angle?

Use the cosine rule for angles
- when you have all three sides
- and you want to find an angle
It helps to rearrange the formula as follows, by adding $2 b c \cos A$ to both sides then making $\cos A$ the subject

$\begin{array}{rcl} a^{2} & = & b^{2} + c^{2} - 2 b c \cos A \\ a^{2} + 2 b c \cos A & = & b^{2} + c^{2} \\ 2 b c \cos A & = & b^{2} + c^{2} - a^{2} \\ \cos A & = & \frac{b^{2} + c^{2} - a^{2}}{2 b c} \end{array}$

Use the formula $\begin{array}{rcl} \cos A & = & \frac{b^{2} + c^{2} - a^{2}}{2 b c} \end{array}$ to find the unknown angle A
- Remember, A is the angle between sides b and c
  - (you may need to relabel the triangle)
- You will need to use inverse cosine at the end, $\cos^{- 1} (. . .)$
Unlike the sine rule, there is no ambiguous case of the cosine rule

Examiner Tips and Tricks

You are given the cosine rule in the form $a^{2} = b^{2} + c^{2} - 2 b c \cos A$ on the formula sheet
Getting an error on your calculator when finding an angle may mean you have rearranged the formula incorrectly

Worked Example

The following diagram shows triangle $ABC$ , where $AB = 4.2 km$ , $BC = 3.8 km$ and $AC = 7.1 km$ .

Triangle ABC with AB = 4.2 km, BC = 3.8 km, AC = 7.1 km and angle ABC = θº.

Calculate the value of angle $ABC$ .

The side opposite the angle is 7.1, so $a = 7.1$

The sides 4.2 and 3.8 are $b$ and $c$ (in either order)

Use the cosine rule in the rearranged form $\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$

$\begin{array}{rcl} \cos θ & = & \frac{4 . 2^{2} + 3 . 8^{2} - 7 . 1^{2}}{2 (4.2) (3.8)} \\ θ & = & \cos^{- 1} (\frac{4 . 2^{2} + 3 . 8^{2} - 7 . 1^{2}}{2 (4.2) (3.8)}) \\ θ & = & 125.04699 . . . \end{array}$

$θ = 125.0 °$ (to 1 d.p.)

Last updated: 7 December 2024

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: