Conversion Graphs (Cambridge (CIE) IGCSE Maths) : Revision Note
Conversion Graphs
What is a conversion graph?
A conversion graph is a straight-line graph relating two quantities
You can convert (change) between them by reading values off the graph
Common examples include
Temperature
degrees Celsius (°C) and degrees Fahrenheit (°F)
Currency
Dollars ($) and Yen (¥)
Volume
Litres and gallons
Prices
A taxi driver charging per kilometre driven
The gradient of a conversion graph represents the rate of change
If the y-axis is the cost of a taxi journey (£) and the x-axis is the distance travelled (mile) then the gradient represents the cost per mile
A gradient of 5 means the cost increases by £5 for each mile travelled
How do I use a conversion graph?
Find the cost of 20kg using the conversion graph below
Start at 20kg on the x-axis
Draw a vertical line to the graph
Then a horizontal line across to the y-axis
Read off the value
$12
Find how many kilograms can be bought with $30
Start at $30 on the y-axis
Draw a horizontal line to the graph
Then a vertical line down to the x-axis
Read off the value
50kg
You can use proportion to find values that on not on the axes
To find the cost of 120kg
120kg = 6 × 20kg costs 6 × $12 = $72
120kg = 50kg + 50kg + 20kg costs $30 + $30 + $12 = $72
You can only do this if the graph starts at the origin
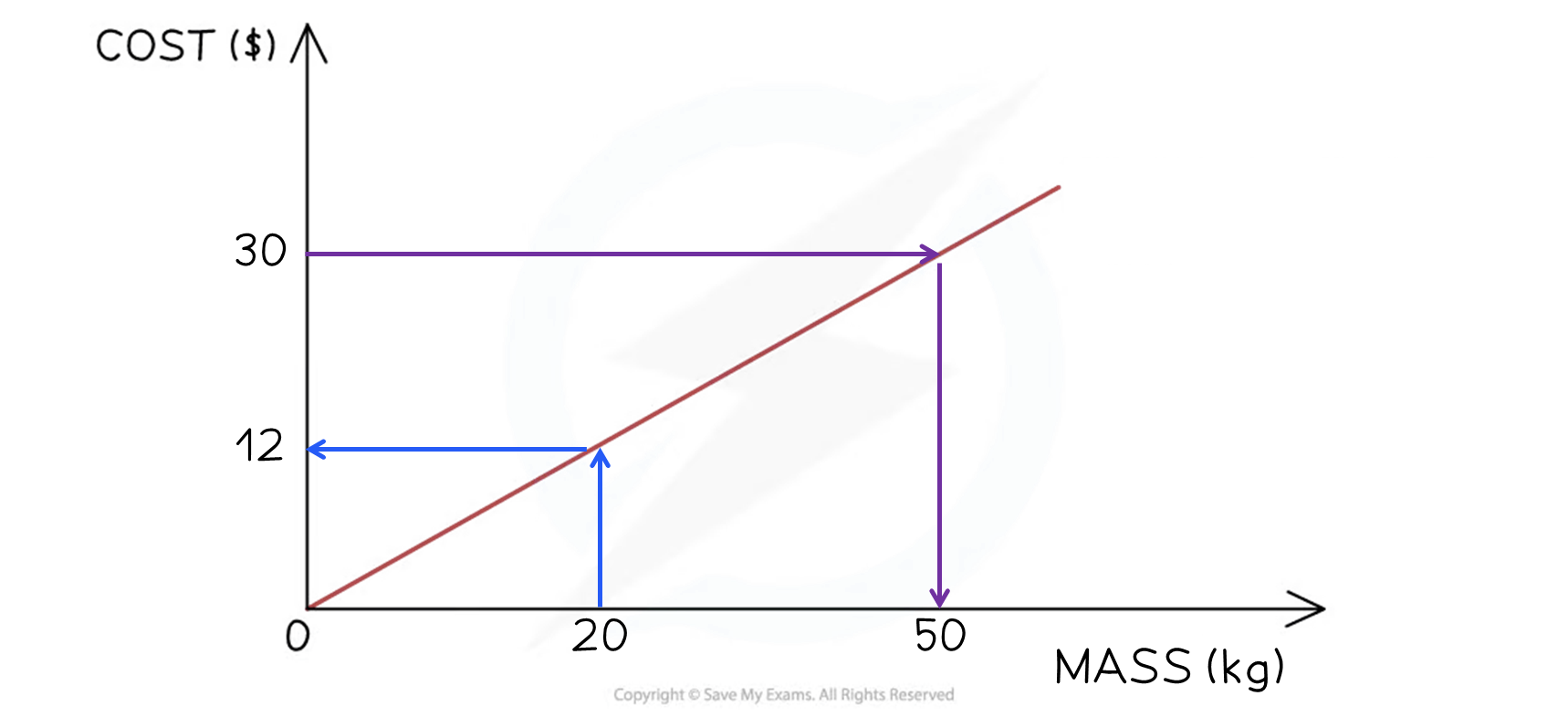
How do I use a conversion graph that does not start at the origin?
Convert 100°F into Celsius using the conversion graph below
Start at 100°F on the y-axis
Draw a horizontal line to the graph
Then a vertical line down to the x-axis
Read off the value
37.5°C
Answers between 37°C and 38°C would be accepted
(The true answer is 37.8°C to 1 decimal place)
The graph starts at 32 on the y-axis
This means that 0°C is 32°F
This starting value sometimes represents a fixed cost when money is involved
It could represent the fixed charge for the cost of a taxi fare
To convert values that are not on the axis
You would need to find an equation for the straight-line

Examiner Tips and Tricks
Always check the scales of the axes!
Worked Example
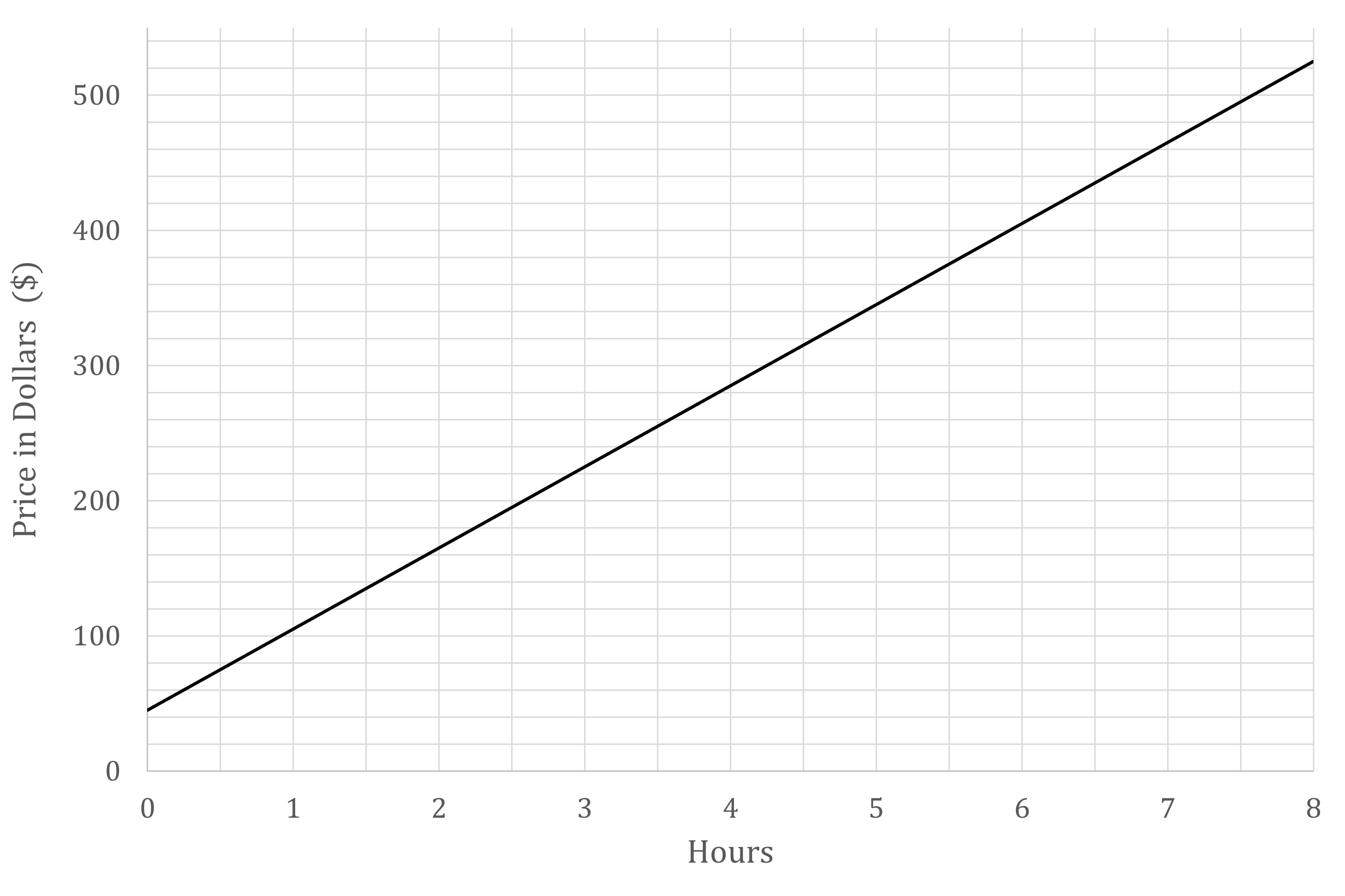
The graph below shows the price (in dollars, $) charged by a plumber for the time spent (in hours) on a particular job.
(a) Estimate the price charged for a job that takes 3 hours.
Draw a vertical line up from the x-axis at 3 hours
Then a horizontal line across to the y-axis
Read off the value
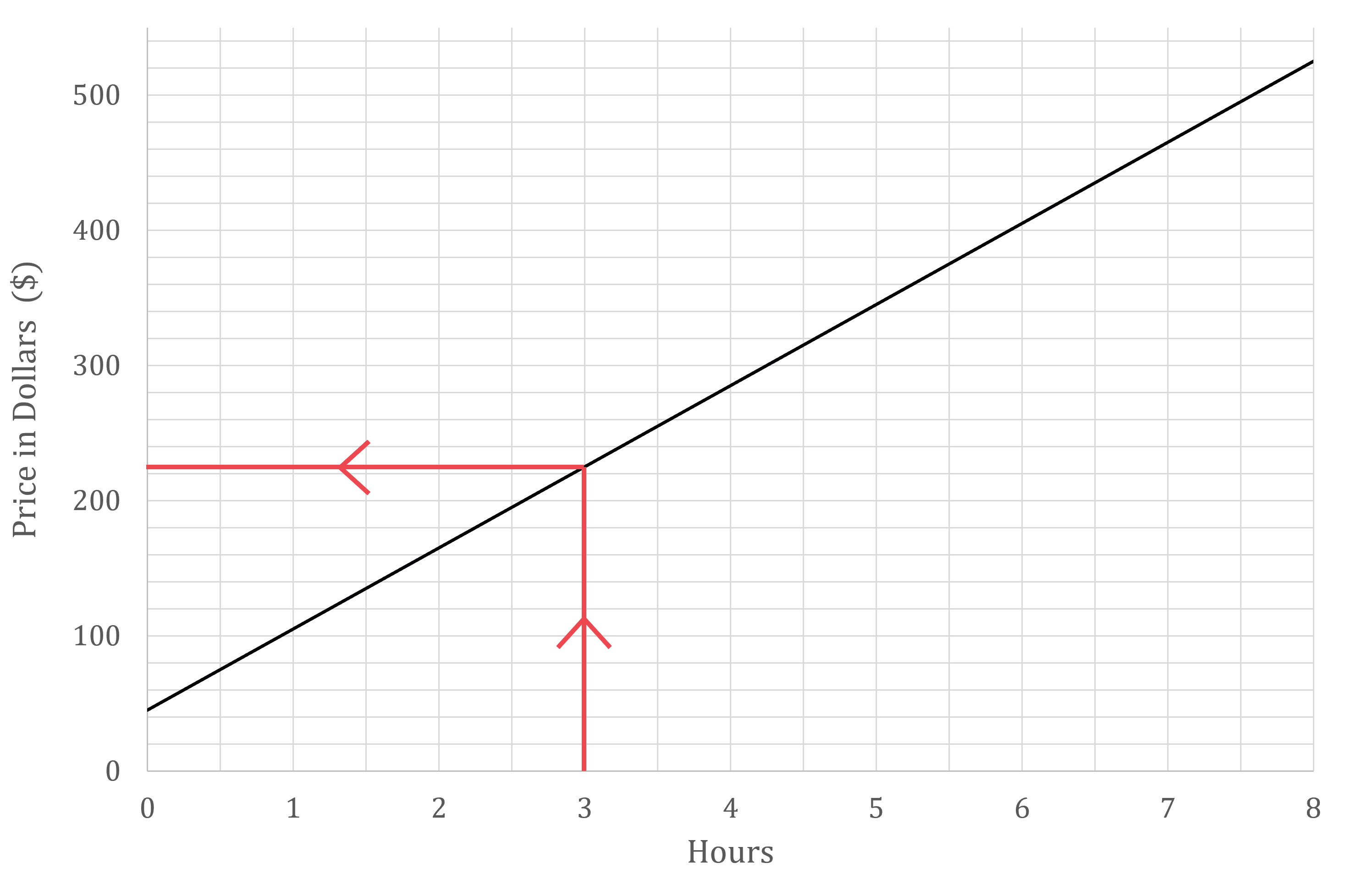
Approximately $225
Answers between $220 and £230 are accepted
(b) A particular job costs $320. Estimate, to the nearest half hour, how long this job took.
Draw a horizontal line across from the y-axis at $320
Draw a vertical line down to the x-axis
Read off the value to the nearest 0.5 hours
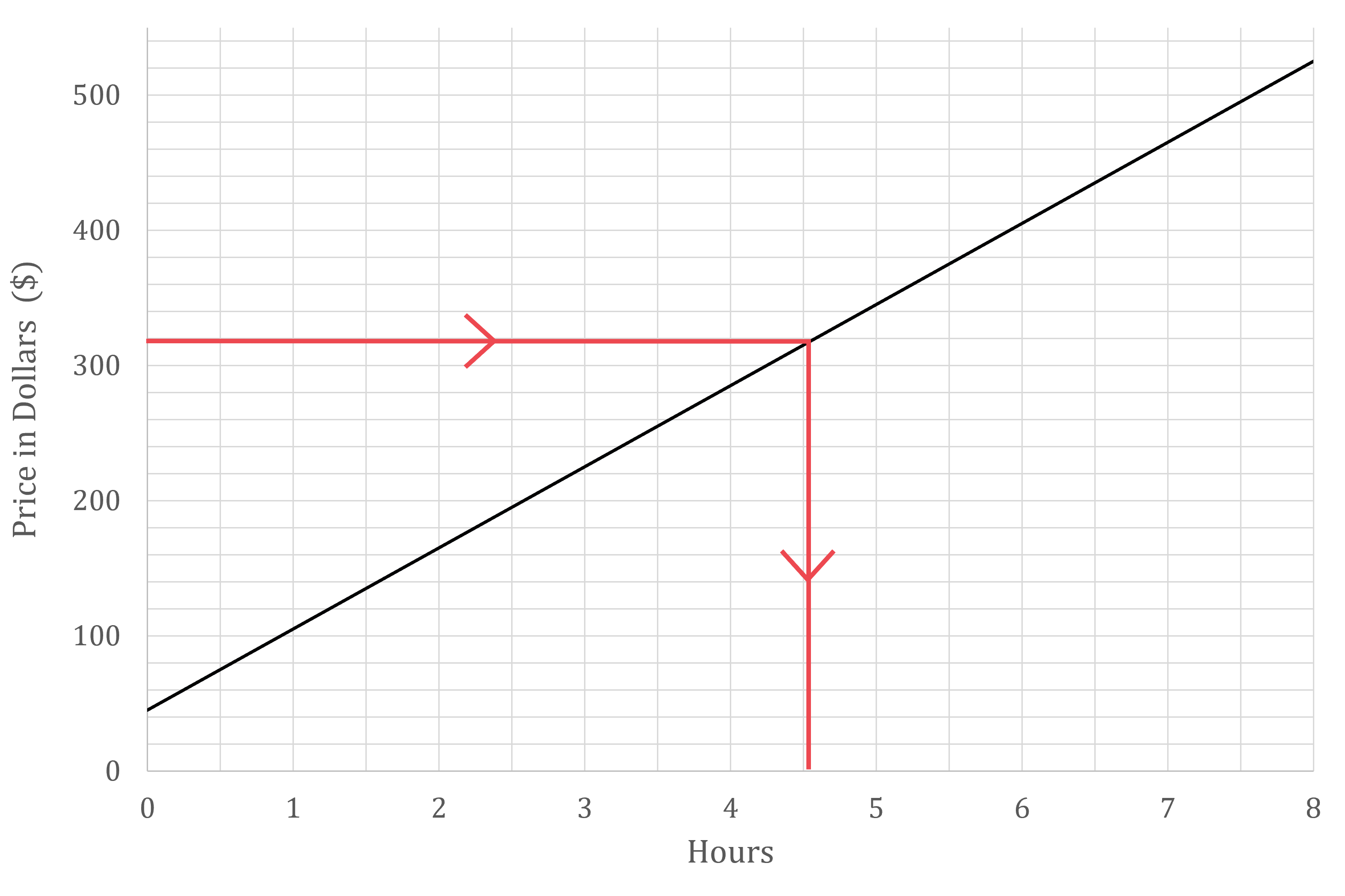
4.5 hours (to the nearest half hour)
(c) The plumber charges a fixed callout fee for travelling to the customer and inspecting the job before starting any work.
Find the price of the callout fee.
Before starting work means 0 hours of work has been done
Find the price charged for 0 hours
This is the y-intercept of the graph
Approximately $45
Answers between $40 and £50 are accepted

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

