Problem Solving with Differentiation (Cambridge (CIE) IGCSE Maths)

Revision Note

Test yourself Flashcards

Written by: Mark Curtis

Reviewed by: Dan Finlay

Did this video help you?

Problem Solving with Differentiation

What is problem solving using differentiation?

You can use the same method of differentiating curves to find turning points to help with problems involving finding the maximum or minimum value of a quantity
- These are called optimisation problems
Questions may use different variables
- For example, $A = t^{3} - 12 t$ and $\frac{d A}{d t} = 0$

How do I apply differentiation to different contexts?

This is easiest explained using an example

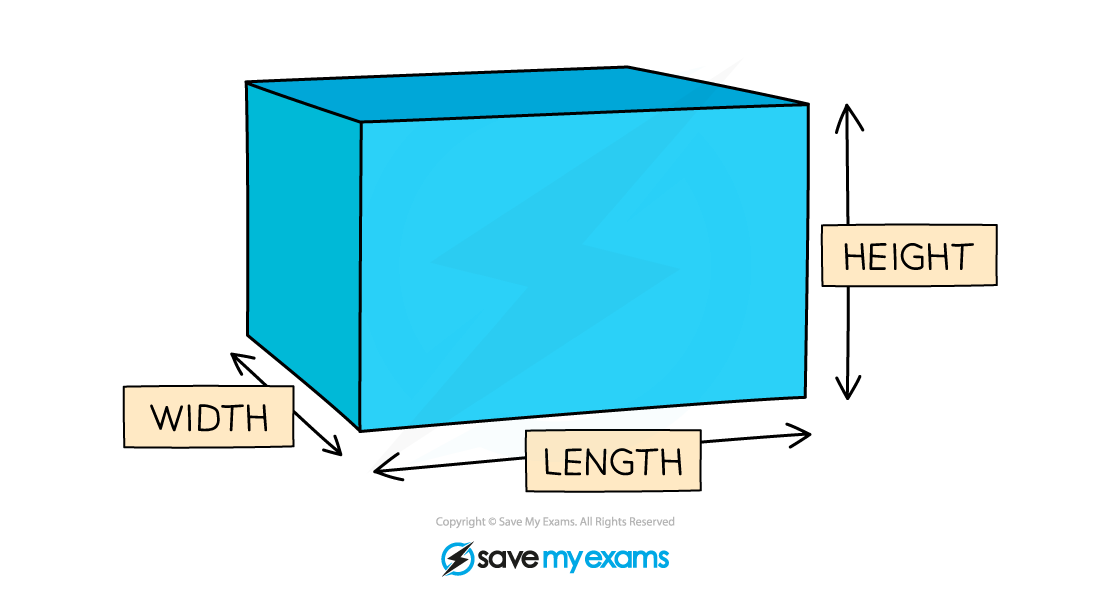
Diagram of a cuboid with the width, length and height labelled.

Find the maximum volume, $V$ m³, of the cuboid shown with width 2 m, length $x$ m and height $(10 - x)$ m
- Find a formula for its volume in terms of $x$
- Volume = width $\times$ length $\times$ height
  - $V = 2 x (10 - x)$
- Expand this into individual terms in $x$
  - $V = 20 x - 2 x^{2}$
  - This is a negative quadratic in $x$ (it has an $\cap$ shape)
The graph of $V$ against $x$ will have a maximum point when $\frac{d V}{d x} = 0$
- Find $\frac{d V}{d x}$ by differentiating each term
  - $\frac{d V}{d x} = 20 - 4 x$
- Set this equal to zero and solve
  - $\begin{array}{rcl} 20 - 4 x & = & 0 \end{array}$ so $4 x = 20$ giving $x = 5$
  - This is the value of $x$ at the maximum point (not the value of $V$ )
- Substitute this value of $x$ back into the equation for $V$
  - $V = 20 \times 5 - 2 \times 5^{2} = 50$
  - The maximum volume is 50 m³

Examiner Tips and Tricks

A common problem in the exam is to forget to substitute the value of $x$ back into the formula!

How do I know if I have found a maximum value or a minimum value?

Sometimes there are two values of $x$ for different turning points and you need one of them
- either substitute them both back into the formula
  - See which gives the max value and which gives the min value
- or use any acceptable techniques for classifying turning points
  - For example, using a sketch to see if its a max or min
- Remember that
  - Positive quadratics have minimum points
  - Negative quadratics have maximum points

How do I use differentiation if there are lots of variables?

Sometimes a formula has lots of letters
- You need to find an extra relationship between these letters
- then substitute it into the formula
If, in the above example, you had width 2 m, length $x$ m and height $y$ m then
- $V = 2 x y$
  - But you need a formula in $x$ only
- You will be given an extra piece of information, such as the length and height sum to 10 m
  - Therefore $x + y = 10$
  - Make $y$ the subject, $y = 10 - x$
  - Substitute it into $V$ to get $V = 2 x (10 - x)$

Worked Example

A farmer has 60 metres of fencing and wants to fence off the biggest rectangular area possible next to an existing wall.

The area has dimensions $x$ metres by $y$ metres, as shown.

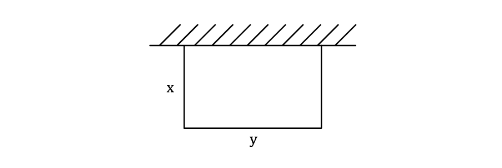
Image of the farmer's fence attached to a wall. There are three sides of fencing forming a rectangular area with the wall. The width of the rectangle is x and the length is y.

(a) Explain why $2 x + y = 60$ .

The wall is not part of the fencing

Find the total length of the three sides of the fence shown

$x + y + x$

This must equal 60 metres

The length of the fence must equal 60 metres so $2 x + y = 60$

(b) Show that the area, $A$ m², is given by $A = 60 x - 2 x^{2}$ .

Find the area of the rectangle shown

$A = x y$

You need a right-hand side in terms of $x$ only

Make $y$ the subject of part (a)

$y = 60 - 2 x$

Substitute this into the area formula

$A = x (60 - 2 x)$

This is now all in terms of $x$

Expand

$A = 60 x - 2 x^{2}$

To find a maximum point, set $\frac{d A}{d x} = 0$

First find $\frac{d A}{d x}$ by differentiating each term

$\frac{d A}{d x} = 60 - 4 x$

Set this equal to zero and solve

$\begin{array}{rcl} 60 - 4 x & = & 0 \\ 4 x & = & 60 \\ x & = & \frac{60}{4} \\ x & = & 15 \end{array}$

This is the value of $x$ at the maximum point (but not the maximum of $A$ )

Substitute this value of $x$ back into $A$

$\begin{array}{rcl} A & = & 60 \times 15 - 2 \times 15^{2} \\ = & 450 \end{array}$

The maximum area is 450 m²

(d) Explain how you know that the answer in part (c) is a maximum area, not a minimum area.

See how the area $A$ depends on $x$

Think about what it would look like as a graph

$A = 60 x - 2 x^{2}$ is a negative quadratic curve

A negative quadratic curve has an $\cap$ shape

There is only one turning point on this graph and it is a maximum point

The curve $A = 60 x - 2 x^{2}$ is a negative quadratic curve

This means it can only have a maximum point, not a minimum point

Last updated: 17 October 2024

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: