Finding Stationary Points & Turning Points (Cambridge (CIE) IGCSE Maths) : Revision Note
Did this video help you?
Finding Stationary Points & Turning Points
What is a stationary point?
A stationary point is a point on the graph at which the gradient is zero (a tangent drawn at this point will be horizontal)
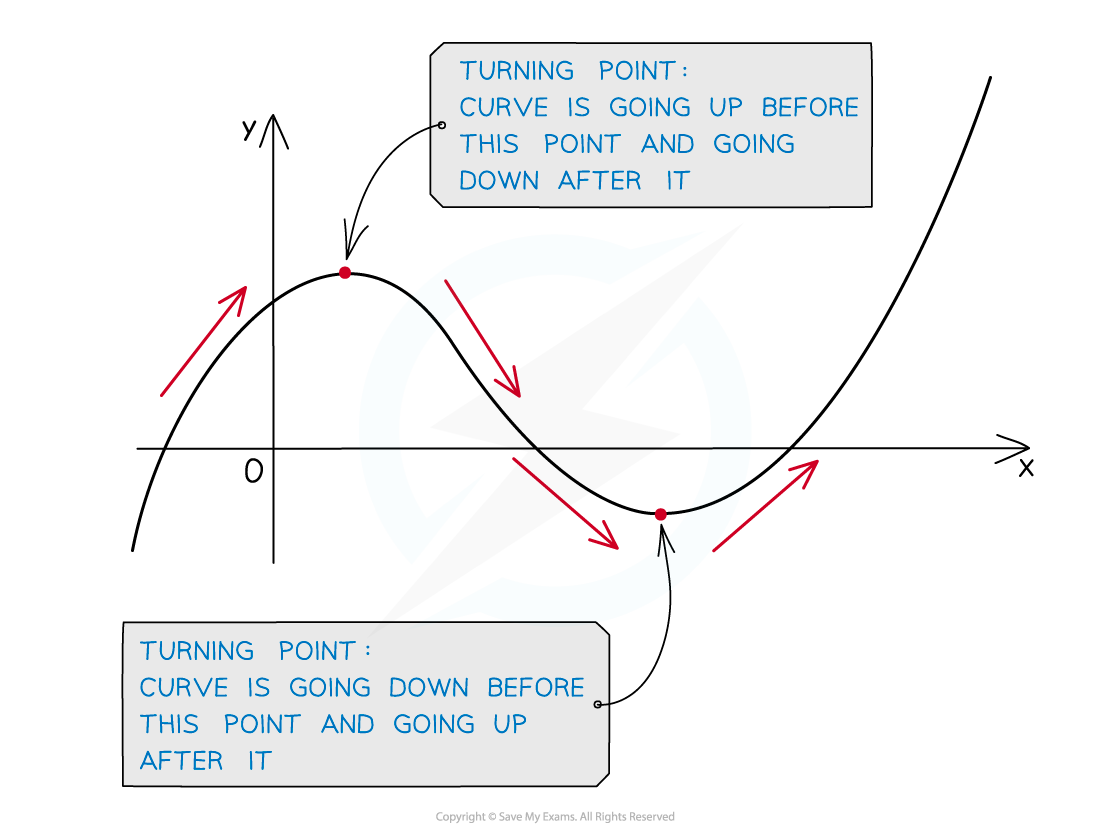
These include peaks (maximum points) and troughs (minimum points)
Maximum points and minimum points are collectively know as turning points
At a turning point a curve changes from moving upwards to moving downwards, or vice versa
At a turning point the gradient of the curve is zero
If a tangent is drawn at a turning point it will be a horizontal line
Horizontal lines have a gradient of zero
Because the gradient at a turning point is zero
Substituting the x-coordinate of a turning point into the gradient function
(the derivative) will give an output of zero

How do I find the coordinates of a turning point?
STEP 1
Find the gradient function (derivative)of the original equation
E.g. Find the coordinates of the turning point of the equation
STEP 2
Set the gradient function (derivative) equal to zero and solve forThis will find the x-coordinate of the turning point
E.g.
, so
STEP 3
Substitute the x-coordinate into the original equation of the graphThis will find the y-coordinate of the turning point
E.g.
STEP 4
Write out the coordinates of the turning point
E.g. The turning point is at
Examiner Tips and Tricks
Remember to read the questions carefully
Sometimes only the x-coordinate of a turning point is required
Worked Example
Find the coordinates of the turning point on the curve with equation .
Use differentiation to find the gradient function (derivative) of the equation
Set the derivative equal to 0 and solve for x
Substitute the x-coordinate into the origination equation of the curve and solve for y
Form a set of coordinates
The turning point has coordinates

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

