Sin, Cos & Tan (Edexcel IGCSE Further Pure Maths): Revision Note
Exam code: 4PM1
Defining Sin, Cos and Tan
What is the unit circle?
The unit circle is a circle with radius 1 and centre (0, 0)
It helps us to define values for sin θ, cos θ and tan θ for all values of θ
or
doesn't make sense as an angle in a triangle or other shape
But sin θ, cos θ and tan θ are defined for 'angles' like that
On the unit circle
Angles are always measured from the positive x-axis and turn:
anticlockwise for positive angles
clockwise for negative angles
After
you can keep going
So
is 'all the way around' anticlockwise (
) and then another
anticlockwise
Or
is 'all the way around twice' clockwise (
) and then another
clockwise
It can be used to calculate trig values as coordinates (x, y) on the circle
Make a right triangle with the radius as the hypotenuse
θ is the angle measured anticlockwise from the positive x-axis
(or clockwise for negative θ)
The x-axis will always be adjacent to the angle, θ
SOHCAHTOA can then be used to find the values of sinθ, cosθ and tanθ
As the radius is 1 unit
the x coordinate gives the value of cos θ
the y coordinate gives the value of sin θ
Dividing the y coordinate by the x coordinate gives the value of tan θ
This is also the gradient of the line through the origin and the point on the unit circle
Unlike SOHCAHTOA this allows us to calculate sin, cos and tan for
angles greater than 90° (
radians)
negative angles
Worked Example
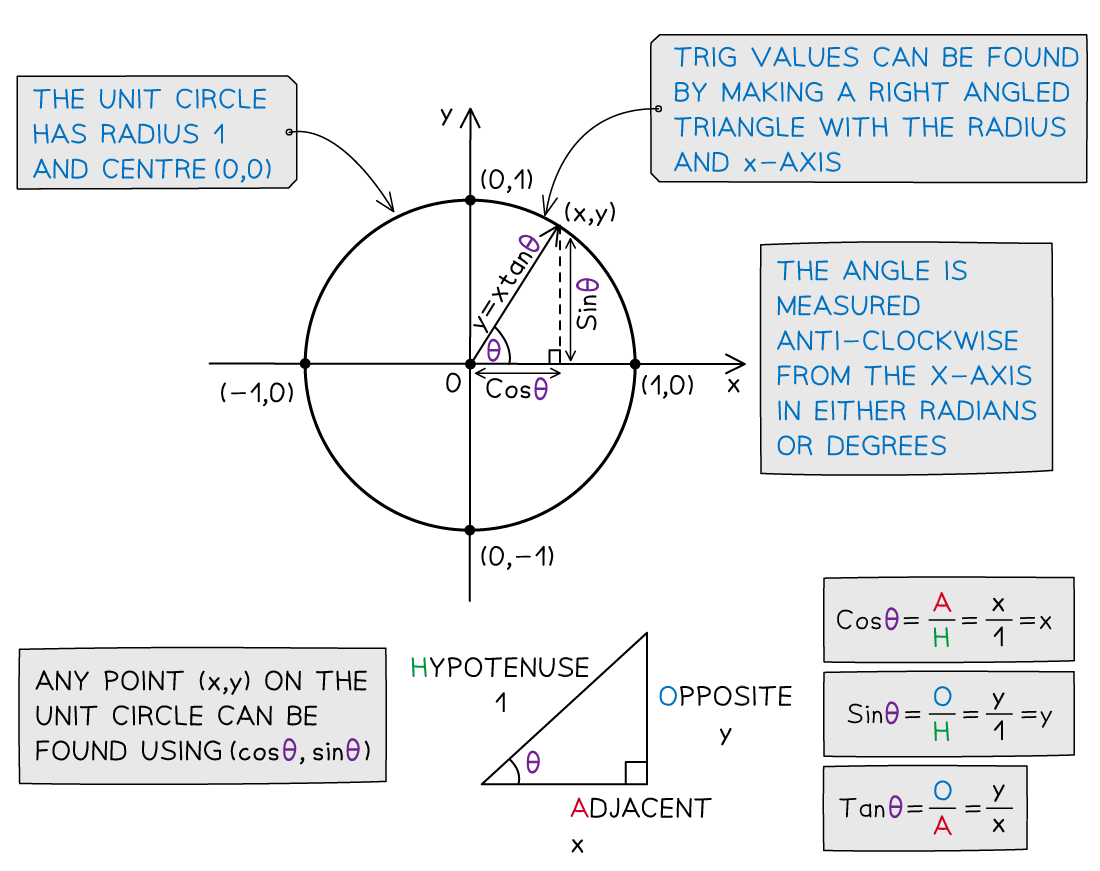
The coordinates of a point on a unit circle, correct to 3 significant figures, are (0.629, 0.777). Find the angle with the positive x-axis, θ°, to the nearest degree.
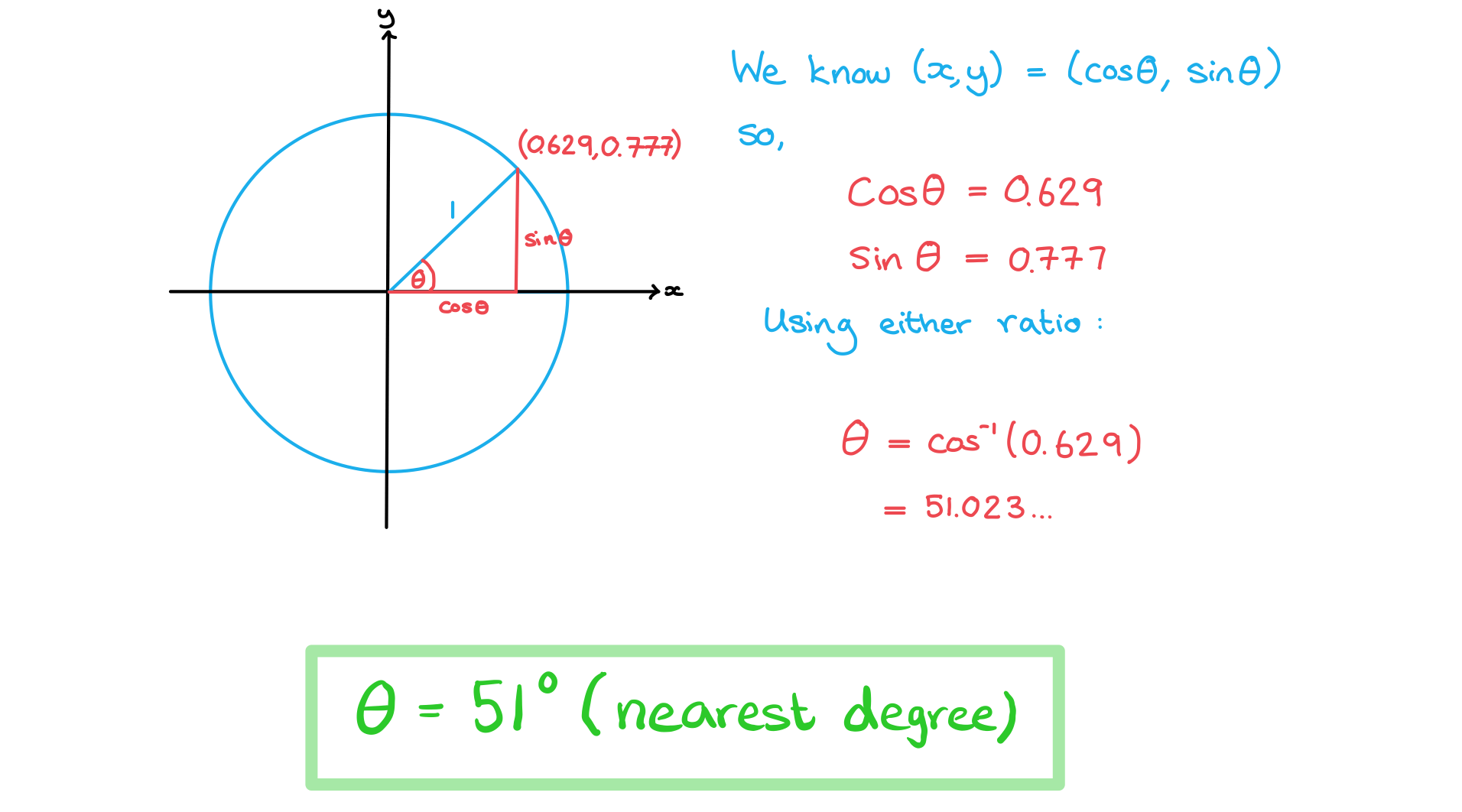
Using The Unit Circle
What are the properties of the unit circle?
The unit circle can be split into four quadrants
The first quadrant is for angles between 0 and 90°
All three of sin θ, cos θ and tan θ are positive in this quadrant
The second quadrant is for angles between 90° and 180° (
rad and
rad)
Sine (sin θ ) is positive in this quadrant
The third quadrant is for angles between 180° and 270° (
rad and
rad)
Tangent (tan θ ) is positive in this quadrant
The fourth quadrant is for angles between 270° and 360° (
rad and
rad)
Cosine (cos θ ) is positive in this quadrant
Starting from the fourth quadrant (on the bottom right) and working anti-clockwise
the positive trig functions spell out CAST
This is why it is often thought of as the CAST diagram
You may have your own way of remembering this
A popular one starting from the first quadrant is All Students Take Calculus
To help yourself picture this try sketching all three trig graphs on one set of axes
Look at which graphs are positive in each 90° section
How is the unit circle used to find additional solutions?
Trigonometric functions have more than one 'input' for each 'output'
For example sin 30° = sin 150° = 0.5
This means that trigonometric equations have more than one solution
Both 30° and 150° satisfy the equation
The unit circle can be used to find all solutions to trigonometric equations in a given interval
Your calculator will only give one solution to an equation like
This solution is called the primary value
However due to the periodic nature of the trig functions there there are an infinite number of solutions
You need to be able to find such additional values
On the exam you will be given an interval in which the solutions should be found
This could either be in degrees or in radians
If you see π or some multiple of π then you must work in radians
The following steps can help you use the unit circle to find additional values
STEP 1
Draw the primary value angle using the x or y coordinates to help youThis will be in the first or second quadrants if using
to get the primary angle
Or in the first or fourth quadrants if using
or
If you are working with
draw the line from the origin to the circumference of the circle
the point on the circumference is where the y coordinate is k
If you are working with
draw the line from the origin to the circumference of the circle
the point on the circumference where the x coordinate is k
If you are working with
draw the line from the origin to the circumference of the circle
such that the gradient of the line is k
This will give you the angle which should be measured from the positive x-axis…
… anticlockwise for a positive angle
… clockwise for a negative angle
STEP 2
Draw the radius in the other quadrant which has the same...... x coordinate if solving
This will be the quadrant which is vertically below the original quadrant
... y coordinate if solving
This will be the quadrant which is horizontally to the left of the original quadrant
... gradient if solving
This will be the quadrant which is diagonally opposite to the original quadrant
STEP 3
Work out the size of the second angle, measuring from the positive x-axis… anticlockwise for a positive angle
or clockwise for a negative angle
Look at the given interval of solution values
This will help you to decide whether you need a negative or positive angle measure
STEP 4
Add or subtract (multiples of) either 360° or 2π radians to or from both valuesuntil you have all solutions in the required interval
Examiner Tips and Tricks
Practice sketching out the unit circle
and using CAST to remember what is positive in what quadrant
This can help you to find all solutions to a problem in an exam question
Worked Example
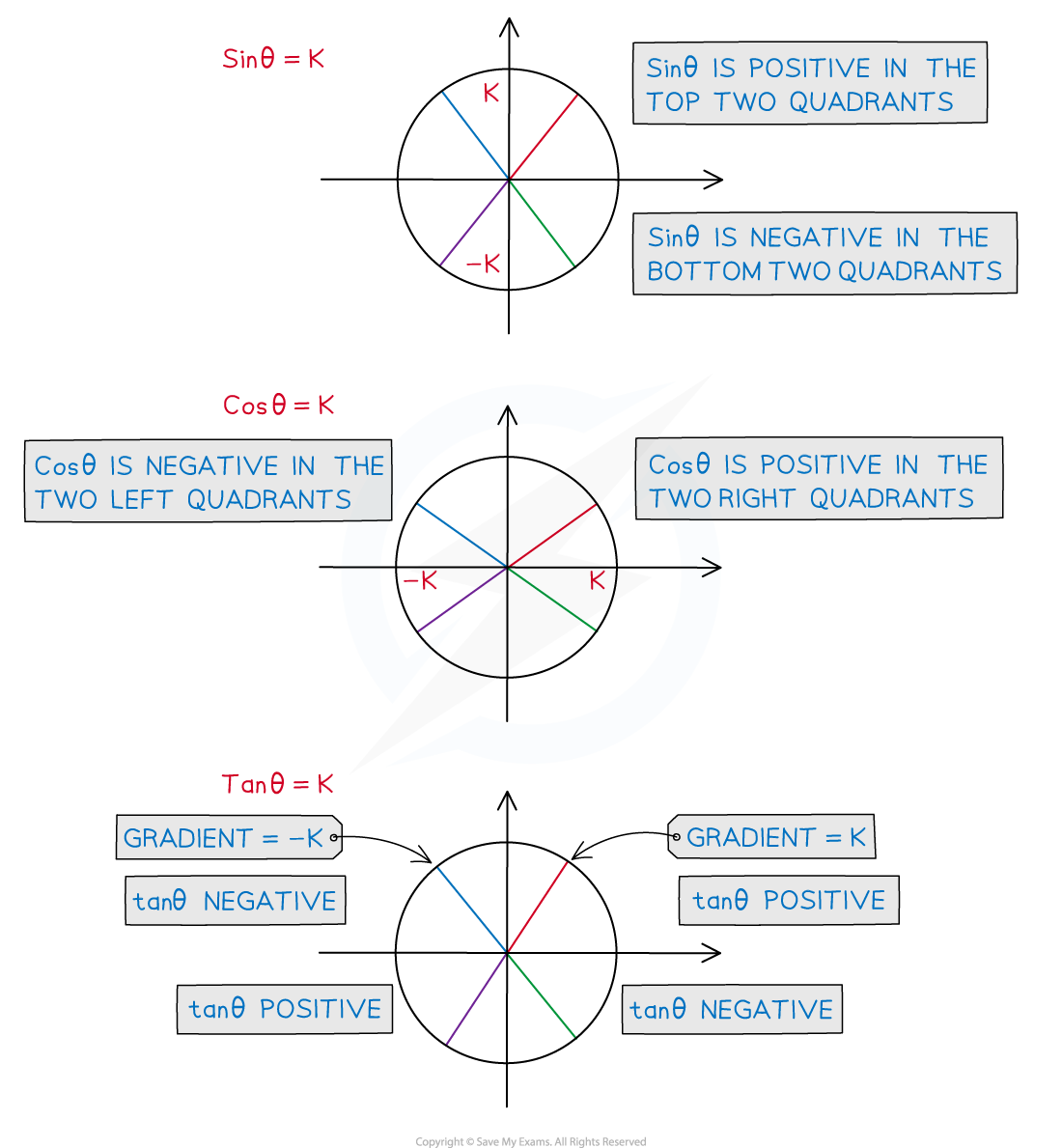
It is given that one solution of is θ = 0.6435 radians, correct to 4 decimal places.
Use this to find all other solutions in the interval , giving your answers correct to 3 significant figures.
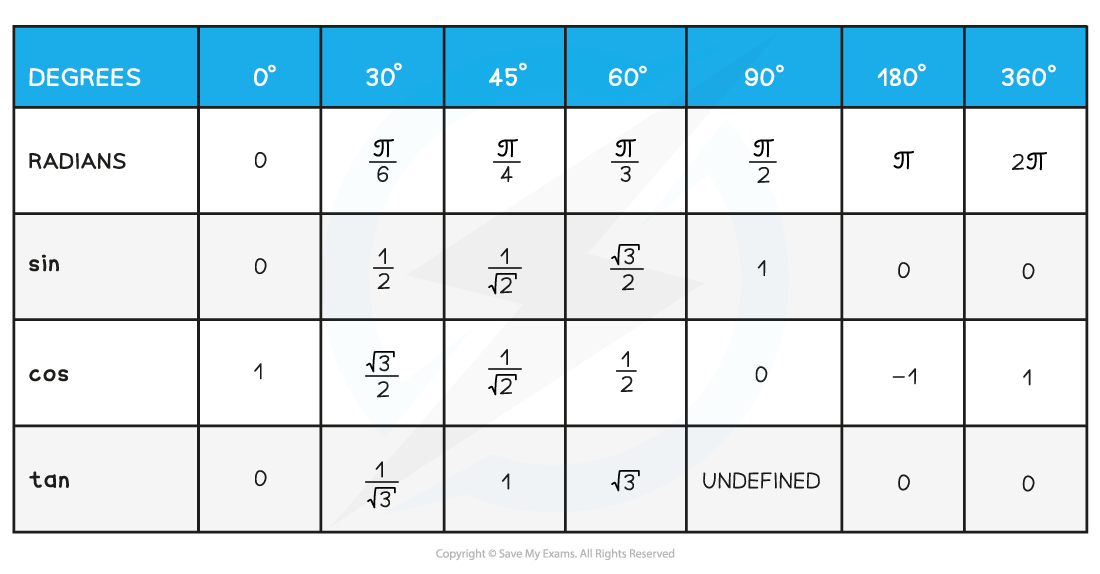
Trigonometry Exact Values
What are exact values in trigonometry?
For certain angles the values of sin θ, cos θ and tan θ can be written exactly
This means using fractions and surds
You should be familiar with these values
and able to derive them using geometry
You should know the exact values of sin, cos and tan for angles of
0°, 30°, 45°, 60°, 90°, and 180° (in degrees)
or
and
(in radians)
These values are in the following table
Note that for 360° (
radians) the trig values are all the same as for 0
How do I find the exact values of other angles?
The exact values for cos and sin can be seen on the unit circle
They are the x and y coordinates respectively
If using the unit circle coordinates to memorise the exact values
remember that cos (x value) comes before sin (y value)
The unit circle can also be used to find exact values of other angles using symmetry
If you know the exact values for an angle in the first quadrant
you can draw the same angle from the x-axis in other quadrants to find values for other angles
Remember that the angles are measured anticlockwise from the positive x-axis
For example if you know that the exact value for sin 30° is 0.5
draw a 30° angle from the horizontal axis in the three other quadrants
measuring from the positive x-axis you have the angles of 150°, 210° and 330°
sine is positive in the second quadrant so sin 150° = 0.5
sine is negative in the third quadrant so sin 210° = - 0.5
sine is negative in the fourth quadrant so sin 330° = - 0.5
It is also possible to find the negative angles by measuring clockwise from the positive x-axis
draw a 30° angle from the horizontal in the three other quadrants
measuring clockwise from the positive x-axis you have the angles of -30°, -150°, -210° and -330°
sin is negative in the fourth quadrant so sin(-30°) = - 0.5
sin is negative in the third quadrant so sin(-150°) = - 0.5
sin is positive in the second quadrant so sin(-210°) = 0.5
sin is positive in the fourth quadrant so sin(-330°) = 0.5

How can I derive exact trig values?
Being able to derive basic exact trig values can help if you forget them
Values for 30° and 60° (
and
radians) can be derived by using an equilateral triangle
See the Worked Example below
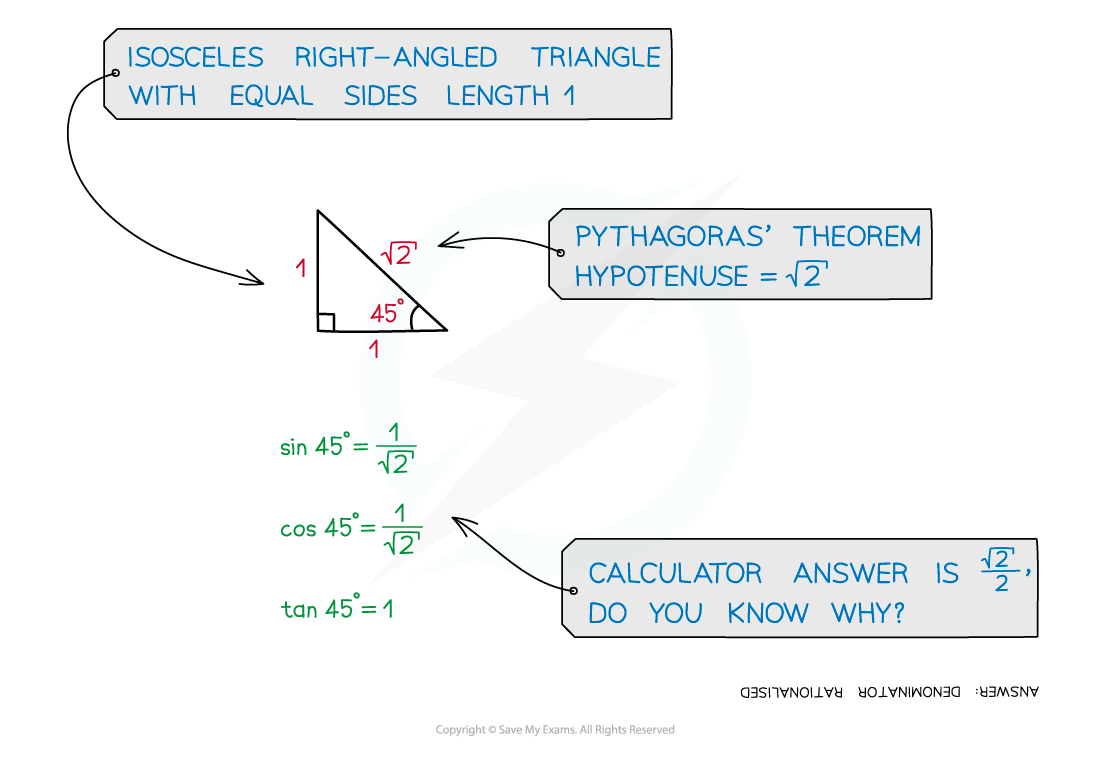
Values for 45° (
radians) can be derived using a right-angled isosceles triangle
See the following diagram
Examiner Tips and Tricks
It can be easy to muddle up exact trig values if you just try to remember them from a list,
Sketch the unit circle and/or trig graphs on your exam paper
This can help you keep the trig functions and their values straight
Note that for
,
,
,
,
The sine values run
The cosine values run
Values for tangent can be found using
Worked Example
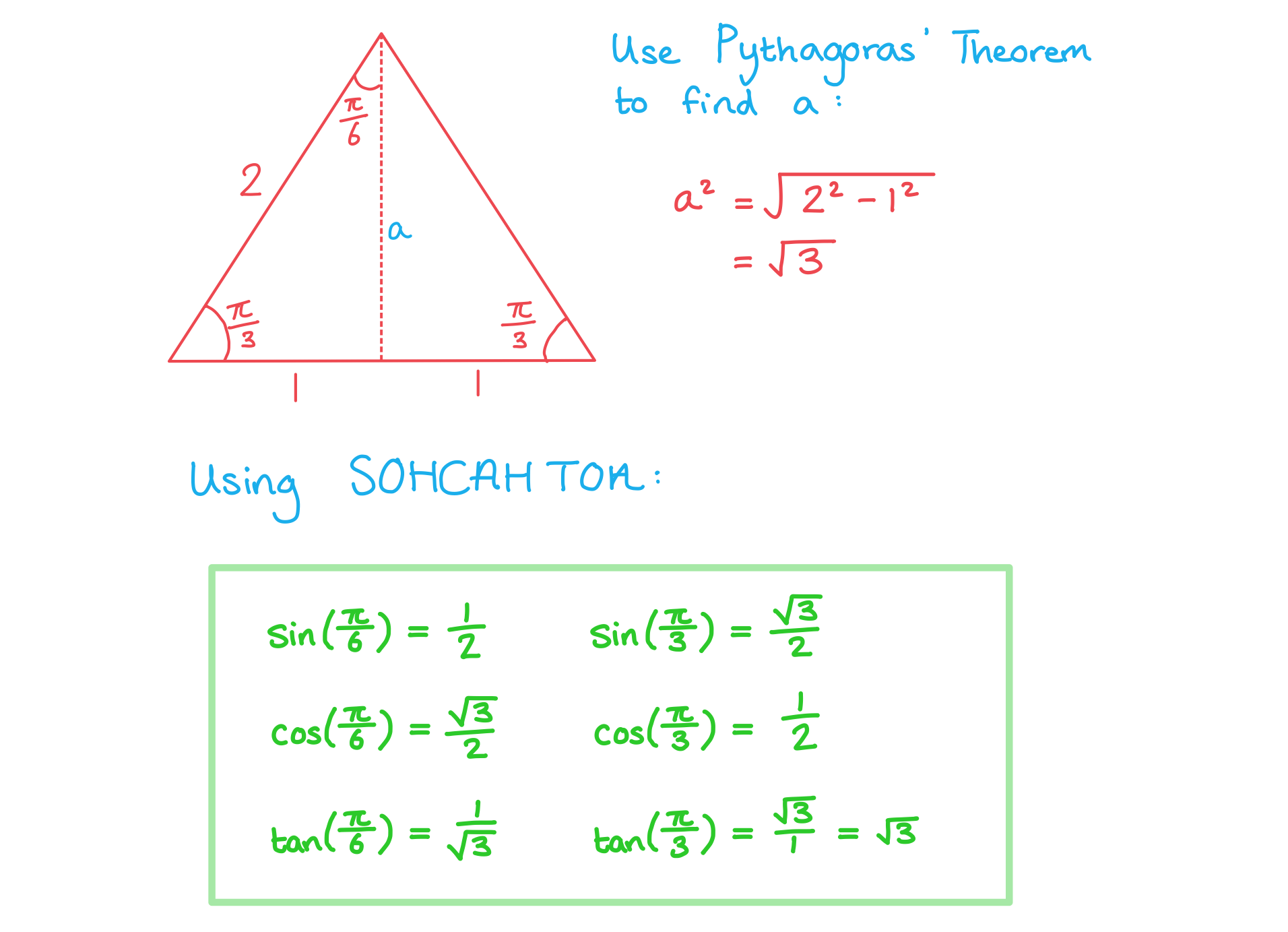
Using an equilateral triangle of side length 2 units, derive the exact values for the sine, cosine and tangent of and
.

Unlock more, it's free!
Was this revision note helpful?
