Graphs of Trigonometric Functions (Edexcel IGCSE Further Pure Maths)

Graphs of Trigonometric Functions

What are the graphs of trigonometric functions?

• The trigonometric functions sin, cos and tan all have special periodic graphs

  • periodic means the graphs repeat over certain intervals

• You need to know their properties and how to sketch them for a given domain

  • You must be able to do this for either degrees or radians

• Sketching the trigonometric graphs can help to

  • Solve trigonometric equations and find all solutions

  • Understand transformations of trigonometric functions

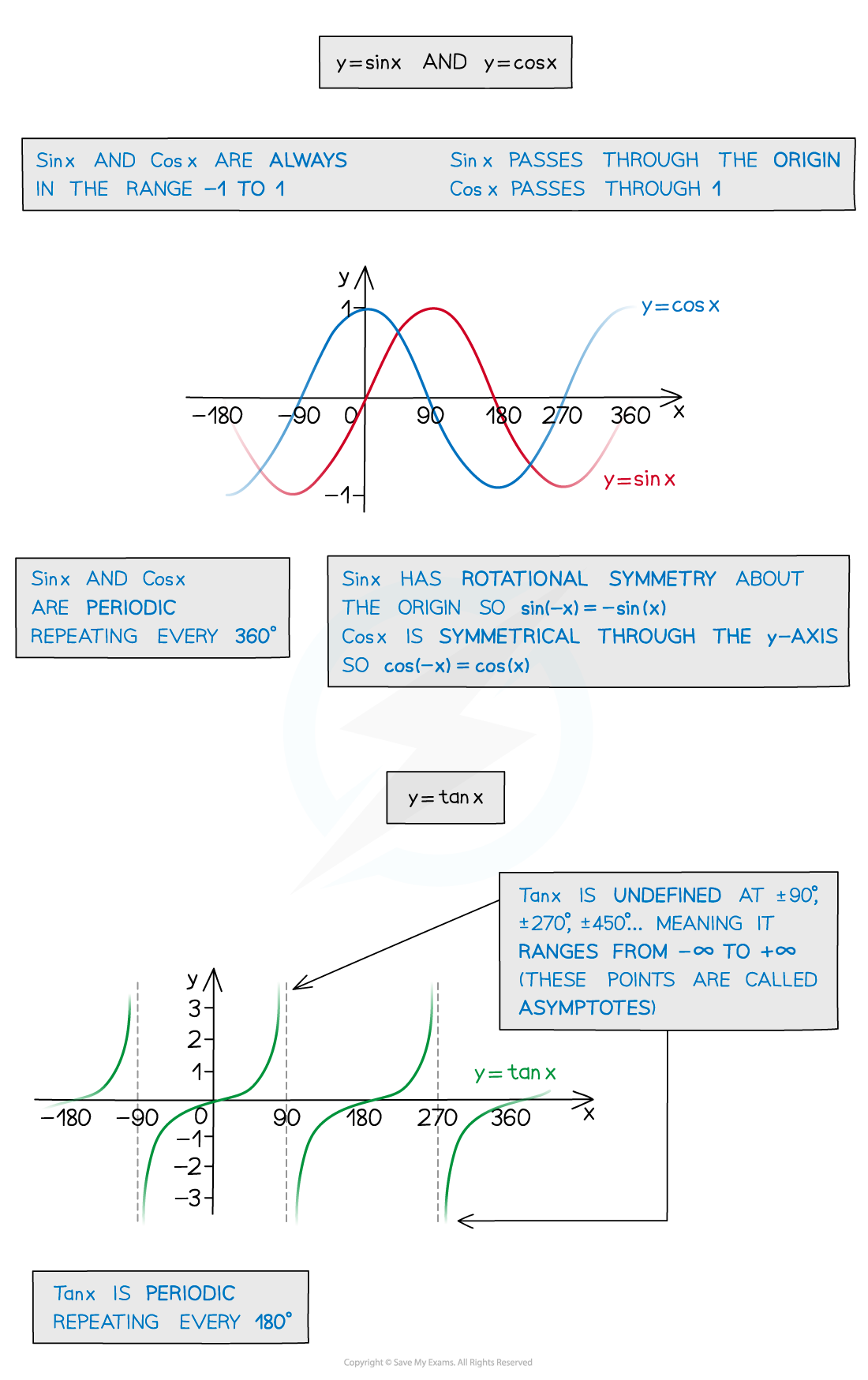
What are the properties of the graphs of sin x and cos x?

• The graphs of sin x and cos x are both periodic

  • They repeat every 360° (2π radians)

  • The angle measurement will always be on the x-axis

    • Either in degrees or radians

  • The corresponding value of the function will always be on the y-axis

• You need to know the domain and range of sin and cos

  • Domain: 

    • I.e. all real number values of x

    • Including 'angles' less than 0° and greater than less than 360°

  • Range: 

    • sin and cos can never take values greater than 1 or less than -1

  • The amplitude of the graphs of sin x  and cos x  is 1

• The graphs of sin x and cos x are translations of one other

  • sin x  passes through the origin (0, 0)

    • translate sin x  90° ( radians) to the left to get cos x

  • cos x  passes through (0, 1)

    • translate cos x  90° ( radians) to the right to get sin x

What are the properties of the graph of tan x?

• The graph of tan x  is periodic

  • It repeats every 180° (π radians)

  • The angle measurement will always be on the x-axis

    • Either in degrees or radians

• The graph of tan x  is undefined at ± 90°, ± 270° etc

  • There are vertical asymptotes at these points on the graph

  • In radians this is  radians, radians, etc

• You need to know the domain and range of tan

  • Domain: (degrees)  or  (radians)

    • I.e. all values (positive or negative) except where the asymptotes appear

  • Range: 

    • tan x  can take any real number value

How do I sketch trigonometric graphs?

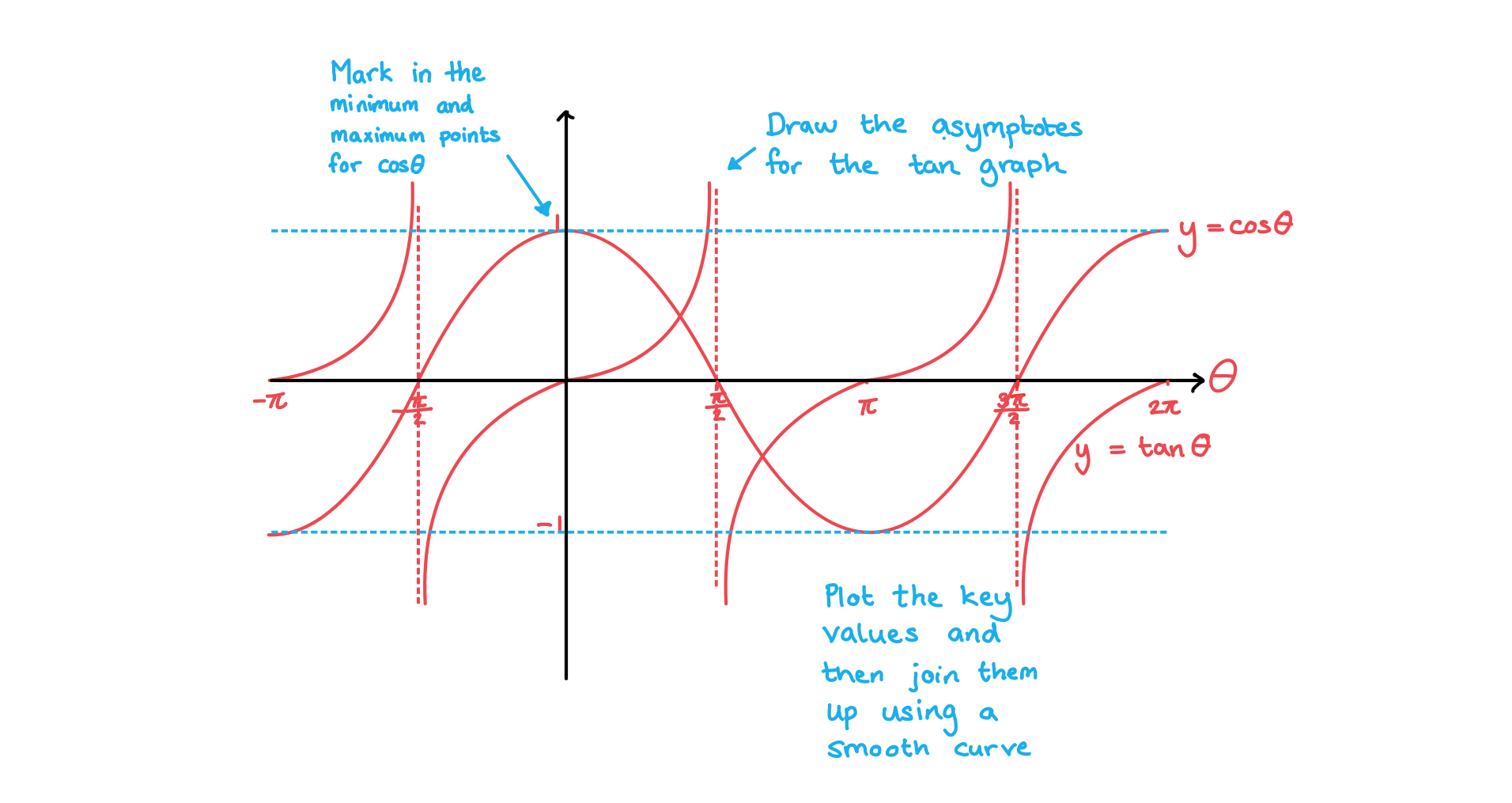
• You may need to sketch a trigonometric graph

  • so you will need to remember the key features of each one

• The following steps may help you sketch a trigonometric graph
  

• STEP 1
  Check whether you should be working in degrees or radians

• Check the interval given in the question

• If you see π  in the given interval then work in radians

• STEP 2 
  Label the x-axis in multiples of 90°

  • Or multiples of if you are working in radians

  • Make sure you cover the entire given interval on the x-axis

• STEP 3
  Label the y-axis

  • for sin x  or cos x

  • No specific points on the y-axis for tan x

• STEP 4
  Draw the graph

  • Knowing exact values will help with this

    • e.g. sin(0) = 0 and cos(0) = 1

  • Mark the important points on the axis first

  • If you are drawing the graph of tan x

    • put the asymptotes in first

  • If you are drawing sin x  or cos x

    • mark where the maximum and minimum points will be

  • Try to keep the symmetry (and rotational symmetry) as you sketch

    • This will help when using the graph to find solutions

Using Trigonometric Graphs

How can I use a trigonometric graph to find extra solutions?

• Your calculator will only give you one solution to an equation such as

  • This solution is called the primary value

• However sin, cos and tan are periodic

  • So there are an infinite number of solutions to an equation like  

• On the exam you will be given an interval in which your solutions should be found

  • This could either be in degrees or in radians

    • If you see π or some multiple of π then you must work in radians

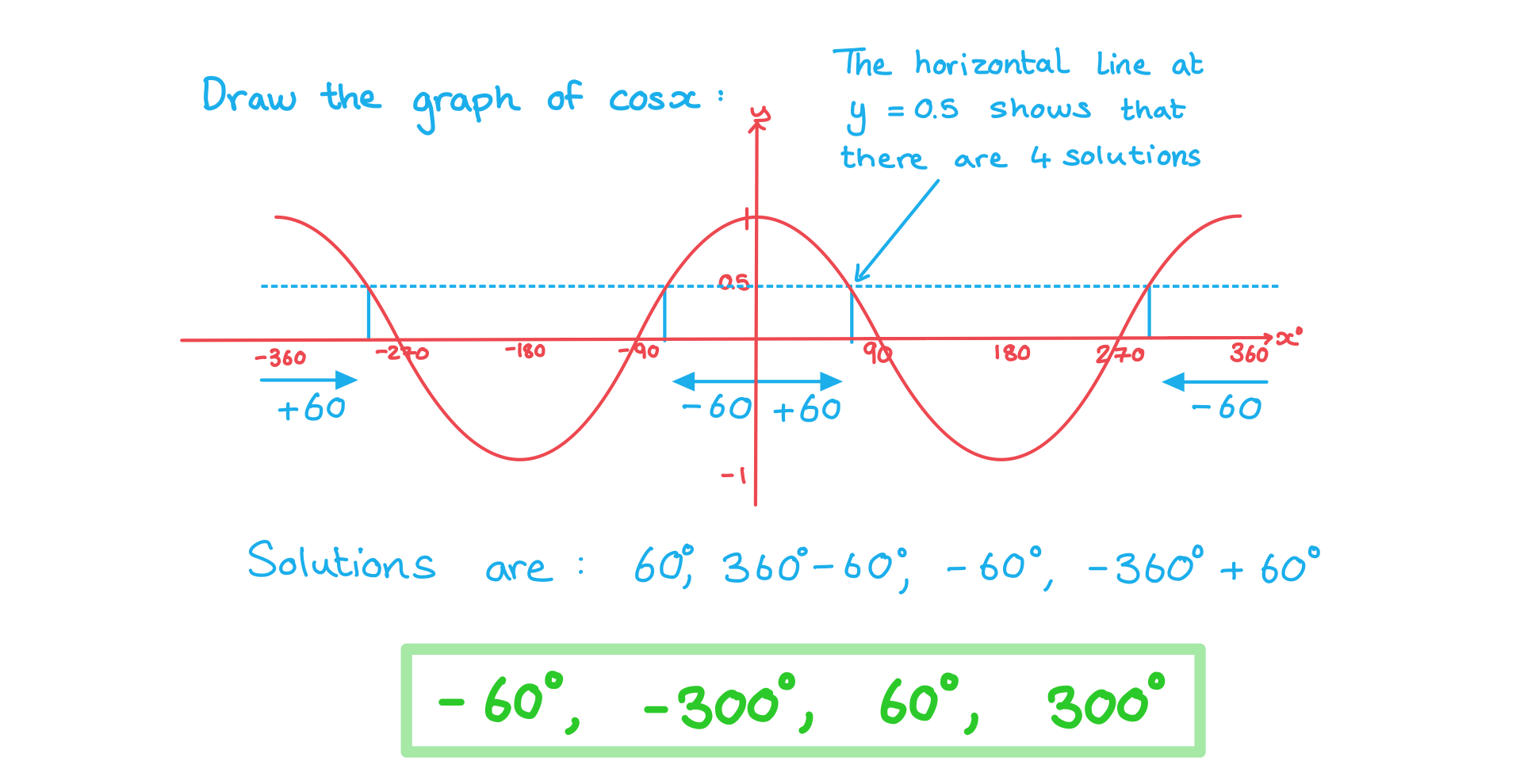
• The following steps will help you use the trigonometric graphs to find additional solutions
  
  

• STEP 1
  Sketch the graph for the given function and interval

  • Check whether you should be working in degrees or radians

  • Label the axes with the key values

• STEP 2
  Draw a horizontal line going through the y-axis at the value you are looking for

  • e.g. if you are looking for the solutions to 

    • then draw the horizontal line going through the y-axis at 

  • The number of times this line intersects the graph in the given interval

    • is the number of solutions within the interval

• STEP 3
  Find the primary value and mark it on the graph

  • It may be an exact value that you know

  • Or else you can use your calculator to find it

• STEP 4
  Use the symmetry of the graph to find all the solutions in the interval

  • This will involve adding or subtracting from the key values on the graph

What patterns can be seen from the graphs of trigonometric functions?

• The graph of sin x  has rotational symmetry about the origin

  • So

  • Also

    • or in radians

• The graph of cos x  has reflectional symmetry about the y-axis

  • So

  • Also

    • or in radians

• The graph of tan x  repeats every 180° (π radians)

  • So for 

    • or in radians

• The graphs of sin x  and cos x  repeat every 360° (2π radians)

  • So for 

    • or in radians

  • And for 

    • or in radians