IGCSEFurther MathsEdexcelRevision NotesGeometry & TrigonometryTrigonometric RatiosBasic Trigonometry

Basic Trigonometry (Edexcel IGCSE Further Pure Maths): Revision Note

Exam code: 4PM1

Amber

Written by: Amber

Reviewed by: Dan Finlay

Updated on

Right-Angled Trigonometry

What is right-angled trigonometry?

  • Right-angled trigonometry is the study of right-angled triangles

    • In particular the relationships between their side lengths and angles

  • Right-angled trigonometry includes two main components

    • The Pythagorean theorem

    • SOHCAHTOA

  • You should already be familiar with right-angled trigonometry from your regular IGCSE Mathematics course

What is the Pythagorean theorem?

  • The Pythagorean theorem (or Pythagoras’ theorem ) connects the side lengths in a right-angled triangle

    • It only works for right-angled triangles!

  • It says that for any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides

    • The hypotenuse is always the longest side in a right-angled triangle

      • It will always be opposite the right angle

  • If we label the hypotenuse c, and label the other two sides a and b, then

    • c squared equals a squared plus b squared

      • This is not on the exam formula sheet, so you need to remember it

  • This lets us find one side length if we know the other two side lengths

    • To find the hypotenuse

      • c equals square root of a squared plus b squared end root

    • To find one of the other two sides

      • a equals square root of c squared minus b squared end root  or  b equals square root of c squared minus a squared end root

  • Pythagoras' theorem can also be used to prove that a triangle is (or isn't) right-angled

    • If  c squared equals a squared plus b squared  is true for three side lengths a, b and c

      • then the triangle is right-angled

    • If  c squared equals a squared plus b squared  is not true for three side lengths a, b and c

      • then the triangle is not right-angled

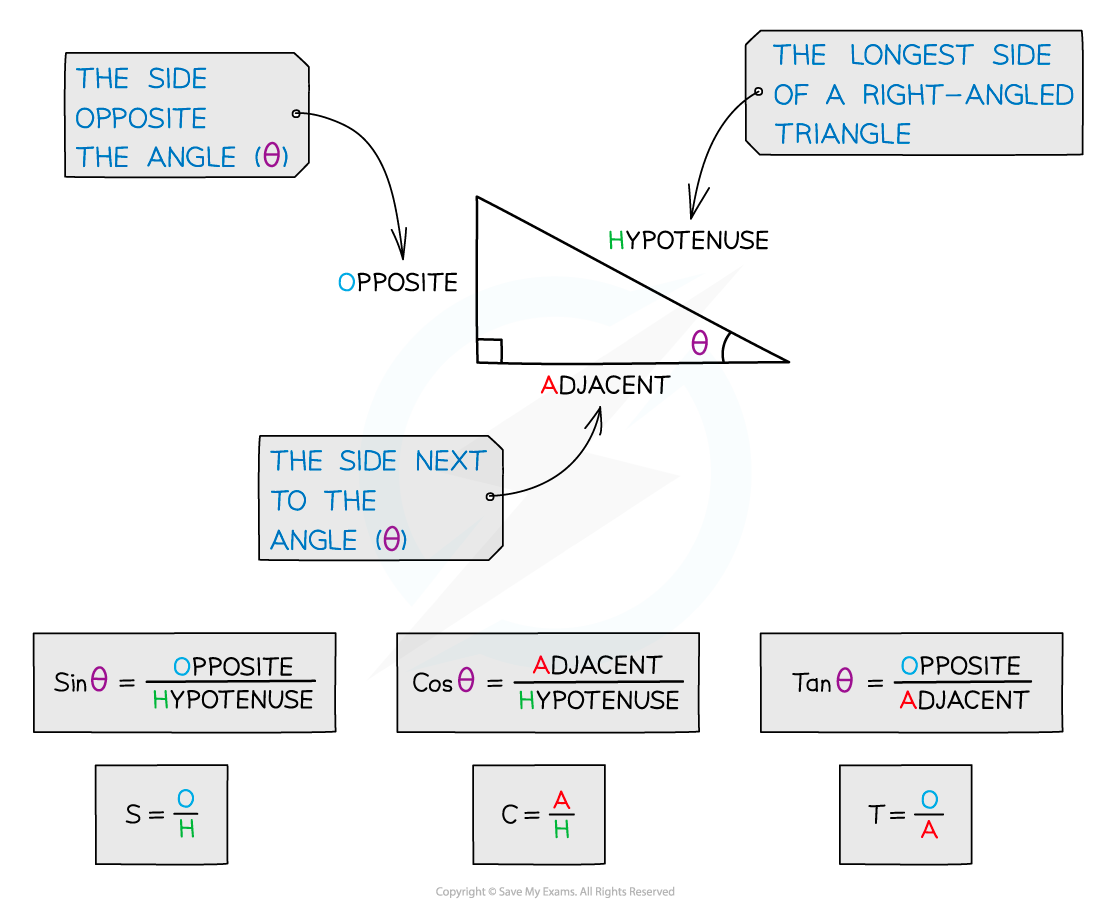
What is SOHCAHTOA?

  • SOHCAHTOA is a way to help remember the sine, cosine and tangent formulae for right-angled triangles

    • These formulae only work for right-angled triangles!

  • To use the formulae you must first label the sides of a right-angled triangle in relation to a chosen angle

    • The hypotenuse, H, is the longest side in a right-angled triangle

      • It will always be opposite the right angle

    • If we label one of the other angles θ,

      • the side opposite θ will be labelled opposite, O

      • and the side next to θ will be labelled adjacent, A

  • The SOHCAHTOA formulae are

    • Sin space theta blank equals space opposite over hypotenuse space equals space O over H  ('SOH')

    • Cos space theta blank equals space adjacent over hypotenuse space equals space straight A over straight H  ('CAH')

    • Tan space theta blank equals space opposite over adjacent space equals space straight O over straight A  ('TOA')

  • These are not on the exam formula sheet, you need to remember them

  • You can use SOHCAHTOA to find

    • an angle, if you know two side lengths

    • a side length, if you know an angle and another side length

  • Start by choosing the correct formula

    • It needs to include two things you know as well as the thing you want to know

  • Then substitute the values you know into the formula

    • and solve for the missing value

      • If finding an angle, you'll need to use sin to the power of negative 1 end exponent, cos to the power of negative 1 end exponent or tan to the power of negative 1 end exponent on your calculator

      • Or use your knowledge of exact trig values where possible

Opposite ,Hypotenuse, and Adjacent for Soh Cah Toa

Examiner Tips and Tricks

  • Make sure you know the formulae for the Pythagorean theorem and SOHCAHTOA

    • They are not given to you on the exam formula sheet

  • An exam question probably won't tell you to use the Pythagorean theorem or SOHCAHTOA

    • But think about them whenever you see a right-angled triangle in an exam!

Worked Example

A chocolate bar is in the shape of a triangular prism A B C D E F.  The end of the chocolate bar is an isosceles triangle, where A C equals 3 space cm and A B equals B C equals 5 space cm.  Point M is the midpoint of A C. This information is shown in the diagram below.

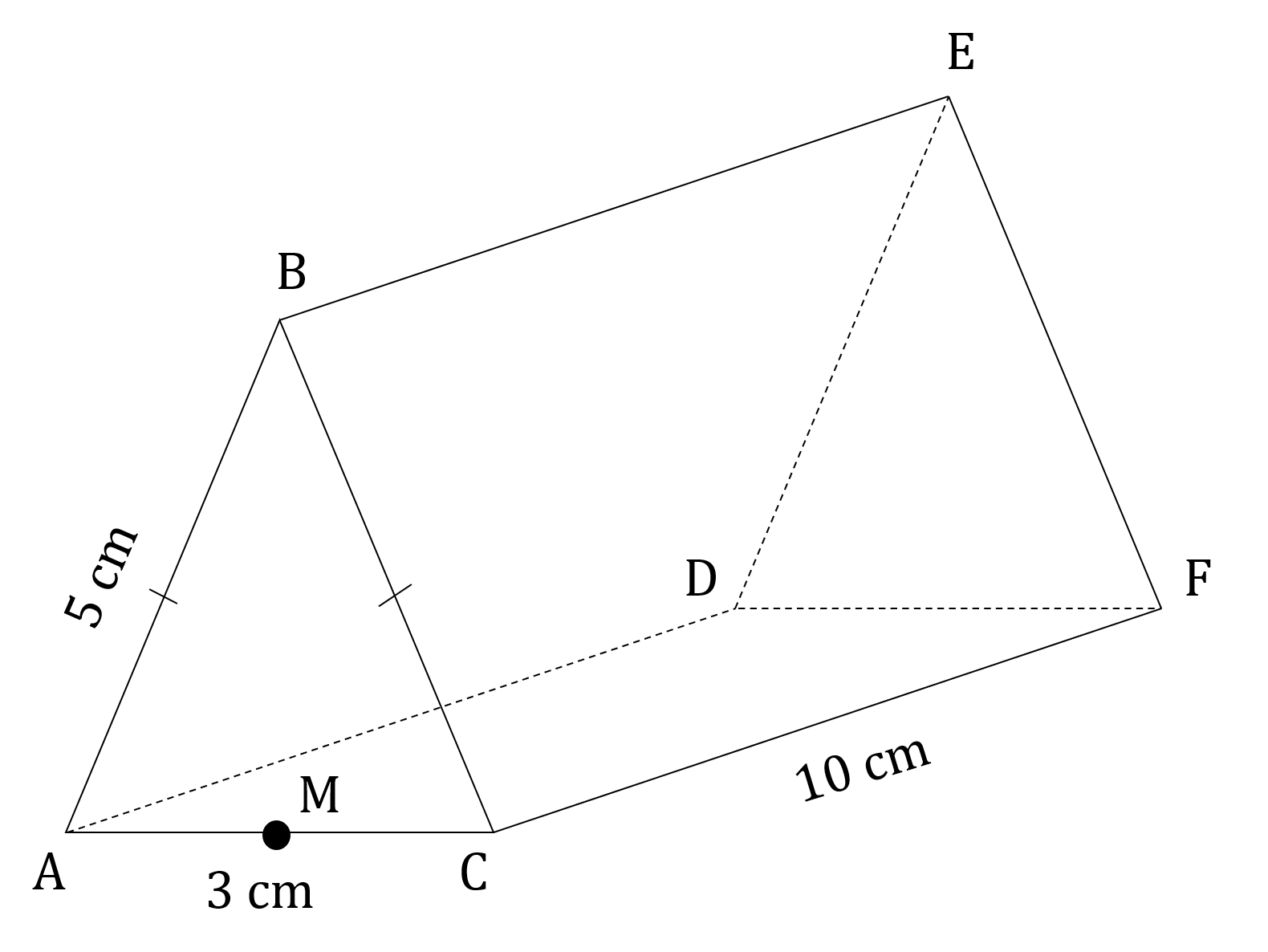
diagram-for-we-3-3-1-pythag

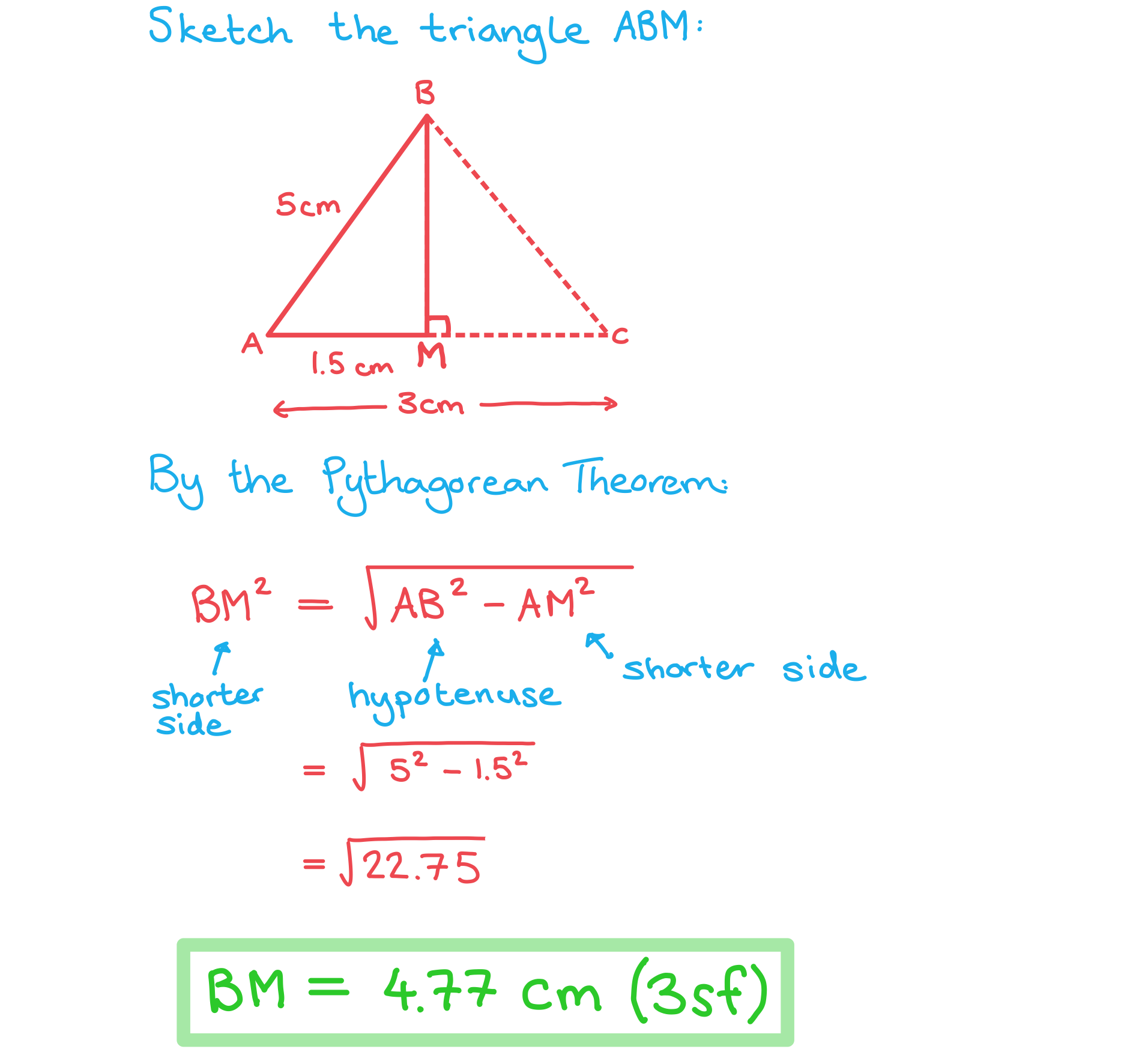
Calculate the length of BM, giving your answer correct to 3 significant figures.

3-3-1-ai-sl-pythag-we-solution

Worked Example

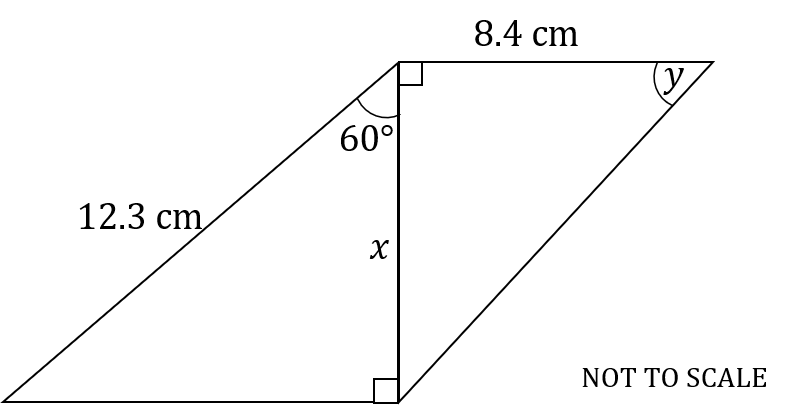
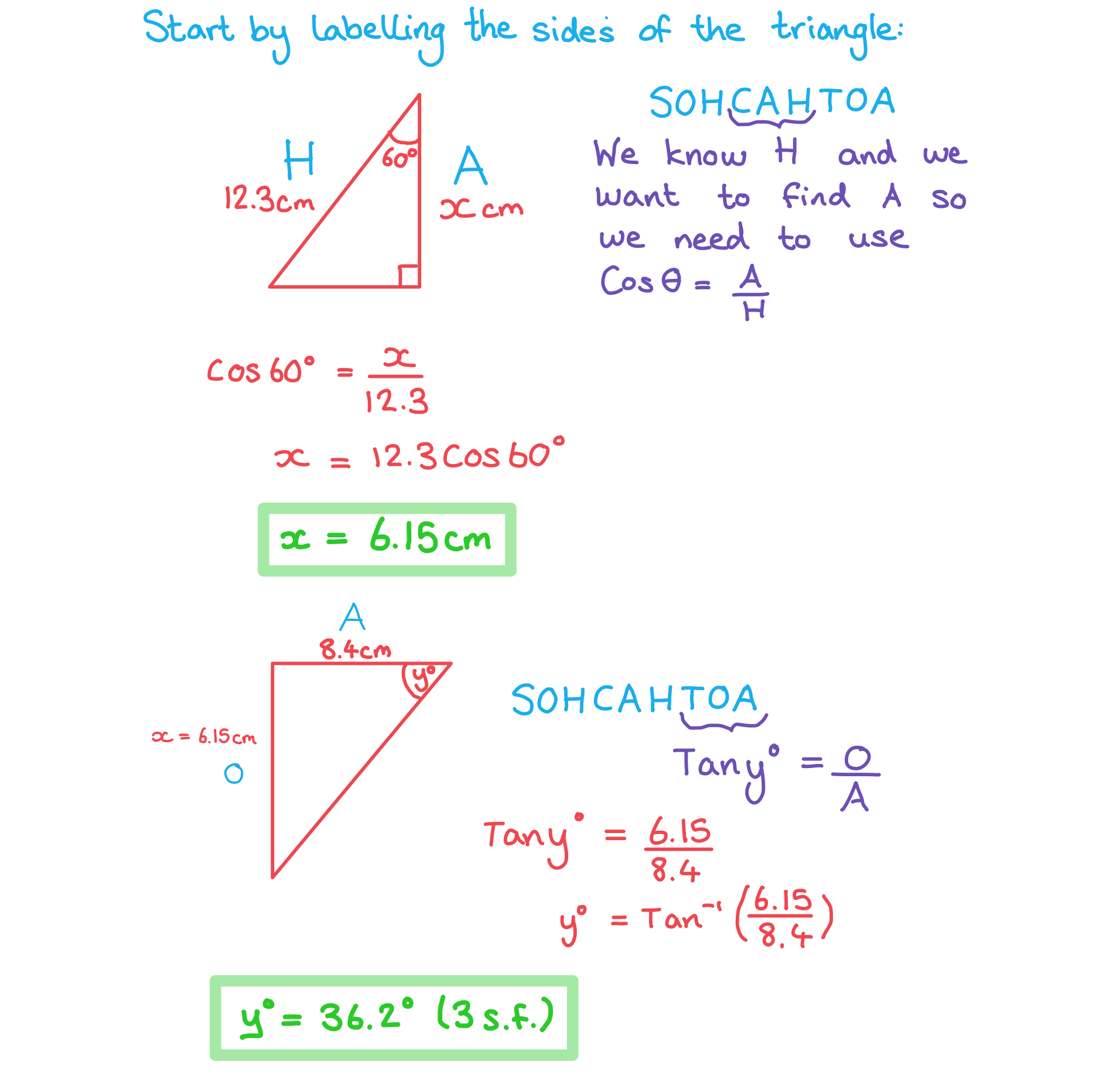
Find the values of x and y in the following diagram. Give your answers correct to 3 significant figures.

sa-diagram-for-we-3-3-1-trig
3-3-1-ai-sl-r-a-trig-we-solution

3D Problems

How does Pythagoras work in 3D?

  • 3D shapes can often be broken down into several 2D shapes

  • With Pythagoras’ Theorem you will be specifically looking for right-angled triangles

    • You need right-angled triangles with two known sides and one unknown side

    • Look for perpendicular lines to help you spot right-angled triangles

  • There is a 3D version of the Pythagorean theorem formula:

    • l squared space equals space x squared space plus space y squared space plus space z squared

      • l is the length of the line segment

      • x is the 'x-direction distance' between the endpoints of the line segment

      • y is the 'y-direction distance'

      • z is the 'z-direction distance' 

  • However it is usually easier to break a 3D problem down into two or more 2D problems

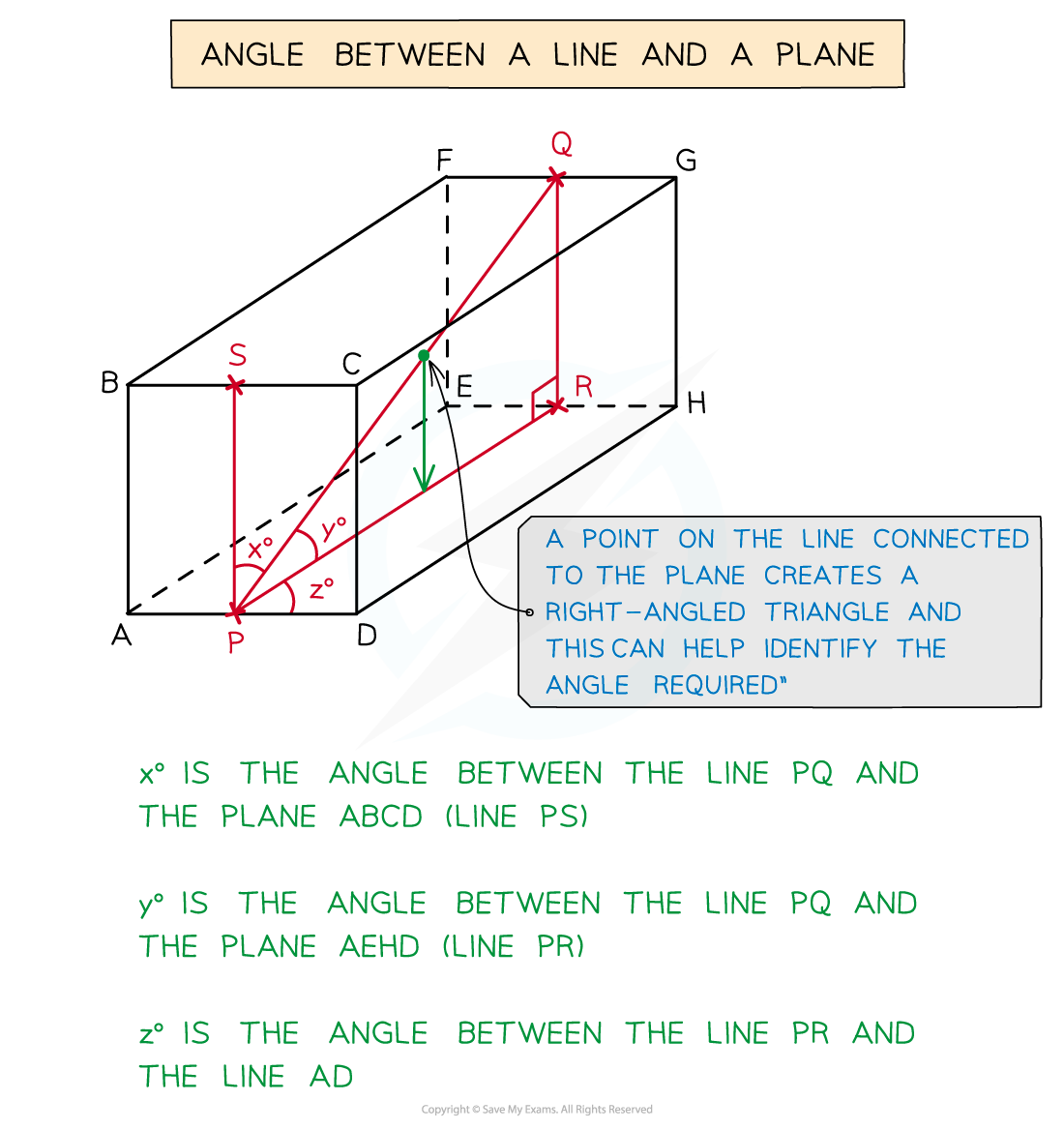
How does SOHCAHTOA work in 3D?

  • Again look for right-angled triangles including a missing angle or side

    • It may take more than one right-angles triangle to get to the answer

  • The angle you are working with can be awkward in 3D

    • The angle between a line and a plane is not always obvious

    • If unsure choose a point on the line and draw a new line to the plane

      • This should create a right-angled triangle

Trigonometry in 3d - within a cuboid

Examiner Tips and Tricks

  • Add values you have calculated to diagrams given in the question

  • Make additional sketches of parts of any diagrams that are given to you

    • Especially to help you 'see' a 2D portion of a 3D problem

  • If you are not given a diagram, sketch a nice, big, clear one!

Worked Example

A pencil is being put into a box in the shape of a cuboid with dimensions 3 cm by 4 cm by 6 cm.

Find:
 

(a) the length of the longest pencil that could fit inside the box,

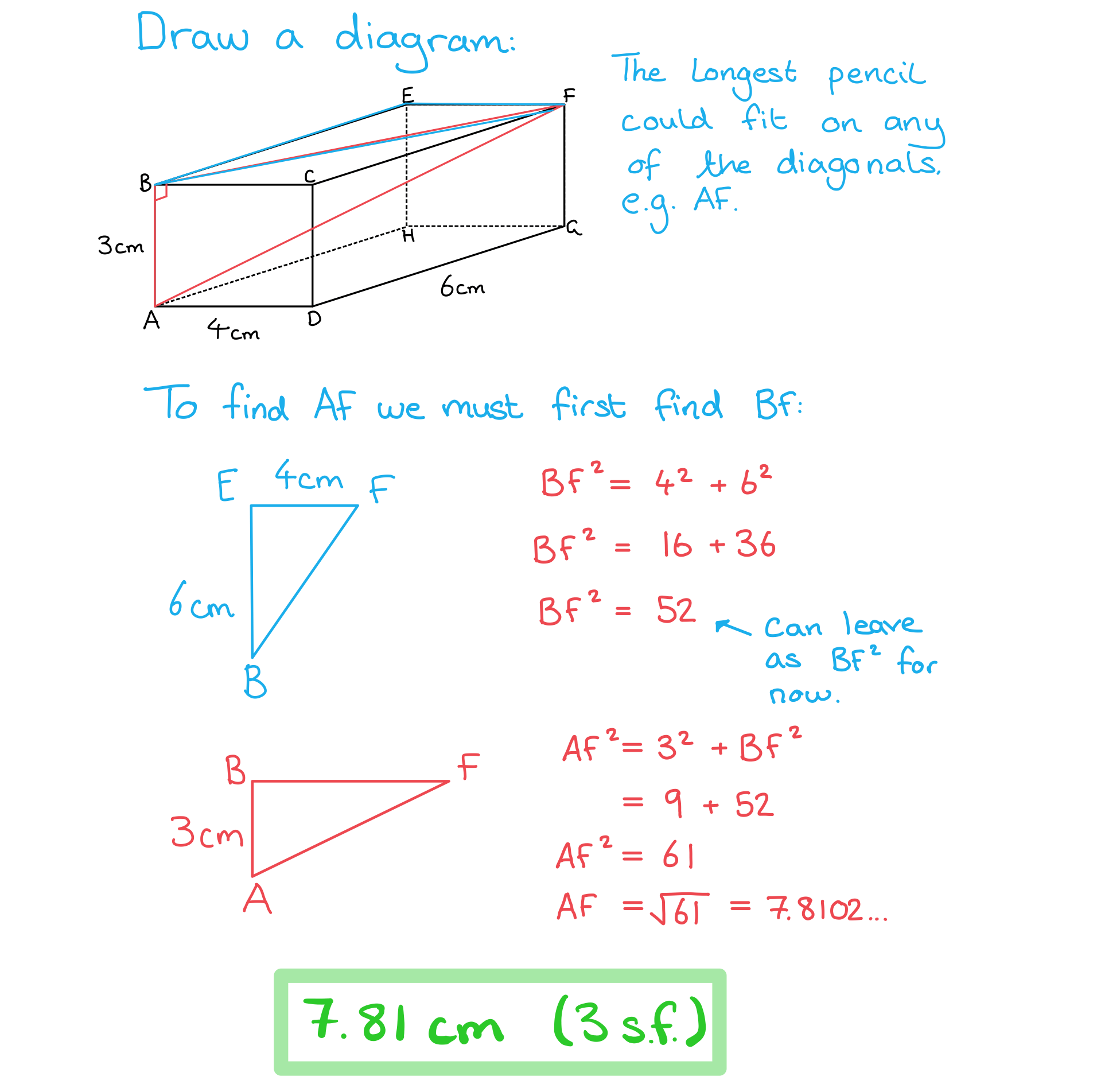
ai-sl-3-3-1-3d-pythag-trig-we-solution-a

 

(b) the angle that the pencil would make with the top of the box.

ai-sl-3-3-1-3d-pythag-trig-we-solution-b

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Previous:Arcs & SectorsNext:Sin, Cos & Tan
    Author
    Reviewer
    Amber

    Author: Amber

    Expertise: Maths Content Creator

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.