Sine & Cosine Formulae (Edexcel IGCSE Further Pure Maths): Revision Note
Exam code: 4PM1
Sine Formula
What is the sine formula?
The sine formula allows us to find missing side lengths or angles in non-right-angled triangles
It is also known as the sine rule
It states that for any triangle with angles A, B and C
a is the side opposite angle A
b is the side opposite angle B
c is the side opposite angle C
This formula is not on the exam formula sheet, so you need to remember it
Remember that sin 90° = 1
So if one of the angles is 90° this becomes SOH from SOHCAHTOA
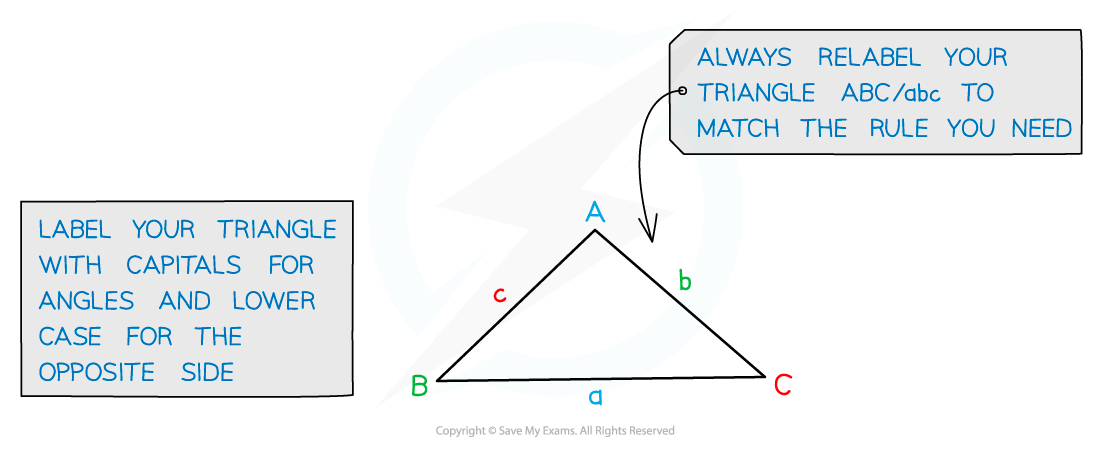
How can I use the sine formula to find missing side lengths or angles?
The sine formula can be used when you have any opposite pairs of sides and angles
Always start by labelling your triangle with the angles and sides
Remember
the sides with the lower-case letters
are opposite the angles with the equivalent upper-case letters
Use the formula as given above to find the length of a side
To find a missing angle it's easier to 'flip' the formula
Substitute the values you have into the formula and solve
This will always give you an acute angle
If you know the angle is obtuse then subtract this value from 180
Examiner Tips and Tricks
Remember to check that your calculator is in the correct angle mode (degrees or radians)!
Worked Example
The following diagram shows triangle .
,
, and angle
. It is also given that angle
is acute.
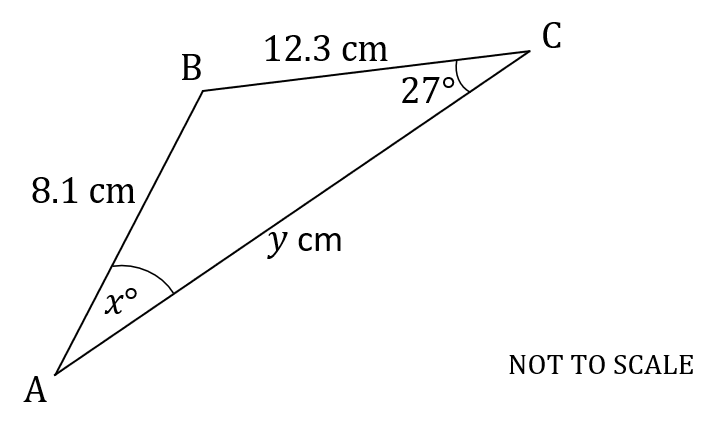
(a) Find the value of ,
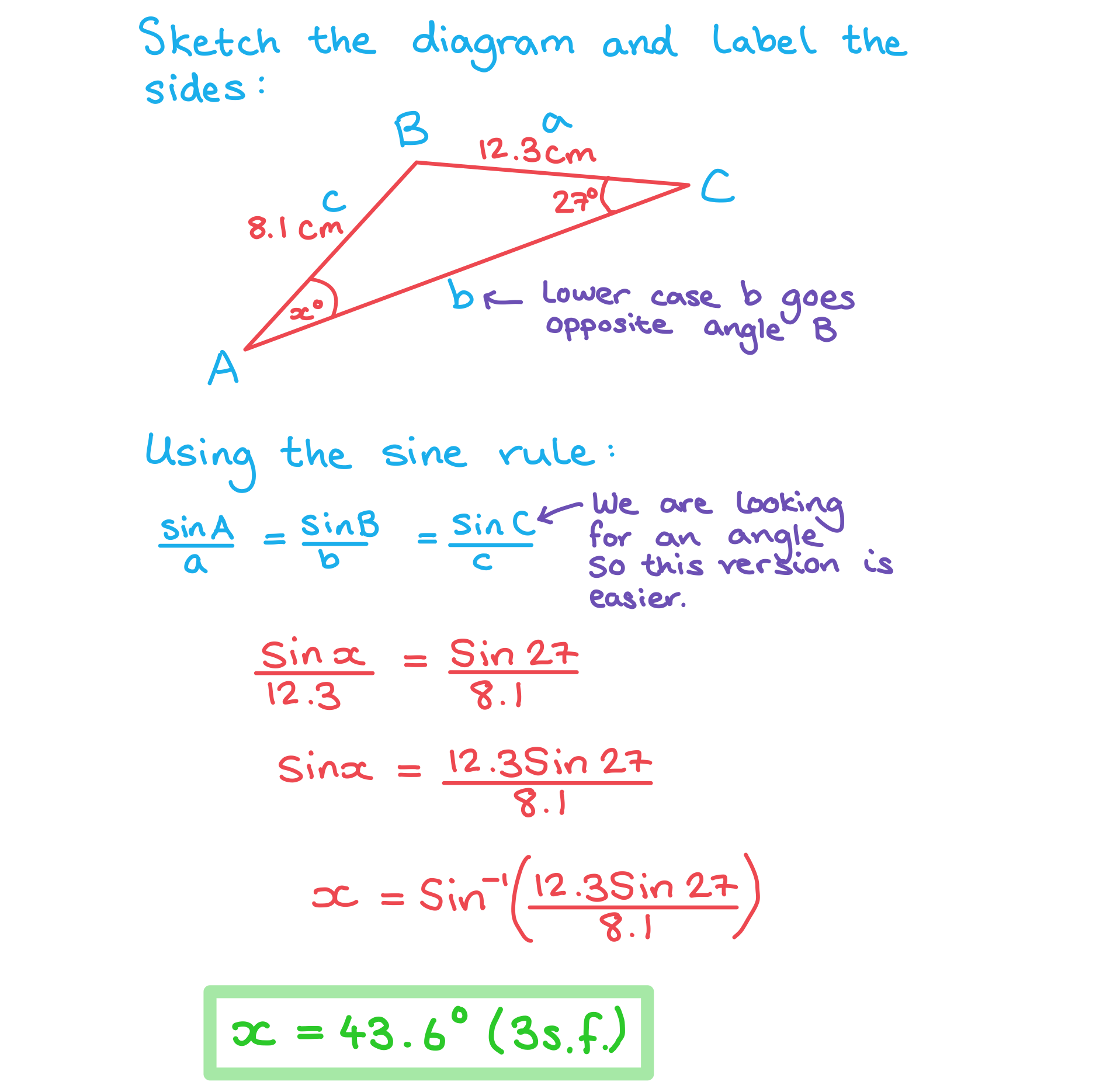
(b) Find the value of .

Cosine Formula
What is the cosine formula?
The cosine formula allows us to find missing side lengths or angles in non-right-angled triangles
It is also known as the cosine rule
It states that for any triangle
a is the side opposite angle A
b and c are the other two sides
angle A is the angle in between sides b and c
This formula is on the exam formula sheet
So you don't need to remember it
But you do need to be able to use it
Remember cos 90° = 0
So if A = 90° this becomes Pythagoras’ Theorem
How can I use the cosine formula to find missing side lengths or angles?
The cosine rule can be used when you have two sides and the angle between them or all three sides
Always start by labelling your triangle with the angles and sides
Remember
the sides with the lower-case letters
are opposite the angles with the equivalent upper-case letters
Use the formula in the formula sheet form to find an unknown side
Rearrange the formula to find an unknown angle
Remember, A must be the angle in between sides b and c
Substitute the values you have into the formula and solve
Examiner Tips and Tricks
Remember to check that your calculator is in the correct angle mode (degrees or radians)!
Worked Example
The following diagram shows triangle .
,
, and
.

Calculate the size of angle .

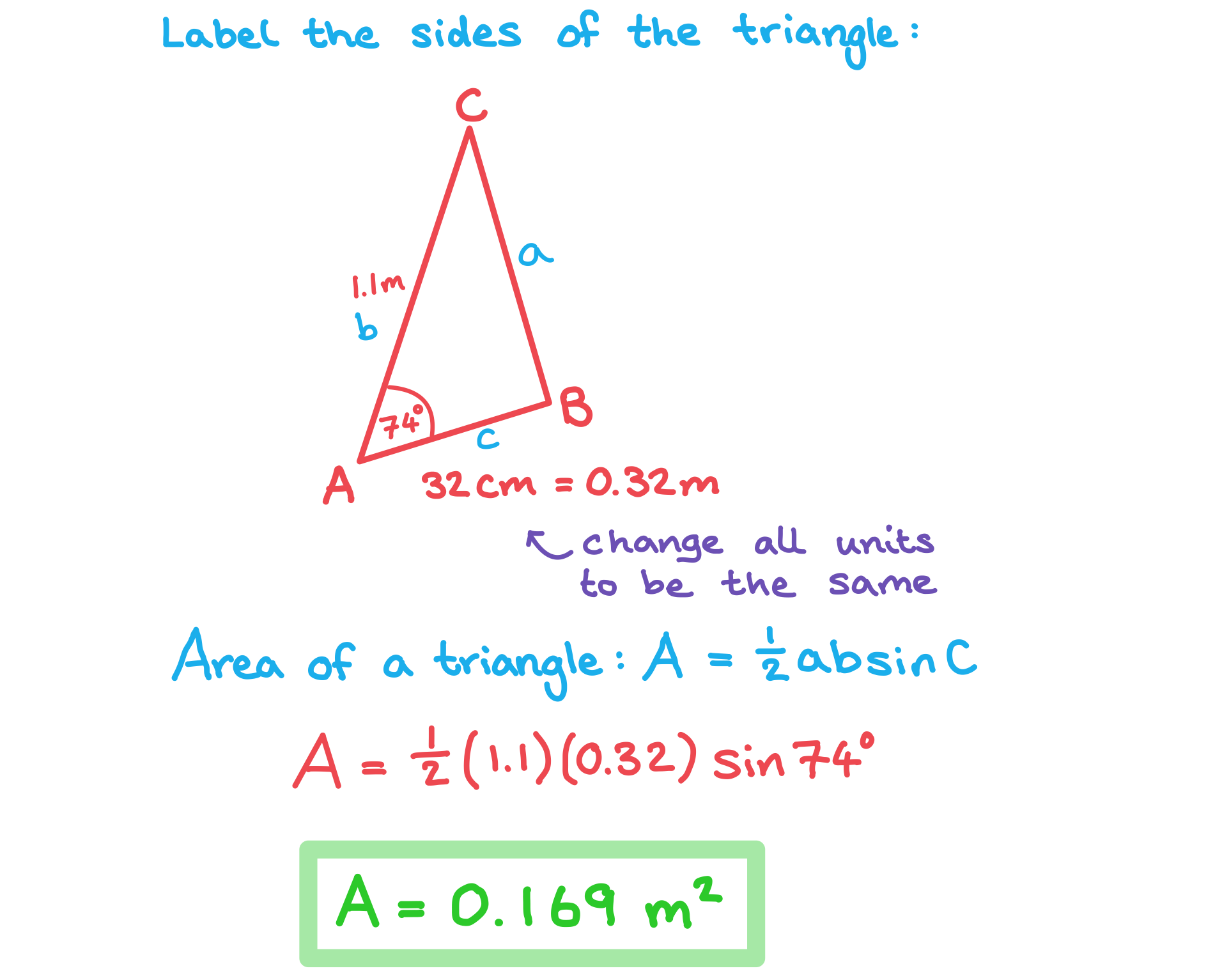
Area of a Triangle
How do I find the area of a non-right-angled triangle?
The area of any triangle can be found using the formula
C is the angle in between sides a and b
This formula is not on the exam formula sheet, so you need to remember it
Remember sin 90° = 1
so if C = 90° this becomes Area = ½ × base × height
If you know the area you can use the formula to find the length of a side or an angle
Using inverse sin will always give you an acute angle
Subtract the value from 180 if you know the angle is obtuse
Examiner Tips and Tricks
Be careful to label your triangle correctly
so that your angle C is always the angle between the two sides
Remember to check that your calculator is in the correct angle mode (degrees or radians)!
Worked Example
The following diagram shows triangle .
,
, and angle
.
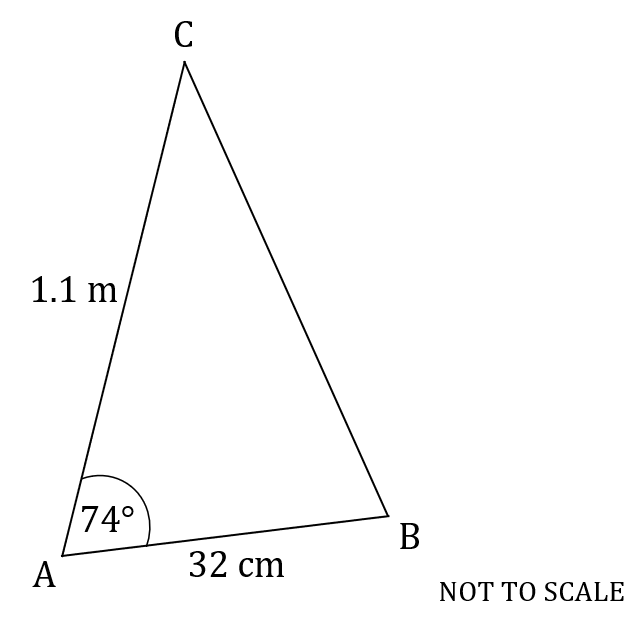
Calculate the area of triangle, giving your answer correct to 3 significant figures.

Unlock more, it's free!
Did this page help you?