IGCSEFurther MathsEdexcelRevision NotesGeometry & TrigonometryTrigonometric EquationsLinear Trigonometric Equations

Linear Trigonometric Equations (Edexcel IGCSE Further Pure Maths)

Revision Note

Amber

Written by: Amber

Reviewed by: Dan Finlay

Linear Trigonometric Equations

How do I solve trigonometric equations?

  • Trigonometric equations can have an infinite number of solutions

    • For an equation in bold sin bold italic x or bold cos bold italic x

      • you can add or subtract 360° (or 2π radians) to each solution to find more solutions

    • For an equation in bold tan bold italic x

      • you can add or subtract 180° (or π radians) to each solution to find more solutions

  • When solving a trigonometric equation

    • You will be given a interval of values within which the answers must lie

      • You need to find all the answers within that range

    • Using the inverse function on your calculator will only give you the primary value

      • This may or may not be in the required interval

    • The other values can be found with the help of:

      • your knowledge of trigonometric exact values

      • the unit circle

      • the graphs of trigonometric functions

How are basic trigonometric equations solved?

  • This means equations in the form  bold sin bold italic x bold equals bold italic k, bold cos bold italic x bold equals bold italic k  or  bold tan bold italic x bold equals bold italic k

  • It can be helpful to sketch the graph of the trigonometric function first

    • Use the given interval of values as the domain for your graph

    • The intersections of the graph of the function and the line y equals k will show you

      • The location of the solutions

      • The number of solutions

    • You will be able to use the symmetry properties of the graph to find other values within the given interval

The methods for finding all solutions are:

  • For the equation bold sin bold italic x bold equals bold italic k

    • The primary value is x subscript 1 equals sin to the power of negative 1 end exponent k

    • By symmetry, a secondary value is x subscript 2 equals 180 degree minus sin to the power of negative 1 end exponent k

      • Either x subscript 1 or x subscript 2 might not actually be in the given interval!  

    • Then all values within the given interval can be found using

      • x subscript 1 plus-or-minus 360 n degree

      • x subscript 2 plus-or-minus 360 n degree

      • where  n equals 1 comma space 2 comma space 3 comma space...  as appropriate

  • For the equation bold cos bold italic x bold equals bold italic k

    • The primary value is x subscript 1 equals cos to the power of negative 1 end exponent k 

    • By symmetry, a secondary value is x subscript 2 equals negative cos to the power of negative 1 end exponent k

      • Either x subscript 1 or x subscript 2 might not actually be in the given interval!

    • Then all values within the given interval can be found using

      • x subscript 1 plus-or-minus 360 n degree

      • x subscript 2 plus-or-minus 360 n degree

      • where  n equals 1 comma space 2 comma space 3 comma space...  as appropriate

  • For the equation bold tan bold italic x bold equals bold italic k 

    • The primary value is x subscript 1 equals tan to the power of negative 1 end exponent k

      • x subscript 1 might not actually be in the given interval!

    • Then all values within the given interval can be found using

      • x plus-or-minus 180 n degree

      • where  n equals 1 comma space 2 comma space 3 comma space...  as appropriate 

How do I handle more complicated equations?

  • You may need to use algebra to get an equation into one of the basic forms

  • For example, sin x tan x minus 3 sin x plus tan x equals 3

    • Subtract 3 from both sides

      • sin x tan x minus 3 sin x plus tan x minus 3 equals 0

    • Factorise

      • open parentheses sin x plus 1 close parentheses open parentheses tan x minus 3 close parentheses equals 0

    • This gives you two basic equations to solve

      • sin x equals negative 1

      • tan x equals 3

  • Trigonometric identities and/or addition formulae may also be needed

Examiner Tips and Tricks

  • Remember that your calculator will only give you the primary value

    • You need to be able to find all other solutions within the given interval

  • Sketching the trig graphs (or any other useful diagrams) can be a huge help!

Worked Example

Solve the equation  2 cos space x space equals space minus 1,  finding all solutions in the interval  negative 2 pi space less or equal than space x space less or equal than 2 space pi.

First isolate cos x

cos x equals negative 1 half

Use calculator or knowledge of exact trig values to find x subscript 1
Note that the interval is given in radians, so we must work in radians!

x subscript 1 equals cos to the power of negative 1 end exponent open parentheses negative 1 half close parentheses equals fraction numerator 2 pi over denominator 3 end fraction

Use symmetry of the cos function to find x subscript 2

x subscript 2 equals negative x subscript 1 equals negative fraction numerator 2 pi over denominator 3 end fraction

Now add or subtract (multiples of) 2 pi radians to find other solutions in the interval

x subscript 1 minus 2 pi equals fraction numerator 2 pi over denominator 3 end fraction minus 2 pi equals negative fraction numerator 4 pi over denominator 3 end fraction

x subscript 2 plus 2 pi equals negative fraction numerator 2 pi over denominator 3 end fraction plus 2 pi equals fraction numerator 4 pi over denominator 3 end fraction


Any other additions or subtractions of 2 pi would take us outside the interval

bold italic x bold equals bold minus fraction numerator bold 4 bold pi over denominator bold 3 end fraction bold comma bold space bold minus fraction numerator bold 2 bold pi over denominator bold 3 end fraction bold comma bold space fraction numerator bold 2 bold pi over denominator bold 3 end fraction bold comma bold space fraction numerator bold 4 bold pi over denominator bold 3 end fraction

Linear Trigonometric Equations (ax + b)

How can I solve equations with transformations of trig functions?

  • This means equations of the form sin(ax+b) = k,  cos(ax+b) = k  or  tan(ax+b) = k 

    • Trigonometric equations in these forms can be solved in more than one way

  • The easiest method is to consider the transformation of the angle as a substitution

    • Let u = ax + b

  • Transform the given interval for the solutions in the same way as the angle

    • For example if the given interval is  0° ≤ x ≤ 360°  the new interval will be

      • (a (0°) + b) ≤ u ≤ (a (360°) + b)

  • Solve the equation to find the primary value for u

  • Find all the other solutions in the transformed range for u

  • Undo the substitution

    • i.e.  x equals fraction numerator u minus b over denominator a end fraction

    • Convert all of the u solutions back into corresponding solutions for x

  • Another method would be to sketch the transformation of the function

    • If you use this method then you will not need to use a substitution for the range of values

Examiner Tips and Tricks

  • If you use substitution and transform the interval

    • remember to convert answers back at the end!

Worked Example

Solve the equation  2 cos left parenthesis 2 x minus 30 degree right parenthesis equals negative 1,  finding all solutions in the interval  negative 360 degree less or equal than x less or equal than 360 degree.

We'll use the substitution  u equals 2 x minus 30

Let space u equals 2 x minus 30


Rewrite the equation in terms of u and rearrange


table row cell 2 cos u end cell equals cell negative 1 end cell row cell cos u end cell equals cell negative 1 half end cell end table


Now we need to transform the interval as well
Substitute the interval limits into  u equals 2 x minus 30

2 open parentheses negative 360 close parentheses minus 30 equals negative 750

2 open parentheses 360 close parentheses minus 30 equals 690

negative 750 degree less or equal than u less or equal than 690 degree

Use calculator or knowledge of exact trig values to find the primary value

u subscript 1 equals cos to the power of negative 1 end exponent open parentheses negative 1 half close parentheses equals 120


Use symmetry of cos function to find the secondary value

u subscript 2 equals negative u subscript 1 equals negative 120


Sketch the graph of cos u over the transformed interval

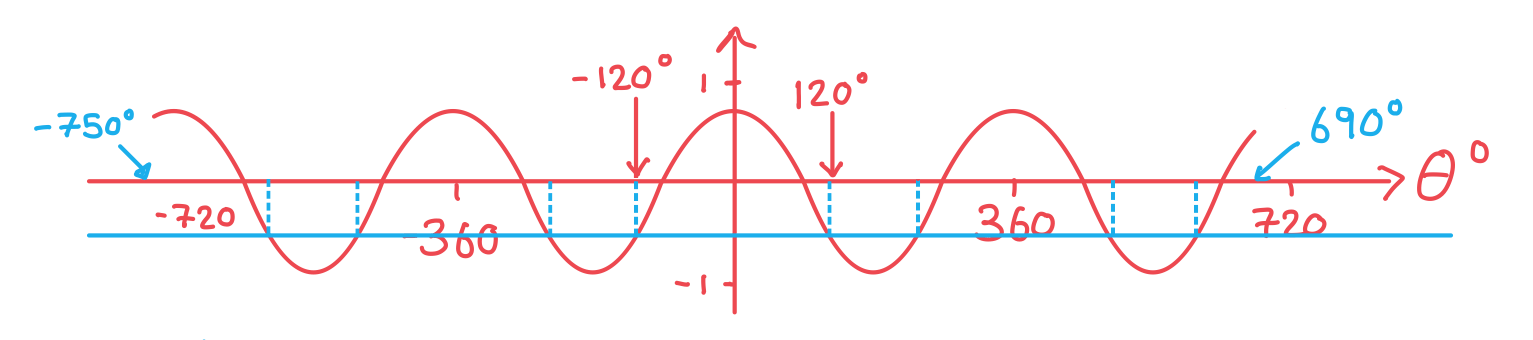
cxVOKRsE_igcse-fpure-trig-eqns-we

This shows that there are 8 places where cos u equals negative 1 half

Find these by adding or subtracting (multiples of) 360 degree to u subscript 1 and u subscript 2

u equals negative 600 comma space minus 480 comma space minus 240 comma space minus 120 comma space 120 comma space 240 comma space 480 comma space 600

Invert the substitution

table row u equals cell 2 x minus 30 end cell row cell 2 x end cell equals cell u plus 30 end cell row x equals cell fraction numerator u plus 30 over denominator 2 end fraction end cell end table

Substitute the u values into  x equals fraction numerator u plus 30 over denominator 2 end fraction to find the corresponding x values


bold italic x bold equals bold minus bold 285 bold degree bold comma bold space bold minus bold 225 bold degree bold comma bold space bold minus bold 105 bold degree bold comma bold space bold minus bold 45 bold degree bold comma bold space bold 75 bold degree bold comma bold space bold 135 bold degree bold comma bold space bold 255 bold degree bold comma bold space bold 315 bold degree

Last updated:

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Trigonometric Addition FormulaeNext:Quadratic Trigonometric Equations
    Author
    Reviewer
    Amber

    Author: Amber

    Expertise: Maths

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.