Roots of Quadratic Equations (Edexcel IGCSE Further Pure Maths)

Revision Note

Written by: Roger B

Reviewed by: Dan Finlay

Discriminants

What is the discriminant of a quadratic function?

The discriminant of a quadratic is often denoted by the Greek letter $Δ$ (upper case delta)
For a quadratic $a x^{2} + b x + c (a \neq 0)$ the discriminant is given by
- $Δ = b^{2} - 4 a c$
The discriminant is the expression that is inside the square root in the quadratic formula
- $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
This is not on the exam formula sheet so you need to remember it

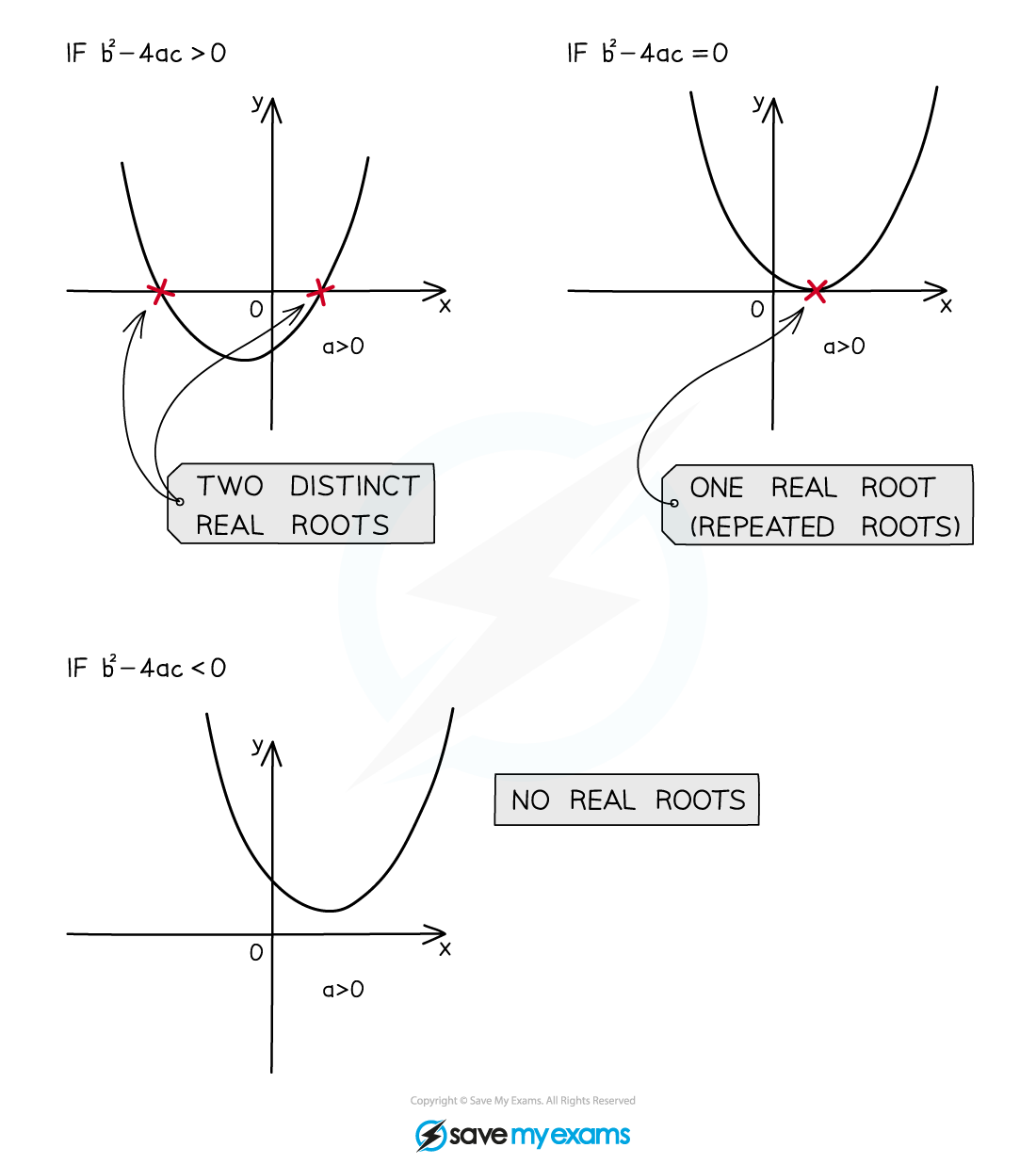
How does the discriminant of a quadratic function affect its graph and roots?

The discriminant tells us about the roots (or solutions) of the equation $a x^{2} + b x + c = 0$
- It also tells us about the graph of $y = a x^{2} + b x + c$
If Δ > 0 then $\sqrt{b^{2} - 4 a c}$ and $- \sqrt{b^{2} - 4 a c}$ are two distinct values
- The equation $a x^{2} + b x + c = 0$ has unequal real roots
  - i.e. there are two distinct real solutions
- The graph of $y = a x^{2} + b x + c$ crosses the x-axis twice
If $Δ = 0$ then $\sqrt{b^{2} - 4 a c}$ and $- \sqrt{b^{2} - 4 a c}$ are both zero
- The equation $a x^{2} + b x + c = 0$ has equal real roots
  - i.e. it has one repeated real solution
- The graph of $y = a x^{2} + b x + c$ touches the x-axis at exactly one point
  - This means that the x-axis is a tangent to the graph
If $Δ < 0$ then $\sqrt{b^{2} - 4 a c}$ and $- \sqrt{b^{2} - 4 a c}$ are both undefined
- The roots of the equation $a x^{2} + b x + c = 0$ are not real
  - i.e. it has no real solutions
- The graph of $y = a x^{2} + b x + c$ never touches the x-axis
  - This means that graph is wholly above (or below) the x-axis

How do I solve problems using the discriminant?

Often at least one of the coefficients of a quadratic will be given as an unknown
- For example the letter $k$ may be used for the unknown constant
You will be given a fact about the quadratic such as:
- The number of real solutions of the equation
- The number of roots (i.e. x-intercepts) of the graph
To find the value or range of values of $k$
- Find an expression for the discriminant
  - Use $Δ = b^{2} - 4 a c$
- Decide whether $Δ > 0$ , $Δ = 0$ or $Δ < 0$
  - If the question says there are real roots but does not specify how many then use $Δ \geq 0$
- Solve the resulting equation or inequality for $k$

Examiner Tips and Tricks

Questions won't always use the word discriminant
- It is important to recognise when its use is required
- Look for
  - a number of roots or solutions being stated
  - whether and/or how often the graph of a quadratic function intercepts the $x$ -axis

Worked Example

A function is given by $f (x) = 2 k x^{2} + k x - k + 2$ , where $k$ is a constant. The graph of $y = f (x)$ intercepts the $x$ -axis at two different points.

a) Show that $9 k^{2} - 16 k > 0$ .

The question says the graph 'intercepts the x-axis at two different points'

This means that the discriminant $b^{2} - 4 a c$ is greater than zero

Here $a = 2 k$ , $b = k$ , and $c = - k + 2$

${(k)}^{2} - 4 (2 k) (- k + 2) > 0$

Expand the brackets and collect terms

$\begin{array}{rcl} k^{2} - 8 k (- k + 2) & > & 0 \\ k^{2} + 8 k^{2} - 16 k & > & 0 \end{array}$

$9 k^{2} - 16 k > 0$

b) Hence find the range of possible values of $k$ .

Solve the inequality, beginning by factorising

$k (9 k - 16) > 0$

This tells us the graph of $y = 9 k^{2} - 16 k$ intercepts the horizontal axis at $k = 0$ and $k = \frac{16}{9}$

It can be helpful to sketch a graph here

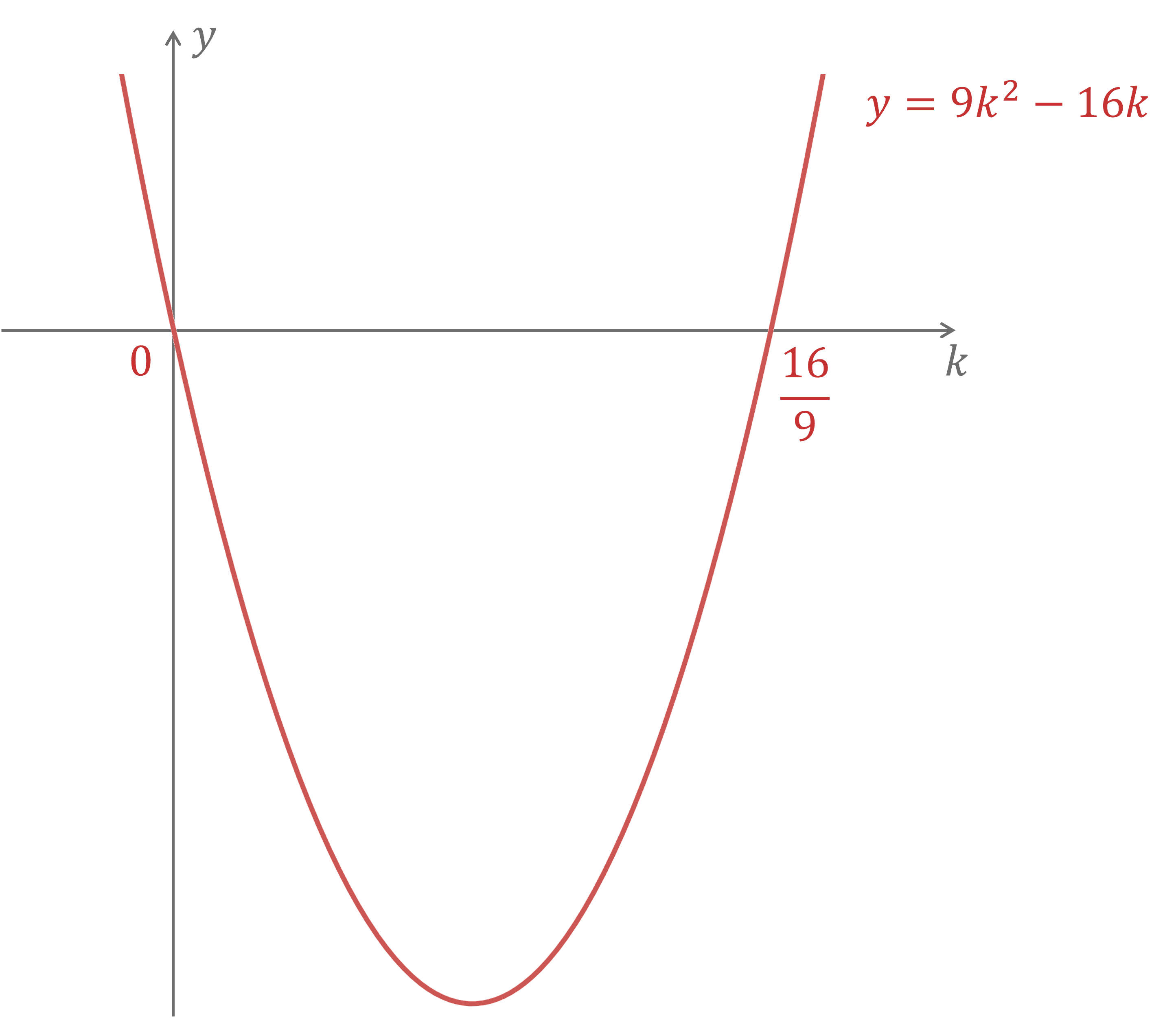
$9 k^{2} - 16 k > 0$ will be true to the left of 0 and to the right of $\frac{16}{9}$

Write these down as inequalities

$k < 0 or k > \frac{16}{9}$

Sum & Product of Roots

How are the roots of a quadratic equation linked to its coefficients?

A quadratic equation $a x^{2} + b x + c = 0$ (where $a \neq 0$ ) has roots $α$ and $β$ given by
- $α, β = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
  - i.e. the solutions found by the quadratic formula (or any other solution method)
This means the equation can be rewritten in the form $a (x - α) (x - β) = 0$
- Note that $(x - α) (x - β) = x^{2} - (α + β) x + α β$
  - It is possible that the roots are repeated, i.e. that $α = β$
- You can then equate the two forms:
  - $a x^{2} + b x + c = a (x - α) (x - β)$
- Then (because $a \neq 0$ ) you can divide both sides of that by a and expand the brackets:
  - $x^{2} + \frac{b}{a} x + \frac{c}{a} = x^{2} - (α + β) x + α β$
- Finally, compare the coefficients
  - $x$ coefficients: $- \frac{b}{a} = (α + β)$
  - Constant terms: $\frac{c}{a} = α β$

Therefore for a quadratic equation $a x^{2} + b x + c = 0$ :
- The sum of the roots $α + β$ is equal to $- \frac{b}{a}$
- The product of the roots $α β$ is equal to $\frac{c}{a}$
You don't need to prove these results on the exam
- But you need to be able to use them to answer questions about quadratics
- They are not on the exam formula sheet
  - So you need to remember (or be able to derive) them
You can use them
- to find the sum and product of the roots if you know the equation
  - Just substitute $a$ , $b$ and $c$ into the formulae
- or to find the equation if you know the sum and product of the roots
  - See the next section

How do I find a quadratic equation from information about its roots?

You may be given the sum and product of an equation's roots and then asked to find the equation
- Usually the equation will need to have integer coefficients
  - For example "A quadratic equation has roots $α$ and $β$ , where $α + β = \frac{7}{2}$ and $α β = - 2$ . Find a quadratic equation with integer coefficients that has roots $α$ and $β$ ."
STEP 1
Start with the formulae linking the roots and coefficients
- $α + β = - \frac{b}{a}$
  - So $\frac{b}{a} = - \frac{7}{2}$
- $α β = \frac{c}{a}$
  - So $\frac{c}{a} = - 2$
STEP 2
Choose a value for $a$ , and find the corresponding values for $b$ and $c$
- Choose a value for $a$ that will multiply to make the values for $α + β$ and $α β$ into integers
  - Let $a = 2$
  - Then $b = - \frac{7}{2} \times 2 = - 7$
  - And $c = - 2 \times 2 = - 4$
STEP 3
Write down the equation using your values for $a$ , $b$ and $c$
- $2 x^{2} - 7 x - 4 = 0$
Note that the answer is not unique
- Any multiple of the equation will also have the same roots
  - e.g. $4 x^{2} - 14 x - 8 = 0$

You may be asked to find a quadratic equation whose roots are related to the roots of another quadratic equation
- I.e. whose roots are expressed in terms of the roots of the first equation
You will often need algebraic tricks to write other expressions with $α$ and $β$ in terms of $α + β$ and $α β$
- $α$ and $β$ are the roots of the first quadratic
- For example:
  - $\begin{array}{rcl} α^{2} + β^{2} & = & α^{2} + 2 α β + β^{2} - 2 α β \\ = & {(α + β)}^{2} - 2 α β \end{array}$
  - $\begin{array}{rcl} α^{3} + β^{3} & = & α^{3} + 3 α β (α + β) + β^{3} - 3 α β (α + β) \\ = & α^{3} + 3 α^{2} β + 3 α β^{2} + β^{3} - 3 α β (α + β) \\ = & {(α + β)}^{3} - 3 α β (α + β) \end{array}$
  - $\begin{array}{rcl} {(α - β)}^{2} & = & α^{2} - 2 α β + β^{2} \\ = & α^{2} + 2 α β + β^{2} - 4 α β \\ = & {(α + β)}^{2} - 4 α β \end{array}$

Then if you know the values of $α + β$ and $α β$ from the first quadratic, you can use them to find the sum or product of the new roots
- For example "A quadratic equation has roots $α$ and $β$ where $α + β = - \frac{3}{2}$ and $α β = 2$ . Form a second quadratic equation with integer coefficients that has roots $\frac{α}{β^{2}}$ and $\frac{β}{α^{2}}$ ."
- The sum of the new roots is $\frac{α}{β^{2}} + \frac{β}{α^{2}} = \frac{α^{3} + β^{3}}{α^{2} β^{2}} = \frac{α^{3} + β^{3}}{{(α β)}^{2}}$
  - We can use the substitution for $α^{3} + β^{3}$ from above
  - So $Sum = \frac{{(α + β)}^{3} - 3 α β (α + β)}{{(α β)}^{2}} = \frac{{(- \frac{3}{2})}^{3} - 3 (2) (- \frac{3}{2})}{{(2)}^{2}} = \frac{45}{32}$
- The product of the new roots is $\frac{α}{β^{2}} \times \frac{β}{α^{2}} = \frac{α β}{α^{2} β^{2}} = \frac{1}{α β}$
  - So $Product = \frac{1}{α β} = \frac{1}{2}$
- With the sum and product we can form the equation as described in the last section
  - $32 x^{2} - 45 x + 16 = 0$

Worked Example

The roots of the quadratic equation $2 x^{2} - 11 x + 5 = 0$ are $α$ and $β$ .

Given that $α > β$ and without solving the equation,

(a) show that $α - β = \frac{9}{2}$

Use $α + β = - \frac{b}{a}$ and $α β = \frac{c}{a}$ to find the sum and product

$α + β = - \frac{(- 11)}{2} = \frac{11}{2}$

$α β = \frac{5}{2}$

Express ${(α - β)}^{2}$ in terms of $α + β$ and $α β$

$\begin{array}{rcl} {(α - β)}^{2} & = & α^{2} - 2 α β + β^{2} \\ = & (α^{2} + 2 α β + β^{2}) - 4 α β \\ = & {(α + β)}^{2} - 4 α β \end{array}$

Substitute to find the value

$\begin{array}{rcl} {(α - β)}^{2} & = & {(\frac{11}{2})}^{2} - 4 (\frac{5}{2}) \\ = & \frac{121}{4} - 10 \\ = & \frac{81}{4} \end{array}$

Take the square root, remembering the $\pm$

$α - β = \pm \frac{9}{2}$

Finally, use the fact that $α > β$

But $α > β$ , therefore $α - β > 0$

$α - β = \frac{9}{2}$

(b) form a quadratic equation, with integer coefficients, which has roots $\frac{α + β}{α}$ and $\frac{α - β}{β}$

Start by finding the sum and product of the new roots

$\begin{array}{rcl} Sum & = & \frac{α + β}{a} + \frac{α - β}{β} \\ = & \frac{β (α + β) + α (α - β)}{α β} \\ = & \frac{α^{2} + β^{2}}{α β} \\ = & \frac{(α^{2} + 2 α β + β^{2}) - 2 α β}{α β} \\ = & \frac{{(α + β)}^{2} - 2 α β}{α β} \\ = & \frac{{(\frac{11}{2})}^{2} - 2 (\frac{5}{2})}{\frac{5}{2}} \\ = & \frac{101}{10} \\ Product & = & \frac{α + β}{a} \times \frac{α - β}{β} \\ = & \frac{(α + β) (α - β)}{α β} \\ = & \frac{(\frac{11}{2}) (\frac{9}{2})}{\frac{5}{2}} \\ = & \frac{99}{10} \end{array}$

Now use $Sum of roots = - \frac{b}{a}$ and $Product of roots = \frac{c}{a}$

$\frac{b}{a} = - \frac{101}{10} and \frac{c}{a} = \frac{99}{10}$

Select $a = 10$ so $b$ and $c$ will have integer values

$a = 10 b = - 101 c = 99$

And finally use those coefficients to write the new equation

$10 x^{2} - 101 x + 99 = 0$

Last updated: 19 October 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Solving Quadratic EquationsNext:Algebraic Division

Roots of Quadratic Equations (Edexcel IGCSE Further Pure Maths)

Revision Note

Discriminants

What is the discriminant of a quadratic function?

How does the discriminant of a quadratic function affect its graph and roots?

How do I solve problems using the discriminant?

Examiner Tips and Tricks

Worked Example

Sum & Product of Roots

How are the roots of a quadratic equation linked to its coefficients?

How do I find a quadratic equation from information about its roots?

Worked Example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Roger B

Author: Dan Finlay

Roots of Quadratic Equations (Edexcel IGCSE Further Pure Maths)

Revision Note

Discriminants

What is the discriminant of a quadratic function?

How does the discriminant of a quadratic function affect its graph and roots?

How do I solve problems using the discriminant?

Sum & Product of Roots

How are the roots of a quadratic equation linked to its coefficients?

How do I find a quadratic equation from information about its roots?

How do I find a quadratic equation with related roots?

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Roger B

Author: Dan Finlay