Solving Inequalities (Edexcel IGCSE Further Pure Maths): Revision Note

Solving Linear Inequalities

What is a linear inequality?

• An inequality tells you that one expression is greater than (“>”) or less than (“<”) another

  • “⩾” means “greater than or equal to”

  • “⩽” means “less than or equal to”

• A linear inequality only has constant terms (numbers with no letters) and terms in x (and/or y)

  • but no x² terms or terms with other powers of x

    • 3x² > 12 is not a linear inequality (it is a quadratic inequality)

How do I solve linear inequalities?

• Solving linear inequalities is just like solving linear equations

  • Follow the same rules, but keep the inequality sign throughout

    • Changing the inequality sign to an equals sign changes the meaning of the problem

• When you multiply or divide both sides by a negative number, you must flip the sign of the inequality 

  • e.g. 1 < 2

    • Multiply both sides by –1 (negative number)

    • It becomes –1 > –2 (sign flips)

• Never multiply or divide by a variable (x)

  • It could be positive or negative

• The safest way to rearrange is simply to add & subtract to move all the terms onto one side

• You also need to know how to

  • use set notation

  • deal with “double” inequalities

How do I represent linear inequalities using set notation?

• We use curly brackets and a colon in set notation

  • $\left\{x:...\right\}$ means "x is in the set such that ..."

    • e.g. the set of all x such that x is greater than 3 is written $\left\{x:x>3\right\}$

• If x  is between two values

  • you can write it as a single set

    • e.g. if x is greater than 3 and less than or equal to 5, then in set notation $\left\{x:3<x\le 5\right\}$

  • or you can write it as separate sets, using the intersection symbol, $\cap$

    • so the above example could also be written in set notation as $\left\{x:x>3\right\}\cap \left\{x:x\le 5\right\}$

  • Either way will get the marks, unless a question specifically asks for one or the other

• If x  is less than one value OR greater than another value (disjoint sets)

  • then the two end values must be written in separate sets using the union symbol, $\cup$

    • e.g. if x is less than 3 or greater than or equal to 5, then in set notation $\left\{x:x<3\right\}\cup \left\{x:\ge 5\right\}$

How do I solve double inequalities?

• Inequalities such as $a<2x<b$ can be solved by doing the same thing to all three parts of the inequality

  • Use the same rules as solving linear inequalities

Solving Quadratic Inequalities

What are quadratic inequalities?

• A quadratic inequality is an inequality with a term in x² (but no higher powers of x)

• Solving the inequality requires solving the corresponding quadratic equation

• Sketching a quadratic graph is essential

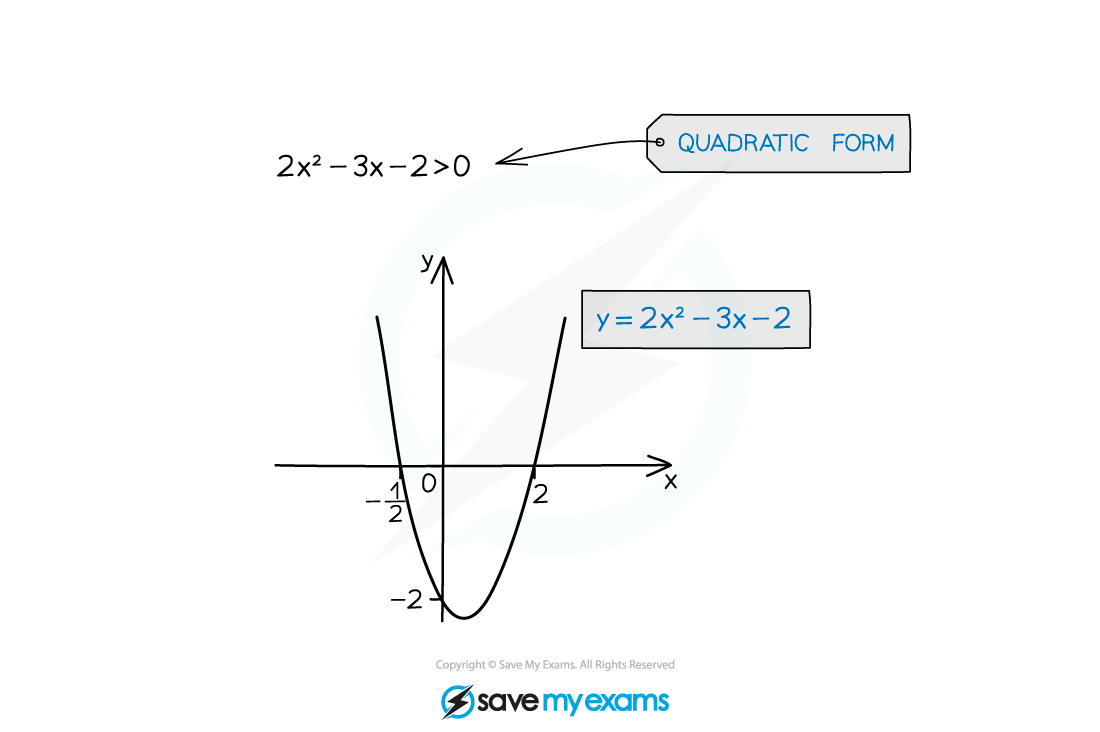
How do I solve quadratic inequalities?

• STEP 1
  Rearrange the inequality into quadratic form with a positive squared term

  • ax² + bx + c > 0  with  a > 0

    • The inequality sign may be >, <, ≤ or ≥

• STEP 2
  Find the roots of the quadratic equation

  • Solve ax² + bx + c = 0 to get x₁ and x₂ where x₁ < x₂

• STEP 3
  Sketch a graph of the quadratic and label the roots

  • As the squared term is positive it will be "U" shaped

• STEP 4
  Identify the region that satisfies the inequality

  • For ax² + bx + c > 0 you want the region above the x-axis

    • The solution is x < x₁ or x > x₂ 

    • It is x ≤ x₁ or x ≥ x₂ if the original inequality was ≥ instead of >

  •  For ax² + bx + c < 0 you want the region below the x-axis

    • The solution is x > x₁ and x < x₂  

    • This is more commonly written as x₁ < x < x₂

    • It is x ≥ x₁ and x ≤ x₂  (x₁ ≤ x ≤ x₂) if the original inequality was ≤ instead of <

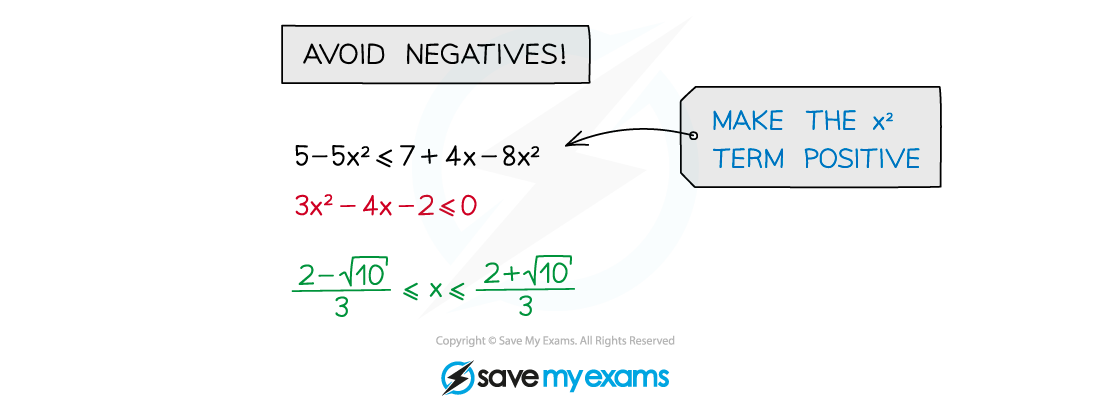
• Avoid multiplying or dividing by a negative number

  • If unavoidable, remember to “flip” the inequality sign (so < → >, ≥ → ≤, etc)

• Avoid multiplying or dividing by a variable (x)

  • The variable could be negative

  • Multiplying or dividing by x² is allowed

    • However this can create extra invalid solutions

• Do rearrange to make the x² term positive