IGCSEFurther MathsEdexcelRevision NotesEquations, Identities & InequalitiesInequalitiesGraphs of Inequalities

Graphs of Inequalities (Edexcel IGCSE Further Pure Maths)

Revision Note

Roger B

Written by: Roger B

Reviewed by: Dan Finlay

Finding Regions using Inequalities

How do I draw inequalities on a graph?

  • STEP 1
    Draw the line (as if using “=”) for each inequality

    • Use a solid line for ≤ or ≥

      • to indicate the line is included

    • Use a dashed line for < or >

      • to indicate the line is not included

  • STEP 2
    Decide which side of line is wanted.

    • Below line if "y ≤ ..." or "y < ..."

    • Above line if "y ≥ ..." or "y > ..."

    • To the left of the line if "x ≤ ..." or "x < ..."

    • To the right of the line if "x ≥ ..." or "x > ..."

    • If unsure, use a point that's not on the line as a test

      • Substitute its x and y value into the inequality and check if the inequality is satisfied

      • This will tell you whether or not the inequality holds true on that side of the line

    • It's helpful to indicate the 'correct side' of each line on your sketch

  • STEP 3
    Choose the region that satisfies all of the inequalities

    • This is the region that is on the correct side of all the lines

    • The exam question will often ask you to shade and/or label the region

Examiner Tips and Tricks

  • You can also indicate a region by shading the unwanted bits and leaving the region unshaded

    • Some students find this easier

    • The mark scheme awards full marks for either method

Worked Example

On the axes given below show, by shading on your sketch, the region that satisfies the following three inequalities:

3 x plus 2 y greater or equal than 12                  y less than 2 x                 x less than 3

Label the region R.


First draw the three straight lines, 3 x plus 2 y equals 12, y equals 2 x and x equals 3
You may wish to rearrange 3 x plus 2 y equals 12 to the form y equals m x plus c first:

table row cell 2 y end cell equals cell negative 3 x plus 12 end cell row y equals cell negative 3 over 2 x plus 6 end cell end table

The line 3 x plus 2 y greater or equal than 12 takes a solid line because of the "≥"
The lines y less than 2 x and x less than 3 take dotted lines because of the "<"

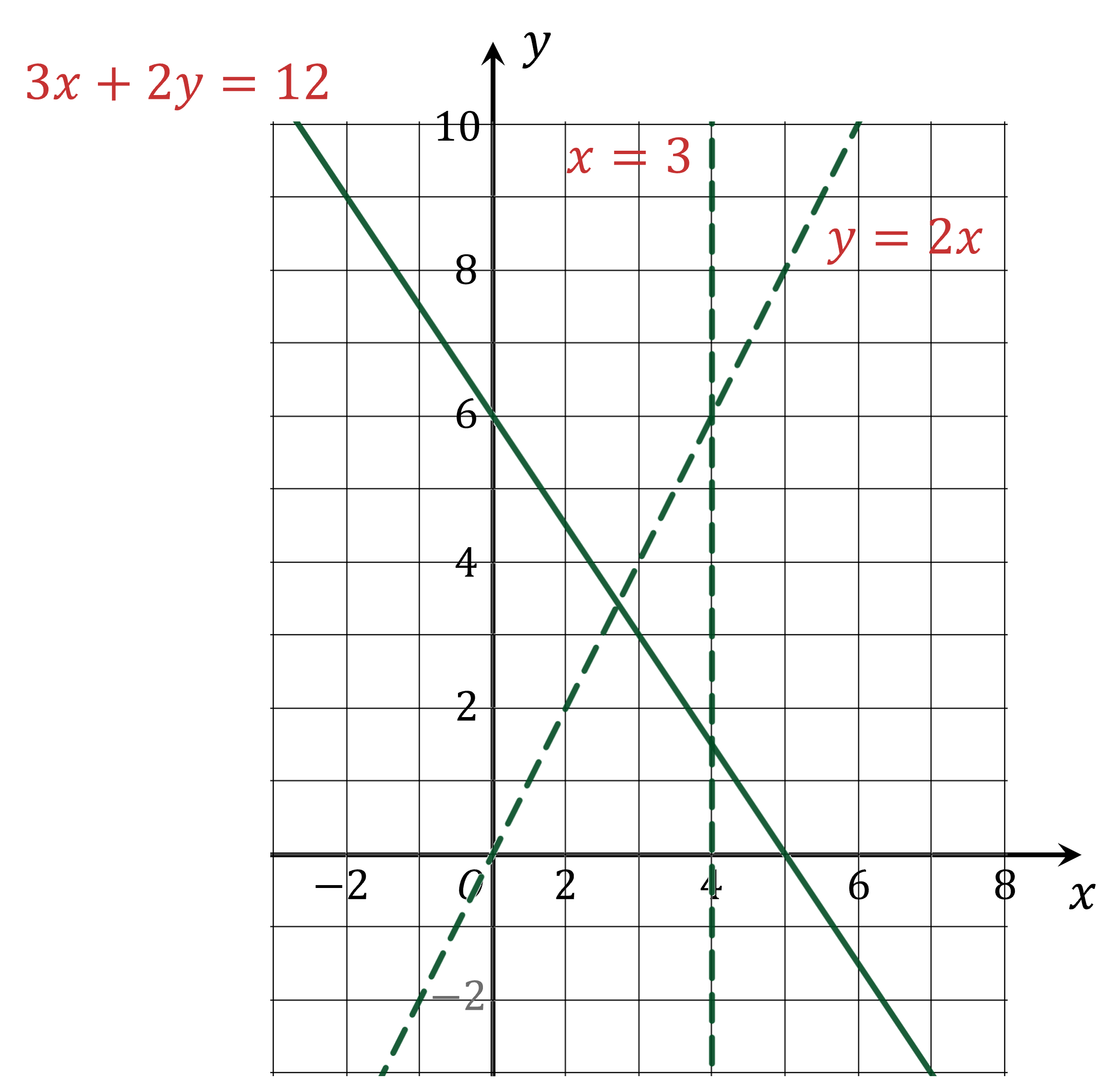
Graph of lines from question

Now we need to determine the wanted and unwanted regions

For 3 x plus 2 y greater or equal than 12 (or y greater or equal than negative 3 over 2 x plus 6), the wanted region is above the line
We can check this with the point (0, 0)

3 open parentheses 0 close parentheses plus 2 open parentheses 0 close parentheses greater or equal than 12 is false, so (0, 0) does not lie in the wanted region for table attributes columnalign right center left columnspacing 0px end attributes row cell 3 x plus 2 y end cell greater or equal than 12 end table

For y less than 2 x, the wanted region is below the line
If unsure, check with another point, for example (1, 0)

0 less than 2 open parentheses 1 close parentheses is true, so (1, 0) lies in the wanted region for table row y less than cell 2 x end cell end table

For x less than 3, the wanted region is to the left of x equals 3 
(If unsure, you could check with a point)

Finally, shade the region that satisfies all three inequalities on the graph
Don't forget to label the region R

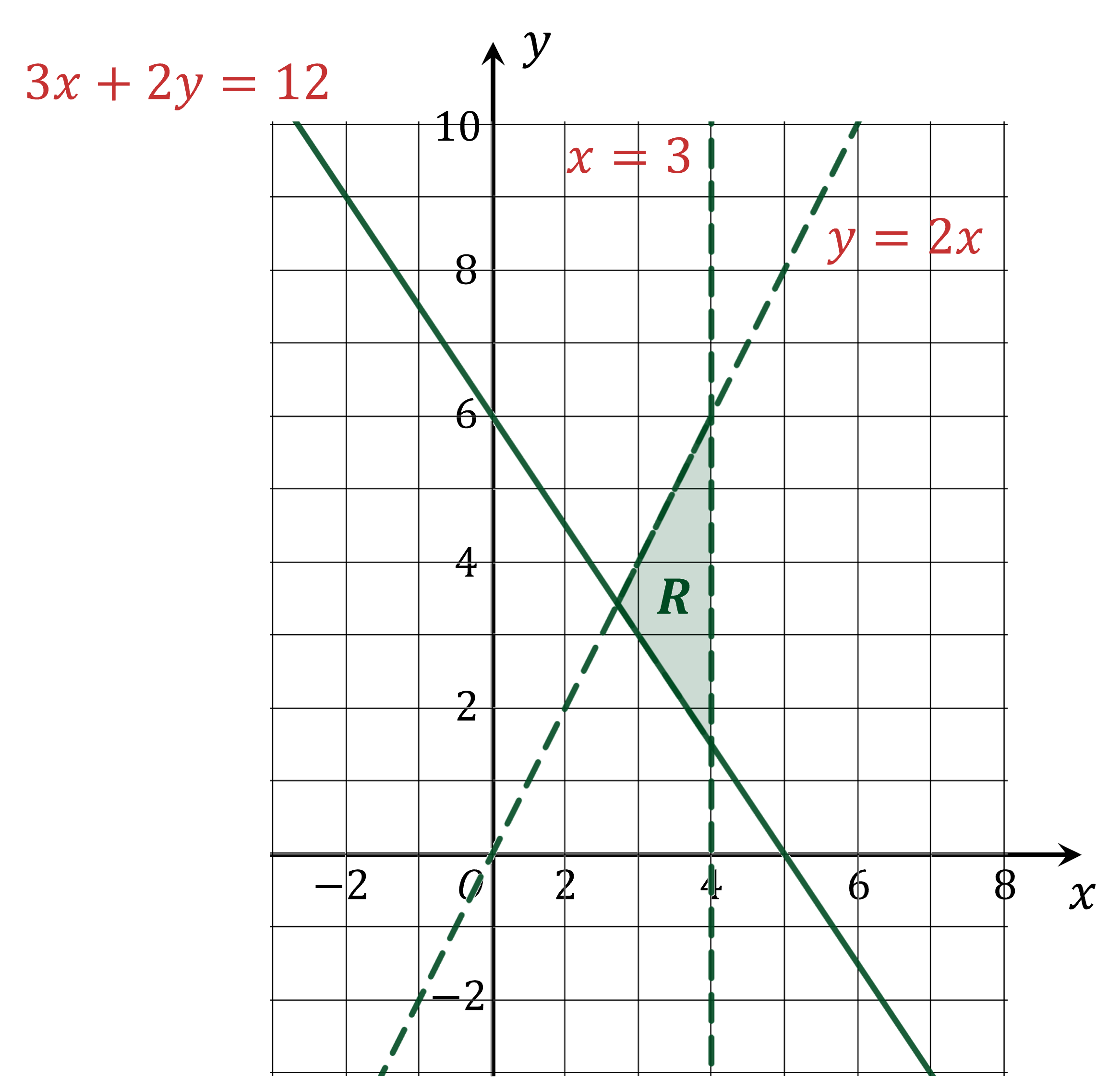
Graph of region defined by inequalities

Interpreting Graphical Inequalities

How do I determine the inequalities if given a region on a graph?

  • STEP 1
    Write down the equation of each line on the graph

  • STEP 2
    Remember that lines are drawn with:

    • A solid line for ≤ or ≥ (to indicate line included in region)

    • A dashed line for < or > (to indicate line not included)

  • STEP 3
    Replace = sign with:

    • ≤ or < if shading below line

    • ≥ or > if shading above line

      • Use a point to test if not sure

How do I find optimal solutions from a region on an inequalities graph?

  • A question may ask you to optimise a function for points in the region

    • For example, "For all points in the region with coordinates open parentheses x comma space y close parentheses,  P equals 3 x minus 2 y. Find the greatest value of P."

  • In these questions the inequalities will usually all be ≤ or ≥

    • This means all the points on the lines are included in the region

  • The optimal solution (minimum or maximum) will always occur at a point where two lines intersect

    • Substitute the coordinates of the intersection points into the function

    • Choose the point which gives the maximum or minimum value, as required

    • If the question asks for integer solutions

      • Check that the optimal intersection point coordinates are both integers

      • If they are not, the solution will occur at the point with integer coordinates nearest the optimal intersection

Worked Example

(a) Write down the three inequalities that define the shaded region in the diagram below.

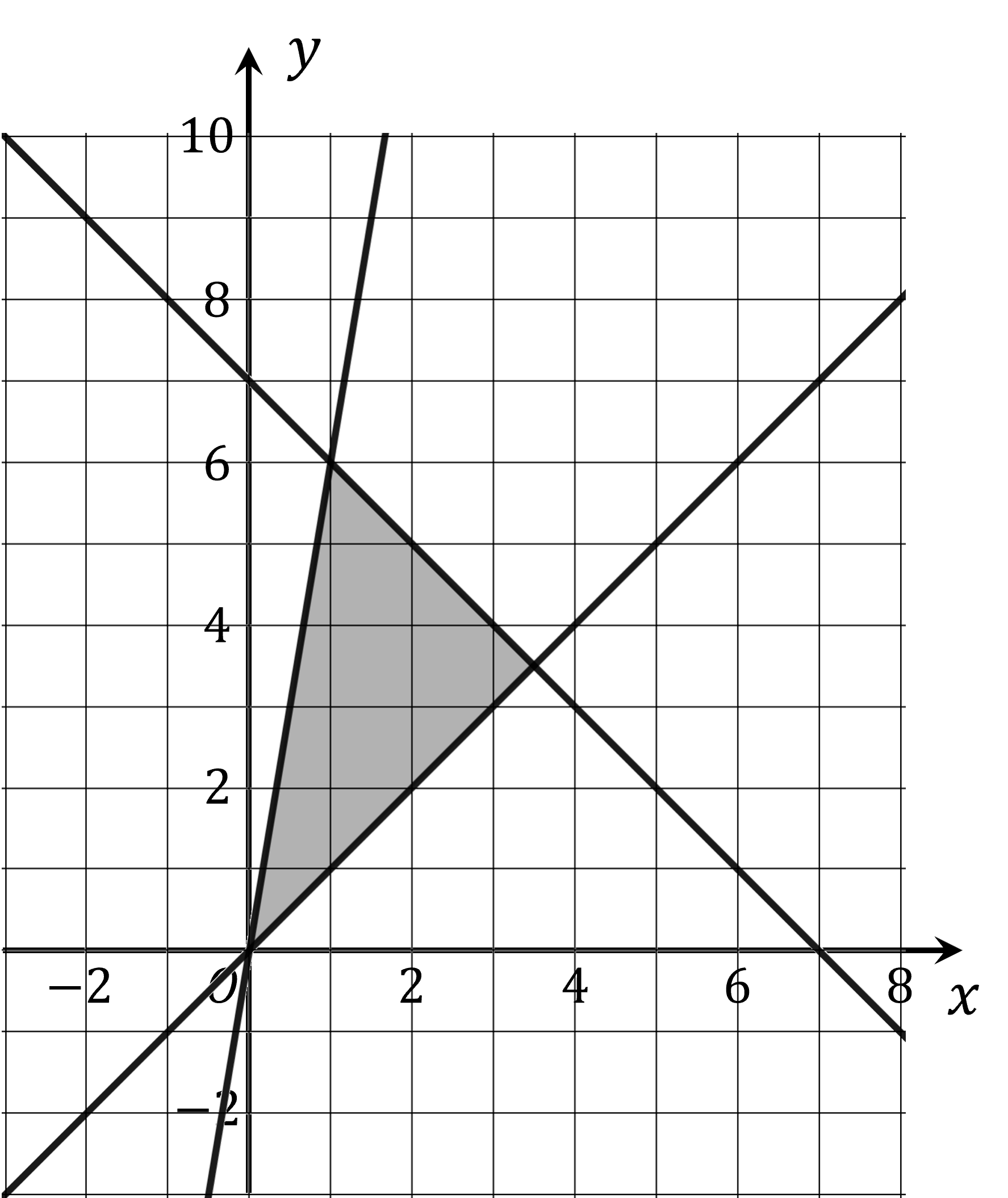
Graph of region defined by inequalities

Start by determining the equations of the three lines on the graph.

The line through points (0, 0) and (1, 6) has equation  y equals 6 x
The line through points (0, 0) and (2, 2) has equation  y equals x
The line through points (0, 7) and (7, 0) has equation  y equals negative x plus 7

Label the lines on the diagram with these equations

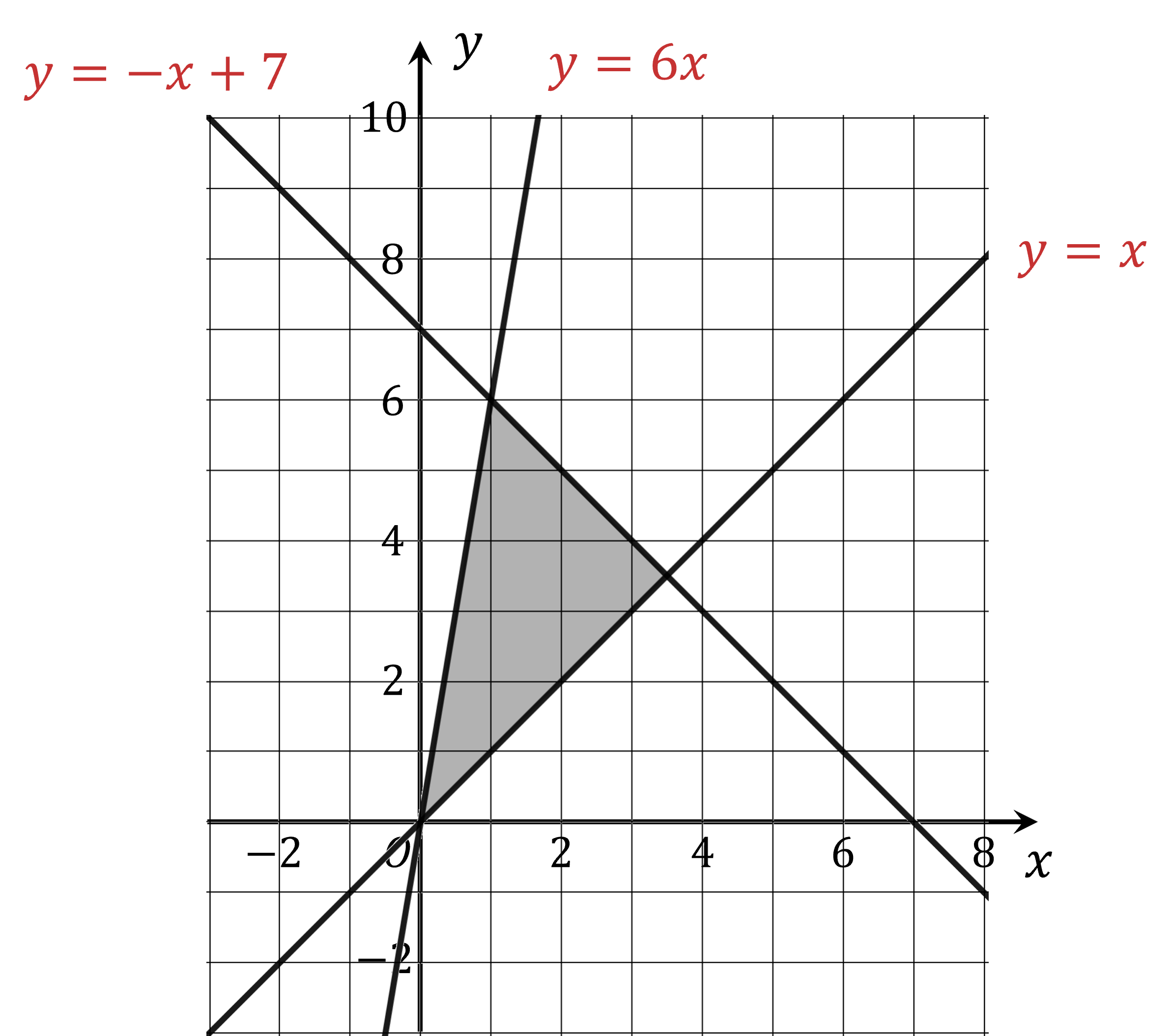
Graph with equations of lines added on


The lines are solid, so all the inequalities will be less or equal than or greater or equal than

The region is below the lines  y equals negative x plus 7  and  y equals 6 x, so those will be less or equal than
The region is above the line  y equals x, so that will be greater or equal than

Write down these inequalities for the final answer

bold italic y bold less or equal than bold minus bold italic x bold plus bold 7 bold comma bold space bold space bold italic y bold less or equal than bold 6 bold italic x  and  bold italic y bold greater or equal than bold italic x   

For all points in the shaded region, with coordinates open parentheses x comma space y close parentheses,  P equals 20 x minus 3 y.

(b) Find the greatest value of P.

The greatest (and least) values of P will occur at one of the intersections of the lines bordering the region

(These points can be seen on the graph, but it would be worth substituting the coordinates into the equations to make sure)


So we need to find the value of P at each of those points

For point (0, 0):  P equals 20 open parentheses 0 close parentheses minus 3 open parentheses 0 close parentheses equals 0

For point (1, 6):  P equals 20 open parentheses 1 close parentheses minus 3 open parentheses 6 close parentheses equals 2

For point (3.5, 3.5):  P equals 20 open parentheses 3.5 close parentheses minus 3 open parentheses 3.5 close parentheses equals 59.5

The greatest value is bold italic P bold equals bold 59 bold. bold 5

Last updated:

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Did this page help you?

    Previous:Solving InequalitiesNext:Basic Coordinate Geometry
    Author
    Reviewer
    Roger B

    Author: Roger B

    Expertise: Maths

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.