Algebraic Division (Edexcel IGCSE Further Pure Maths)
Revision Note
Written by: Roger B
Reviewed by: Dan Finlay
Algebraic Division
What is algebraic division?
Algebraic division (or polynomial division) is a method for splitting polynomials into factor pairs (with or without an accompanying remainder term)
On the exam you will use it to factorise polynomials, or to help simplify algebraic fractions
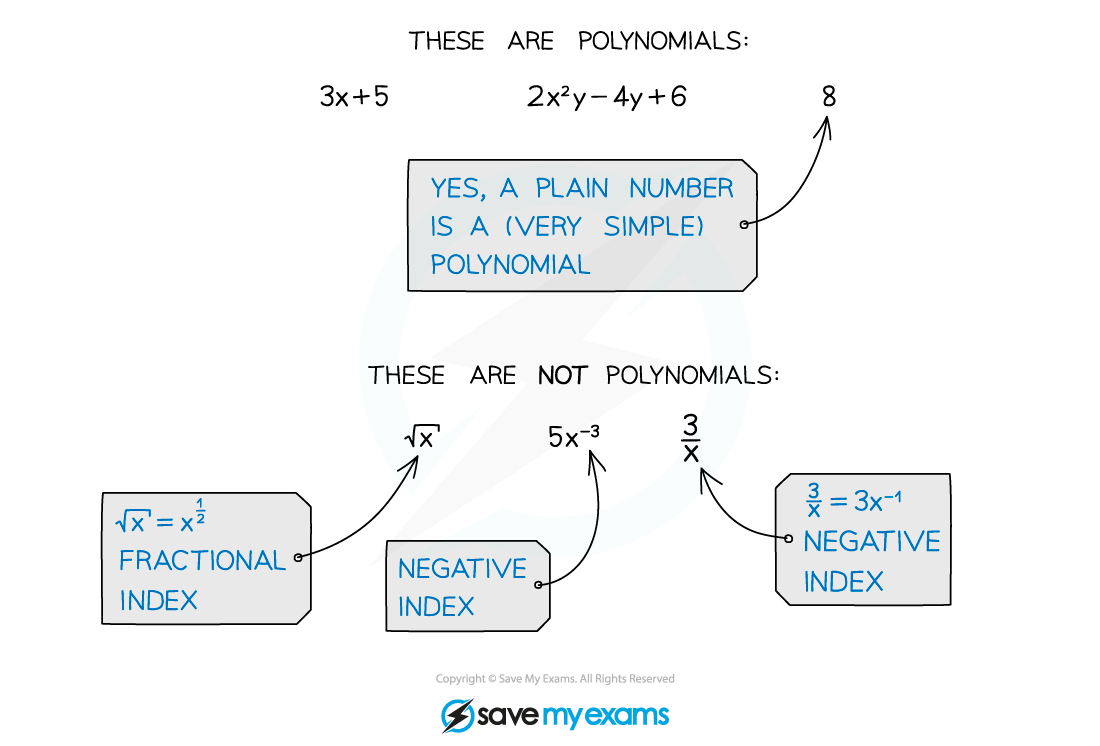
Remember that a polynomial is an algebraic expression consisting of
a finite number of terms
with non-negative integer indices only
How do I perform algebraic division?
The method used for algebraic division is just like the method used to divide regular numbers
i.e. the long division method (sometimes called 'bus stop division')
On your exam the polynomial you are dividing (known as the dividend) will normally be of degree 3 or 4
That is, with powers of x up to x3 or x4
The term you are dividing by (known as the divisor) will be a linear term
Usually in the form (x ± a)
But possibly in the form (ax ± b)
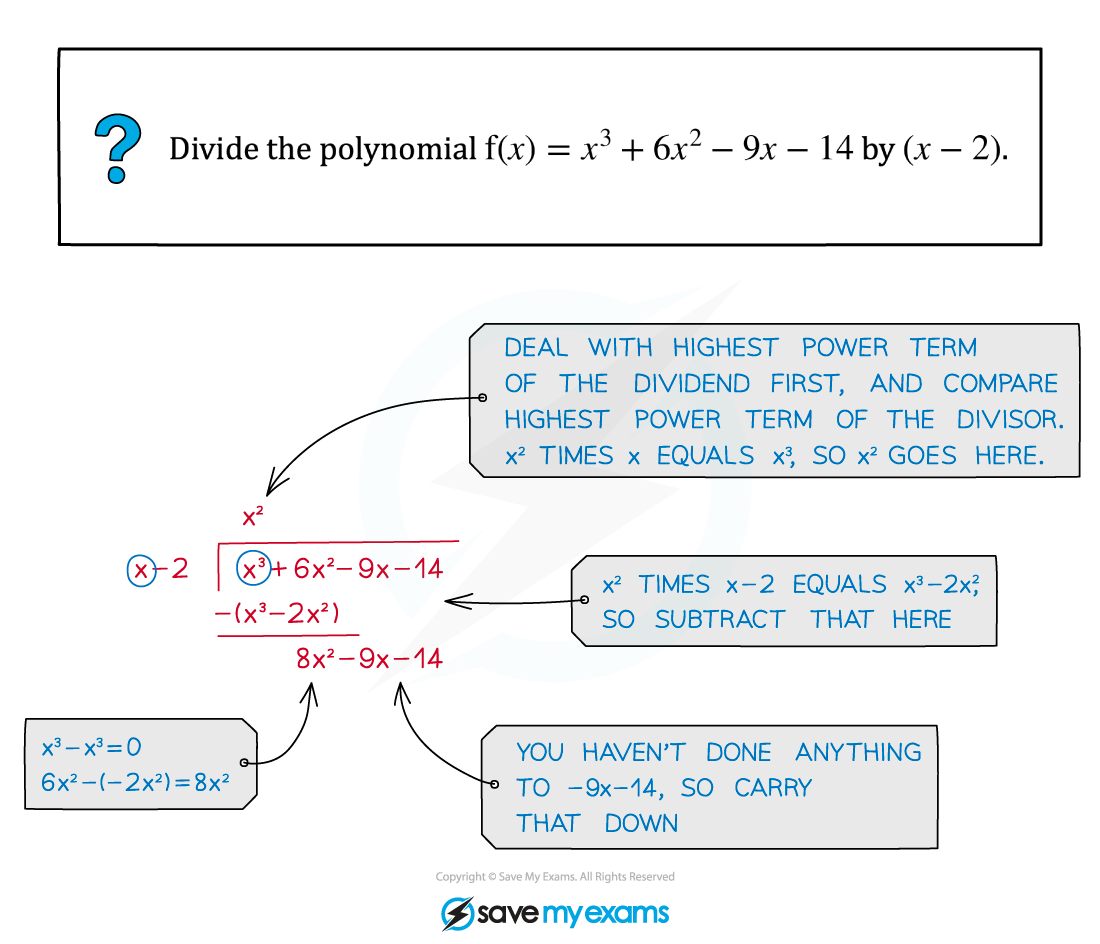
The answer to an algebraic division question is built up term by term
Working downwards in powers of the variable (usually x)
Start with the highest power term of the answer
Write out this multiplied by the divisor and subtract
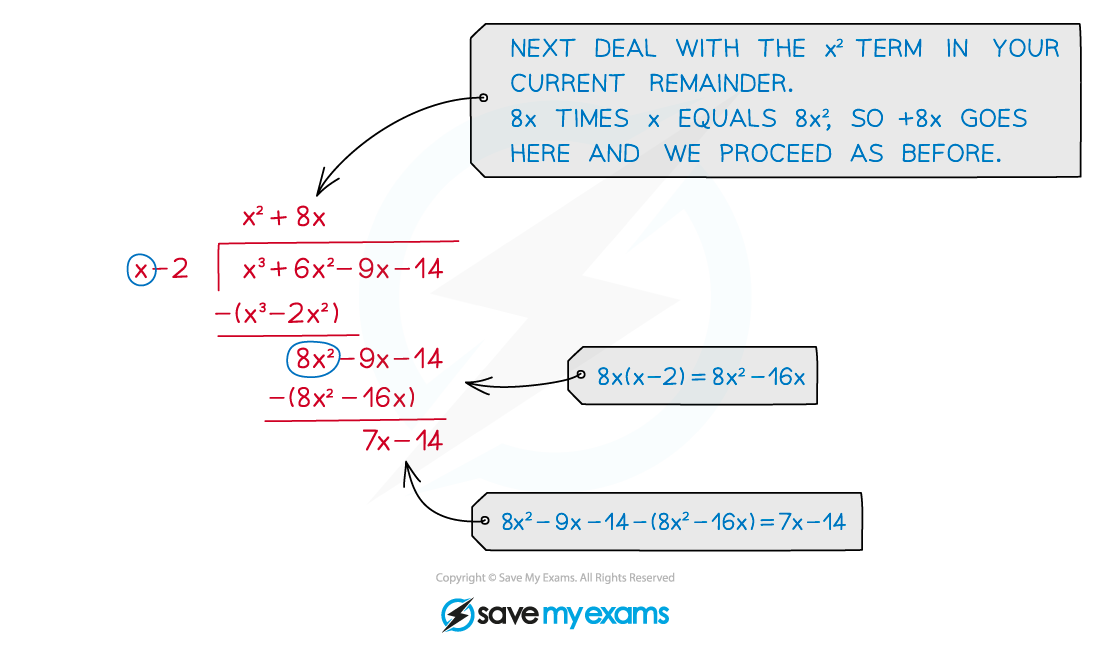
Continue the process for each decreasing power term
multiplying by the divisor and subtracting each time
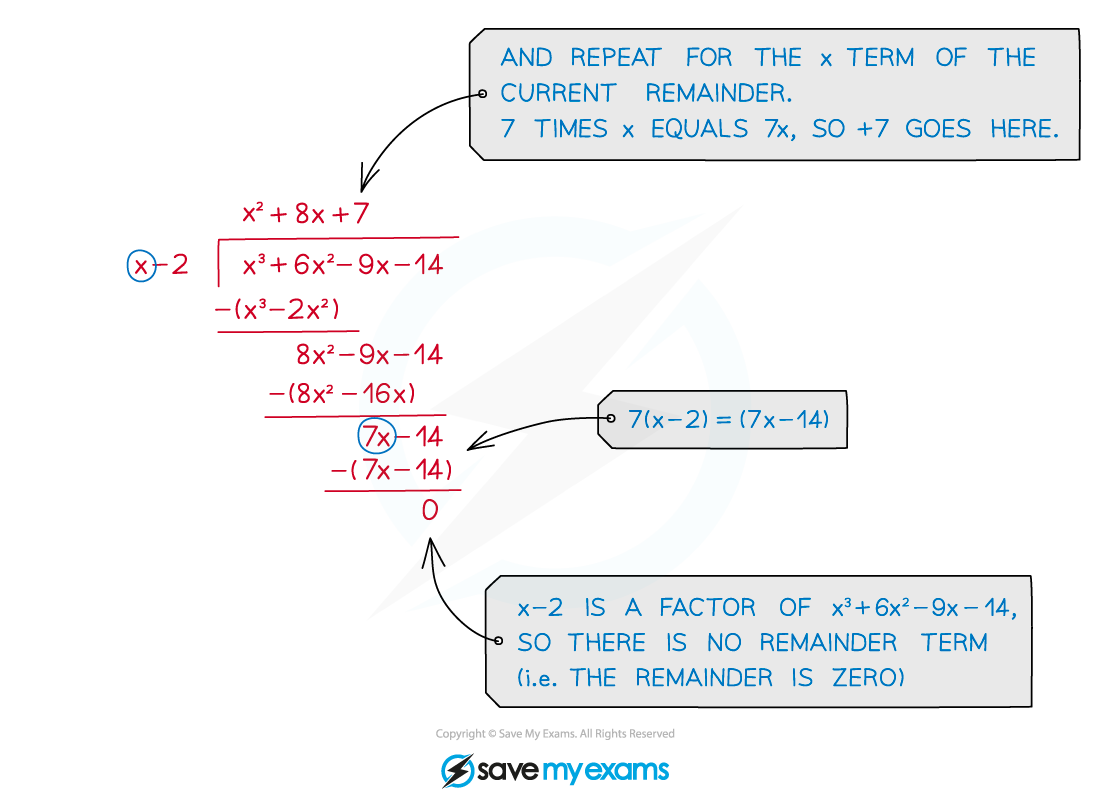
Continue until you are left only with a number (with no x's)
That number is the remainder
If the divisor is a factor of the polynomial, the remainder will be zero
Examiner Tips and Tricks
Don't rush when doing algebraic division
Finding and fixing a mistake can take longer than taking the time to do it right the first time!
Before starting algebraic division make sure it is really necessary
For example, if all you need is the remainder then using the remainder theorem would be quicker
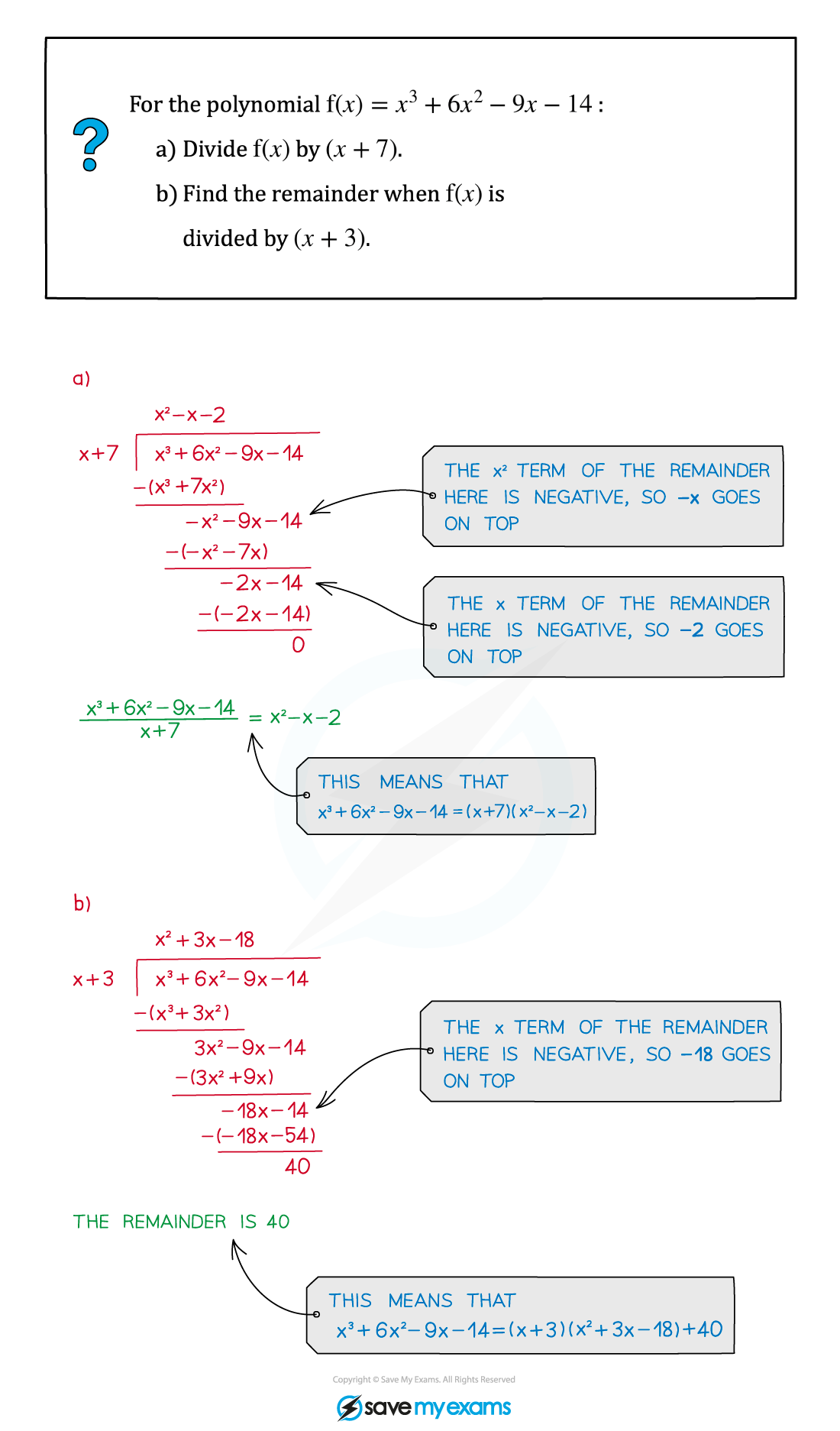
Worked Example
Last updated:
You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
