Graphs of Rational Functions (Edexcel IGCSE Further Pure Maths)

Revision Note

Written by: Dan Finlay

Reviewed by: Lucy Kirkham

Linear Rational Functions & Graphs

What is a linear rational function?

A (linear) rational function is of the form $f (x) = \frac{a x + b}{c x + d}, x \neq - \frac{d}{c}$
Its domain is the set of all real values except $- \frac{d}{c}$
- Because $x = - \frac{d}{c}$ would make the denominator zero
Its range is the set of all real values except $\frac{a}{c}$
- Because there's no value of $x$ for which $\frac{a x + b}{c x + d} = \frac{a}{c}$
The reciprocal function $f (x) = \frac{1}{x}$ is a special case of a rational function

What are the key features of linear rational graphs?

The graph has a y-intercept at $(0, \frac{b}{d})$ provided $d \neq 0$
- The is found by substituting $x = 0$
The graph has one x-intercept at $(- \frac{b}{a}, 0)$ provided $a \neq 0$
- This is found by setting the numerator equal to zero and solving the equation
The graph has two asymptotes
- A horizontal asymptote: $y = \frac{a}{c}$
  - This is the limiting value when the value of x gets very large in the positive or negative direction
- A vertical asymptote: $x = - \frac{d}{c}$
  - This is the value that causes the denominator to be zero
The graph does not have any minimum or maximum points
If you are asked to sketch or draw a rational graph:
- Give the coordinates of any intercepts with the axes
- Give the equations of the asymptotes

Examiner Tips and Tricks

A horizontal line should only intersect this type of graph once at most
The only horizontal line that should not intersect the graph is the horizontal asymptote
- This can be used to check your sketch in an exam

Worked Example

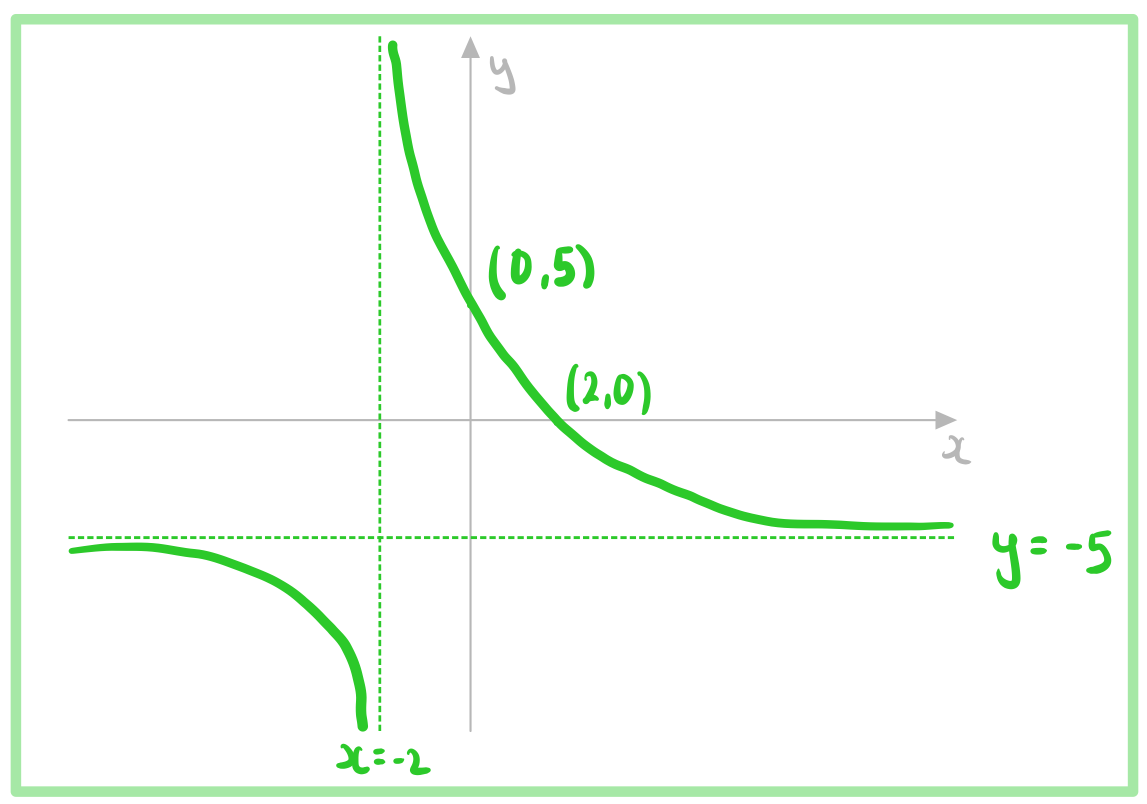
The function $f$ is defined by $f (x) = \frac{10 - 5 x}{x + 2}$ for $x \neq - 2$ .

(a) Write down the equations of the horizontal and vertical asymptotes of the graph of $y = f (x)$ .

The horizontal asymptote is the limiting value as x becomes very large in the positive or negative direction

When that happens, the '10' in the numerator and '2' in the denominator no longer affect the value of the function much

For large values of $x$

$f (x) \approx \frac{- 5 x}{x} = - 5$

That means the horizontal asymptote will be at $y = - 5$

Horizontal asymptote: $y = - 5$

The vertical asymptote occurs where the denominator becomes zero

$\begin{array}{rcl} x + 2 & = & 0 \\ x & = & - 2 \end{array}$

Vertical asymptote: $x = - 2$

(b) Find the coordinates of the intercepts of the graph of $y = f (x)$ with the coordinate axes.

The y-intercept occurs when $x = 0$

$f (0) = \frac{10 - 5 (0)}{(0) + 2} = \frac{10}{2} = 5$

y-intercept: $(0, 5)$

The x-intercept occurs when $y = f (x) = 0$

$\begin{array}{rcl} \frac{10 - 5 x}{x + 2} & = & 0 \\ 10 - 5 x & = & 0 \\ 5 x & = & 10 \\ x & = & 2 \end{array}$

x-intercept: $(2, 0)$

Don't forget to include (and label) the asymptotes, and to label the axis intercepts

Last updated: 20 October 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Graphs of PolynomialsNext:Solving Equations Graphically