IGCSEFurther MathsEdexcelRevision NotesCoordinate Geometry & GraphsGraphsGraphing Functions

Graphing Functions (Edexcel IGCSE Further Pure Maths): Revision Note

Exam code: 4PM1

Written by: Roger B

Reviewed by: Dan Finlay

Updated on 20 October 2024

Graphing Functions

How do I graph the function y = f(x)?

A point $(a, b)$ lies on the graph of $y = f (x)$ if $f (a) = b$
The horizontal axis is used for the domain
- these are the x-values
The vertical axis is used for the range
- these are the corresponding y-values
Graphing a function can involve any or all of the following skills
- creating a table of values
- knowing the general shapes and characteristics of different types of graphs
- finding axis intercepts
- finding turning points (including maxima and minima)
- identifying asymptotes

What is the difference between “draw” and “sketch”?

'Sketch' questions will not provide a detailed grid to draw the graph on
- A sketch is meant to show key features of a graph
  - It does not need to be perfectly to scale
  - It does not need to plot points precisely
- When asked to sketch you should:
  - Show the correct general shape
  - Label any key points such as the intersections with the axes
  - Label the axes
  - Label the graph by giving its function or equation
'Draw' questions will always provide a detailed grid to draw the graph on
- A drawing of a graph is meant to be as accurate as possible
- When asked to draw you should:
  - Use a ruler for any straight lines
  - Draw to scale
  - Plot any points precisely
  - Join points with a straight line or smooth curve
  - Label any key points such as the intersections with the axes
  - Label the axes
  - Label the graph by giving its function or equation

Can my calculator help me sketch/draw a graph?

Your calculator may be able to display graphs of functions
- If so make sure you are familiar with how this feature works
This can be useful for checking your work
It can also help with identifying
- the general shape of a graph
- axis intercepts
- turning points (including maxima and minima)
But be careful, especially on 'show that' questions
- Make sure key parts of an answer are backed up by working
- Marks may depend on this

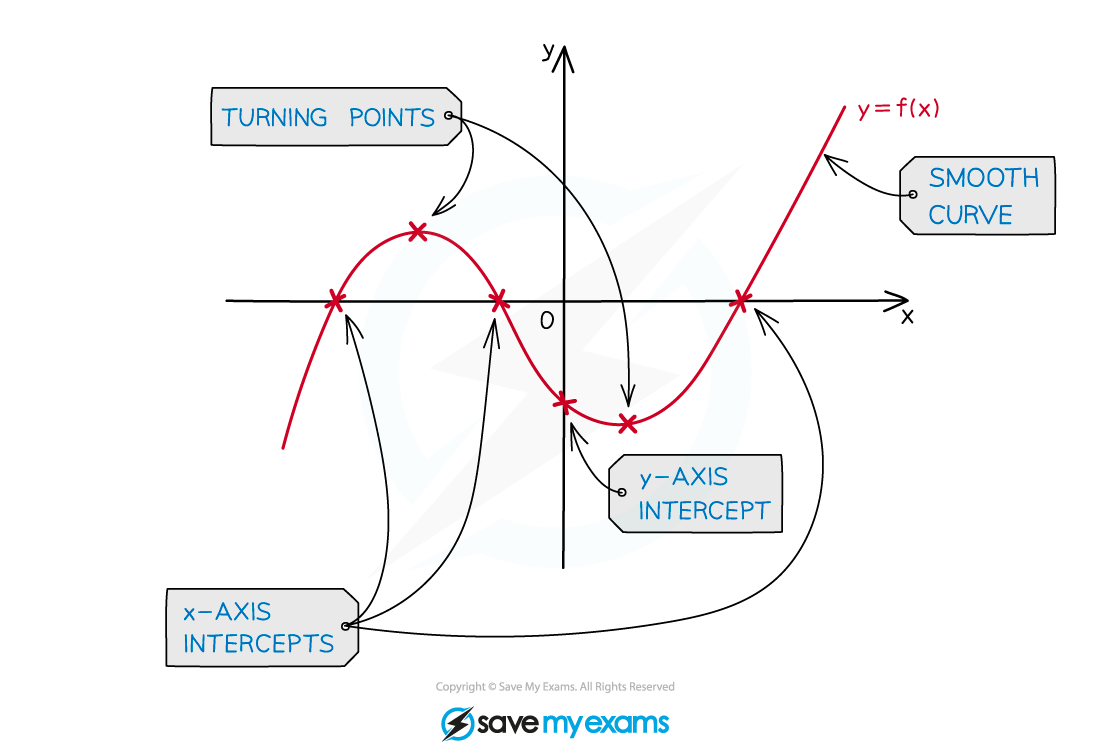
Key Features of Graphs

What are the key features of graphs?

You should be familiar with the following key features and know how to identify them

Local minima and maxima
- These are points where the graph has a minimum/maximum for a local region
  - They are the 'peaks' or 'valleys' of a graph
  - They are not necessarily the minimum or maximum for the whole graph
- They are also called turning points
- A graph can have multiple local minima or maxima
- They occur where the gradient of the graph is equal to zero
  - So if you are graphing $y = f (x)$
  - Turning points will occur where $f^{'} (x) = 0$
Intercepts
- y-intercepts are where the graph crosses the y-axis
  - At these points $x = 0$
- x-intercepts are where the graph crosses the x-axis
  - At these points y = 0
  - These points are also called the roots of the function
Symmetry
- Some graphs have lines of symmetry
  - E.g. a quadratic graph has a vertical line of symmetry through its minimum or maximum point
Asymptotes
- These are lines which the graph will get closer to but not cross
- These can be horizontal or vertical
  - Exponential graphs have horizontal asymptotes
  - Logarithmic graphs and graphs of rational functions have vertical asymptotes

Examiner Tips and Tricks

Don't forget to label the graph, the axes and key features when drawing or sketching a graph
- Marks may depend on this
Your calculator may be able to help you with drawing or sketching a graph
- But don't forget to show working, especially in a 'show that' question
Sketching a graph can often be useful even if a question doesn't require it

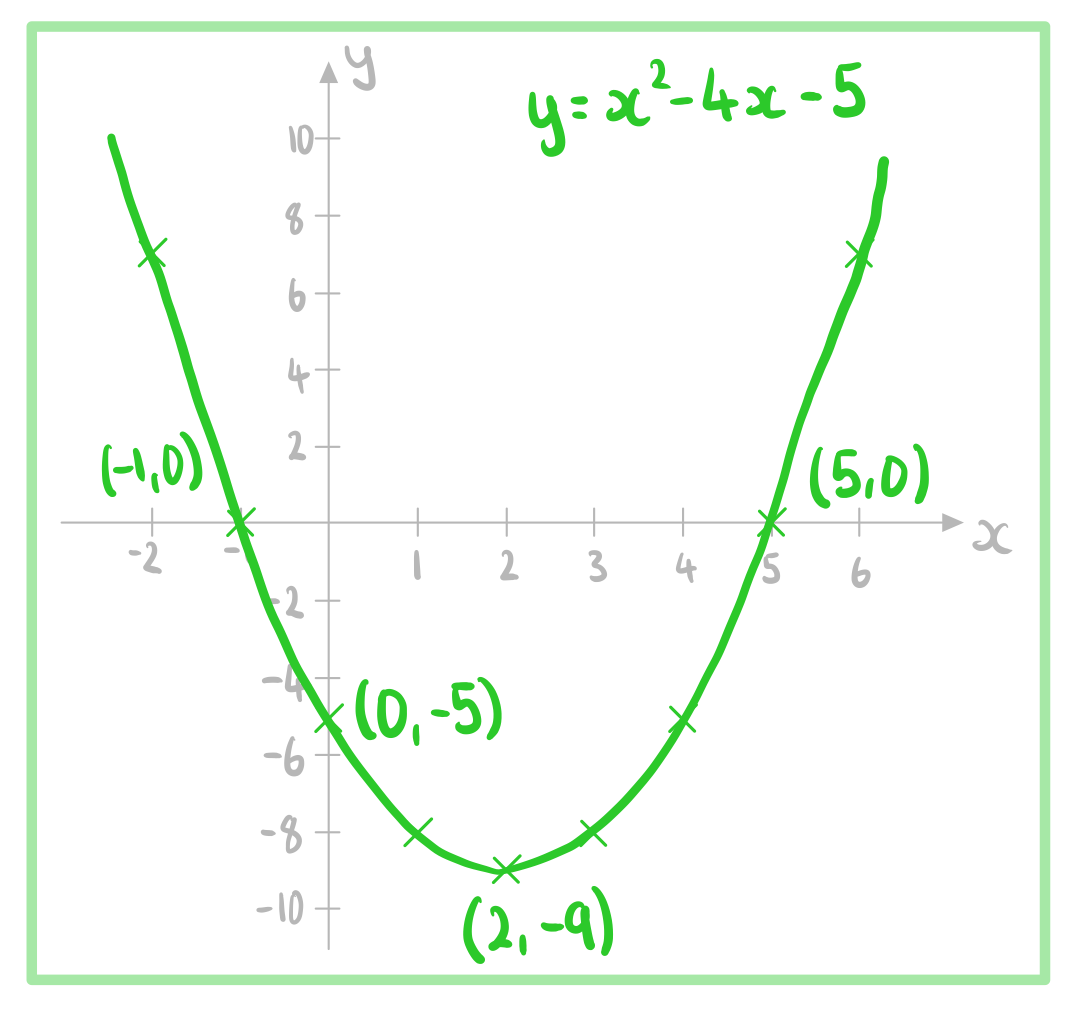
Worked Example

A function is defined by $f (x) = x^{2} - 4 x - 5$ .

Sketch the graph $y = f (x)$ .

Remember, 'sketch' here means we only need to show the general shape and key features

This is a positive quadratic, so it is going to be a 'u-shaped' parabola

Find the y-intercept by substituting in $x = 0$

$f (0) = {(0)}^{2} - 4 (0) - 5 = - 5$

So the y-intercept is $(0, - 5)$

The x-intercepts will occur when $y = f (x) = 0$

$\begin{array}{rcl} x^{2} - 4 x - 5 & = & 0 \\ (x - 5) (x + 1) & = & 0 \end{array}$

$x = 5, x = - 1$

So the x-intercepts are $(5, 0)$ and $(- 1, 0)$

The turning point will occur when $f^{'} (x) = 0$

$f^{'} (x) = 2 x - 4$

$\begin{array}{rcl} 2 x - 4 & = & 0 \\ 2 x & = & 4 \\ x & = & 2 \end{array}$

Substitute into $f (x)$ to find the corresponding y-value

$\begin{array}{rcl} f (2) & = & {(2)}^{2} - 4 (2) - 5 \\ = & 4 - 8 - 5 \\ = & - 9 \end{array}$

So the turning point is $(2, - 9)$

Sketch a graph showing the correct general shape and incorporating all the key points identified above
Label the graph, the axes, and the key features

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

Beth
IGCSE Student

This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

Fathima
A Level Student

Incredible! SO worth my money, the revision notes have everything I need to know and are so easy to understand. I actually enjoy revising! It makes me feel a lot more confident for my GCSEs in a few months.

Kate
GCSE Student

Absolutely brilliant, both my girls used it for A levels and GCSE. It's saves on paper copies, also beneficial exam questions ranked from easy to hard. It's removed a lot of stress from the exams.

Sameera
Parent

Just to say that your resources are the best I have seen and I have been teaching chemistry at different levels for about 40 years

Mark
Chemistry Teacher

Excellent