Basic Coordinate Geometry (Edexcel IGCSE Further Pure Maths)

Basic Coordinate Geometry

What are Cartesian coordinates?

• Cartesian coordinates are the coordinates used in the x-y coordinate system

  • They allow us to label where things are in a two-dimensional plane

• In the 2D Cartesian system, the horizontal axis is labelled x  and the vertical axis is labelled y

   

What can I do with coordinates?

• If you have two points with coordinates and then you should be able to find

  • The distance between the two points

  • The point that divides the line between the two points in a given ratio

  • The gradient of the line joining the two points

How do I find the distance between two points?

• The distance  between two points with coordinates and can be found using the formula

  • 

• is the hypotenuse of a right-angled triangle

  • The differences between the -coordinates and the -coordinates give the other two side lengths

  • So by Pythagoras’ Theorem  

How do I divide the line between two points in a given ratio?

• The coordinates of the point dividing the line joining  and  in the ratio  are given by

  • 

• If  then the point is closer to 

• If then the point is closer to 
  

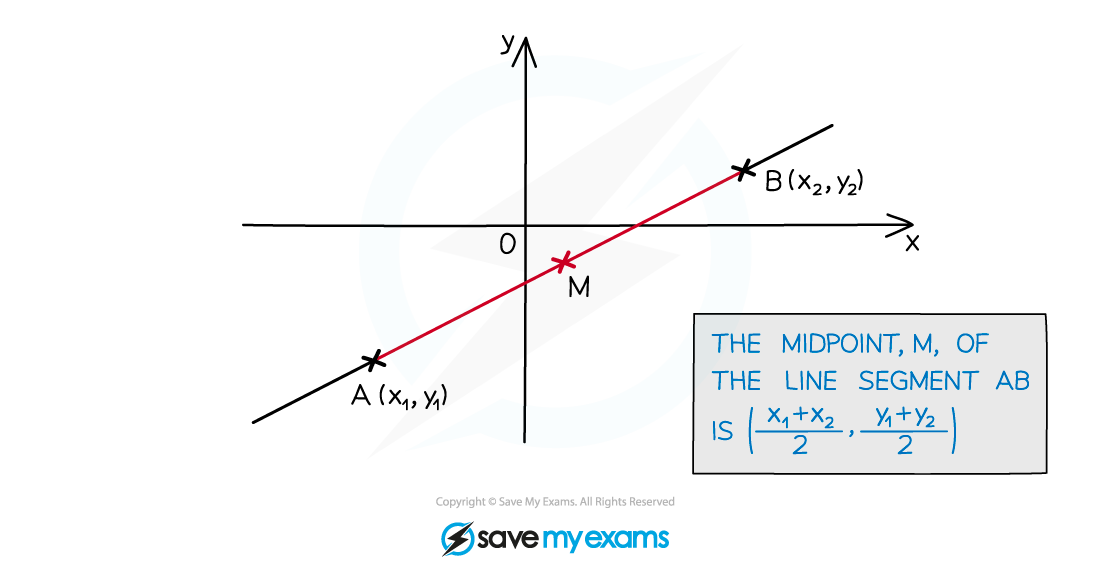
How do I find the midpoint between two points?

• The midpoint is the point halfway between the two points

  • This is just 'dividing in a given ratio' where the ratio is

• The coordinates of the midpoint will be

  • 

How do I find the gradient of a straight line joining two points?

• The gradient of a line between two points with coordinates and can be found using the formula

  • 

• This is also known as