Introduction to Derivatives (Edexcel IGCSE Further Pure Maths)

Introduction to Derivatives

What is differentiation?

• Differentiation is part of the branch of mathematics called calculus

• It is concerned with the rate at which changes takes place

  • So it has many real‑world applications:

    • The rate at which a car is moving (its speed)

    • The rate at which a virus spreads amongst a population

• To begin to understand differentiation you’ll need to understand gradients

How are gradients related to rates of change?

• Gradient in everyday language refers to steepness.

  • For example, the gradient of a road up the side of a hill is important to lorry drivers

• On a graph the gradient refers to how 'steep' a line or a curve is

• It is a way of measuring how fast y  changes as x  changes

  • This may be referred to as the 'rate of change of y  with respect to x'

• So gradient describes the rate at which change happens

How do I find the gradient of a curve using its graph?

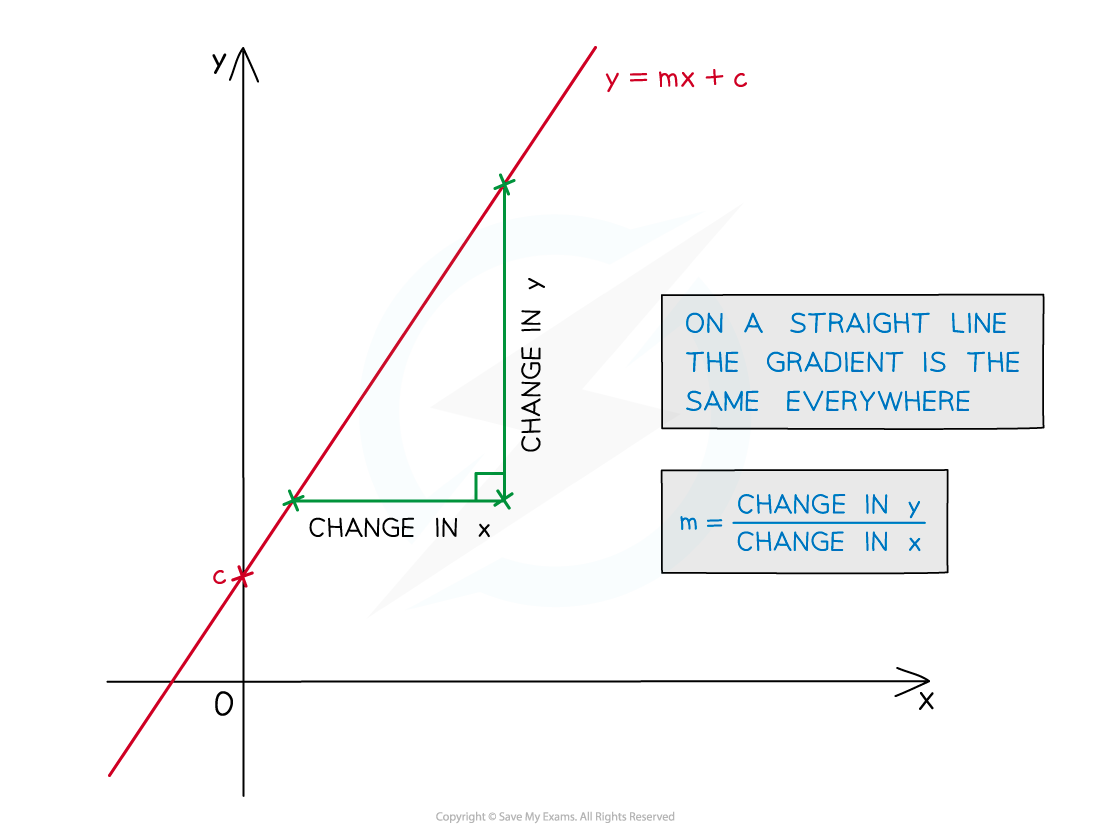
For a straight line the gradient is always the same (constant)

• Recall  y = mx + c, where m  is the gradient

• For a curve the gradient changes as the value of x  changes

  • A tangent is a straight line that touches the curve at one point

    • At any point on the curve, the gradient of the curve is equal to the gradient of the tangent at that point

How do I find the gradient of a curve using calculus? 

• The equation of a curve can be given in the form

  • Substituting x-coordinate inputs gives y-coordinate outputs

• It is possible to create an algebraic function that take inputs of x-coordinates

  • and gives outputs that are gradients

    • No graph sketching required!

• This type of function has a few commonly used names:
  

  • The gradient function

  • The derivative

  • The derived function

• The way to write this function is 

  • This is pronounced "dy by dx" or "dy over dx"

  • In function notation, it can be written 

    • pronounced "f-dash-of-x" or "f-prime-of-x"

• To get from  to  you need to do an operation called differentiation

  • Differentiation turns curve equations into gradient functions

  • There are standard formulae used to differentiate all the basic functions

    • See the 'Differentiating Basic Functions' revision note

  • There are also various methods for differentiating more complicated functions

    • See the 'Techniques of Differentiation' revision note

• Once you know  for a curve, you can find the gradient for any point on the curve

  • gives the value of the gradient when 

    • See the 'Finding Gradients' revision note for more details