Volumes of Revolution (Edexcel IGCSE Further Pure Maths)

Revision Note

Written by: Roger B

Reviewed by: Dan Finlay

Volumes of Revolution About the x-axis

What is a volume of revolution about the x-axis?

A solid of revolution is formed
- when an area bounded by a function $y = f (x)$ and the lines $x = a$ and $x = b$
- is rotated $2 π$ radians $(360 °)$ about the $x$ -axis
The volume of revolution is the volume of this solid

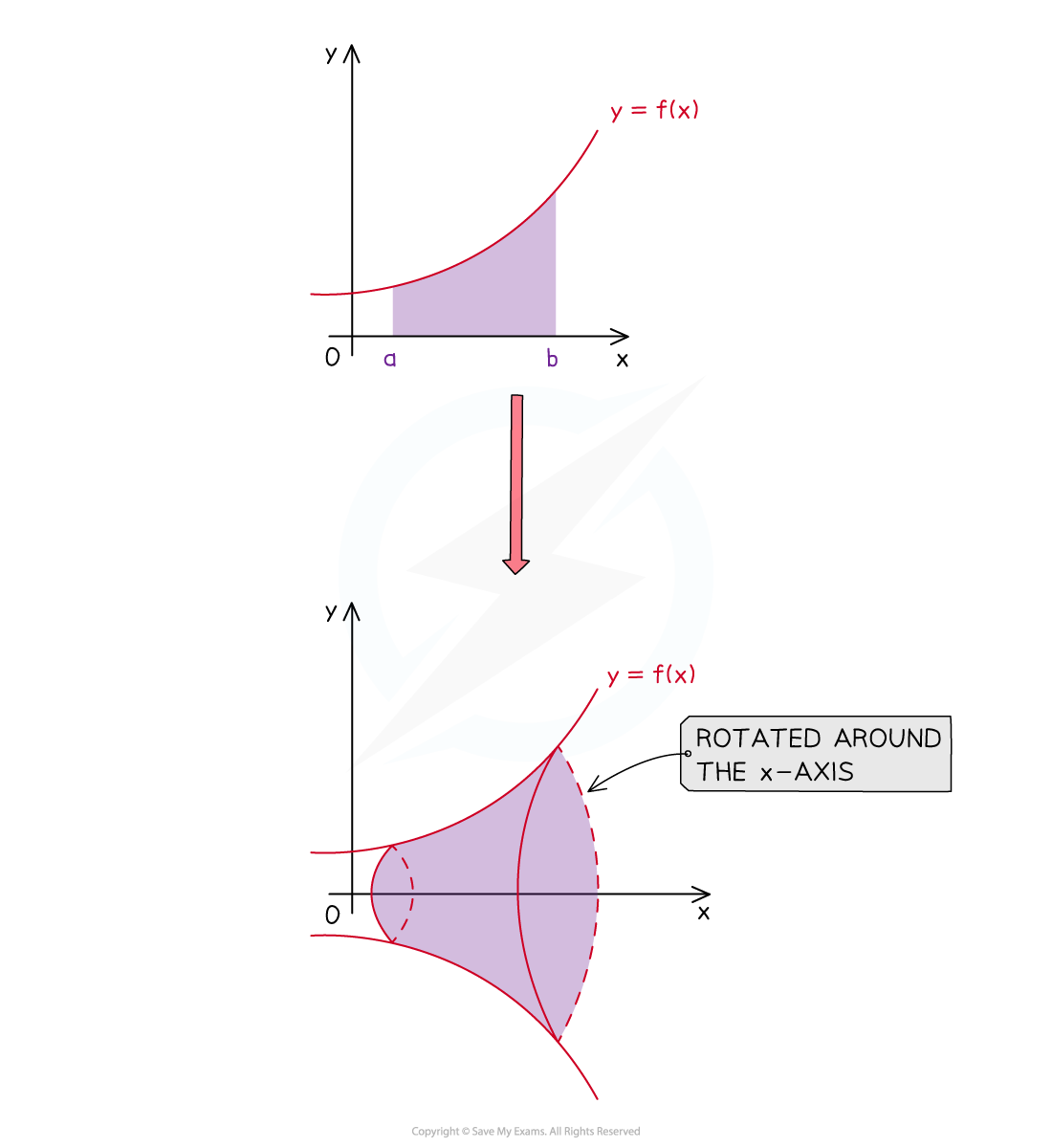
Graph rotating around x-axis to form a volume of revolution

Be careful – the ’front’ and ‘back’ of this solid are flat
- they were created from straight (vertical) lines
- 3D sketches can be misleading!

What is the formula for a volume of revolution about the x-axis?

The volume of revolution of a solid rotated $2 π$ radians ( $360 °$ ) about the $x$ -axis between $x = a$ and $x = b$ is given by:

$V = π \int_{a}^{b} y^{2} d x$

This is not given on the exam formula sheet, so you need to remember it
- Note that $π y^{2}$ is the area of the circular cross-section of the solid at any value of $x$
- That might help you remember the form of the volume integral
$y$ is a function of $x$
- i.e. $y = f (x)$
$x = a$ and $x = b$ are the equations of the (vertical) lines bounding the area
- $a < b$ ( $a$ is the 'left boundary' and $b$ is the 'right boundary')
- $x = a$ and $x = b$ may be given in the question
- one boundary may be the $y$ -axis ( $x = 0$ )
- the $x$ -axis intercepts of $y = f (x)$ may also be boundaries

How do I calculate the volume of revolution about the x-axis?

STEP 1
Identify the limits $a$ and $b$
- These may be given in the question
  - or be indicated on a graph in the question
- Sketching the graph of $y = f (x)$ can help if the graph is not provided
STEP 2
Square the function $y = f (x)$
- e.g. $y = x^{2} + 1 \Rightarrow y^{2} = {(x^{2} + 1)}^{2} = x^{4} + 2 x^{2} + 1$
- or $y = \sqrt{4 - x} \Rightarrow y^{2} = {(\sqrt{4 - x})}^{2} = 4 - x$
STEP 3
Evaluate the integral in the volume formula $V = π \int_{a}^{b} y^{2} d x$
- An answer may be required in exact form
  - i.e. as a multiple of $π$

Examiner Tips and Tricks

Don't panic if $y = f (x)$ involves a square root
- The square root will disappear when you find $y^{2}$
Don't forget to bring $π$ back in after working out the integral
- In my experience that is a very common student error

Worked Example

Find the volume of the solid of revolution formed by rotating the region bounded by the graph of $y = \sqrt{3 x^{2} + 2}$ , the coordinate axes and the line $x = 3$ by $2 π$ radians about the $x$ -axis. Give your answer as an exact value.

Start by finding the values of $a$ and $b$ for the formula

'Bounded by the coordinate axes' tells us that the $y$ -axis ( $x = 0$ ) is one boundary
The question tells us that $x = 3$ is the other one
So $a = 0$ and $b = 3$

If in doubt, drawing a sketch can help

Sketch of function for volume of revolution

Now square the function $y = f (x)$

$y^{2} = {(\sqrt{3 x^{2} + 2})}^{2} = 3 x^{2} + 2$

Substitute everything into $V = π \int_{a}^{b} y^{2} d x$

$V = π \int_{0}^{3} (3 x^{2} + 2) d x$

Work out the definite integral

$\begin{array}{rcl} \int_{0}^{3} (3 x^{2} + 2) d x & = & {[3 (\frac{x^{2 + 1}}{2 + 1}) + 2 x]}_{0}^{3} \\ = & {[x^{3} + 2 x]}_{0}^{3} \\ = & ({(3)}^{3} + 2 (3)) - ({(0)}^{3} + 2 (0)) \\ = & 33 - 0 \\ = & 33 \end{array}$

Put that value back into the volume formula

Don't forget to include the $π$ !

$V = 33 π$

The question asks for an exact value answer, so leave the answer in terms of $π$

Volume $= 33 π {units}^{3}$

Last updated: 20 October 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Areas Between CurvesNext:Kinematics Toolkit