Calculating Areas (Edexcel IGCSE Further Pure Maths)

Revision Note

Written by: Roger B

Reviewed by: Dan Finlay

Definite Integrals

What is a definite integral?

A definite integral is defined by the following formula
- $\int_{a}^{b} f^{'} (x) d x = {[f (x)]}_{a}^{b} = f (b) - f (a)$
  - i.e. integrate as usual to find $f (x)$
  - then substitute to find $f (b)$ and $f (a)$
  - and subtract $f (a)$ from $f (b)$ to find the value of the definite integral
- $a$ and $b$ are numbers and are called the integration limits
  - $a$ is the lower limit
  - $b$ is the upper limit
  - the integral is 'from $a$ to $b$ '
- A constant of integration (“ $+ c$ ”) is not needed with definite integrals
Note that the answer to a definite integral is a number
- The answer to an indefinite integral is another function

Examiner Tips and Tricks

Be careful when substituting in to find $f (b) - f (a)$
- It's quite easy to make mistakes here
- Especially when fractions and negative numbers are involved
Your calculator may be able to find the value of definite integrals
- You can use this to check your work
Look out for phrases in exam questions like "Use algebraic integration" or "Using calculus"
- These mean that full working out of the integral 'by hand' is required
- A calculator answer without working would not score marks

Worked Example

Show that

$\int_{2}^{4} 3 x (x^{2} - 2) d x = 144$

Start by expanding the brackets inside the integral

$\int_{2}^{4} (3 x^{3} - 6 x) d x$

Integrate as usual (here it's a 'powers of $x$ ' integration)

Write the answer in square brackets with the integration limits outside

$\begin{array}{rcl} \int_{2}^{4} (3 x^{3} - 6 x) d x & = & {[3 (\frac{x^{3 + 1}}{3 + 1}) - 6 (\frac{x^{1 + 1}}{1 + 1})]}_{2}^{4} \\ = & {[\frac{3}{4} x^{4} - 3 x^{2}]}_{2}^{4} \end{array}$

Now substitute 4 into that function
And subtract from it the function with 2 substituted in

$\begin{array}{rcl} {[\frac{3}{4} x^{4} - 3 x^{2}]}_{2}^{4} & = & (\frac{3}{4} {(4)}^{4} - 3 {(4)}^{2}) - (\frac{3}{4} {(2)}^{4} - 3 (2^{2})) \\ = & (192 - 48) - (12 - 12) \\ = & 144 - 0 \\ = & 144 \end{array}$

And that's the answer we were asked to show!

$\int_{2}^{4} 3 x (x^{2} - 2) d x = 144$

Calculating Areas with Definite Integrals

How can I calculate areas using definite integrals?

Region $R$ in the following diagram is the 'area under a curve' between $x = a$ and $x = b$
- It is the region bounded by
  - the curve $y = f (x)$
  - the $x$ -axis
  - and the lines $x = a$ and and $x = b$

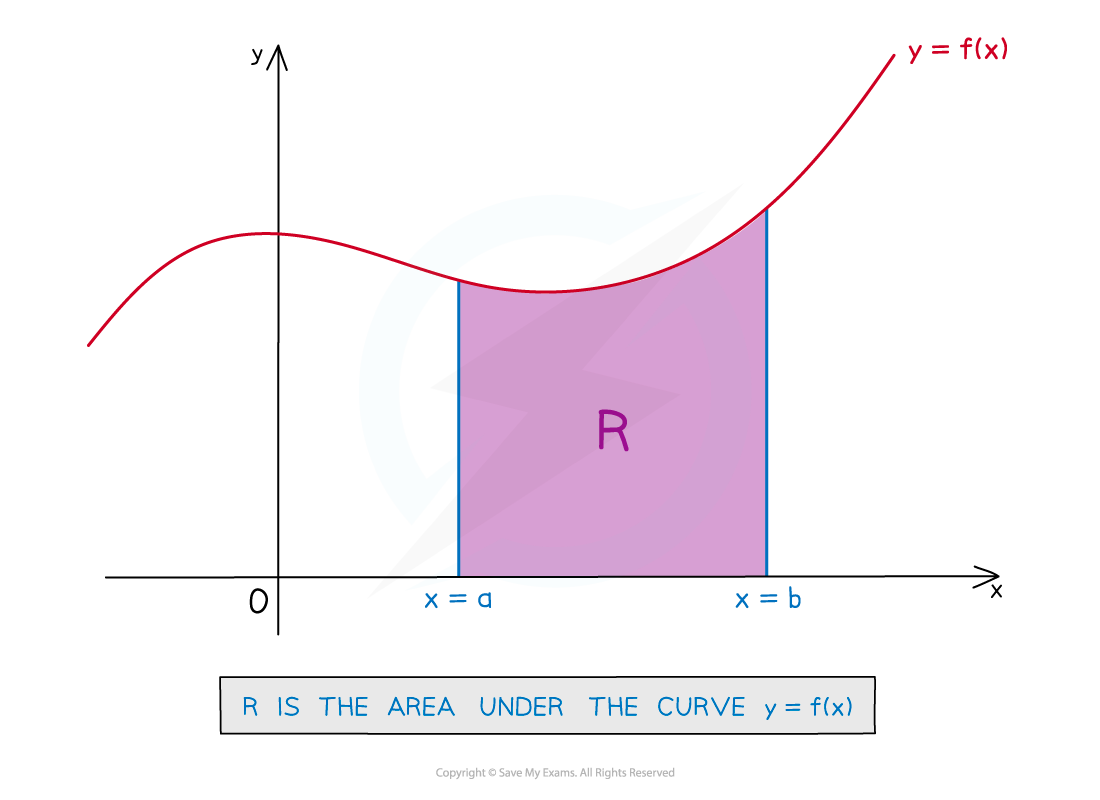
The exact area of a region like region $R$ in the diagram can be found by evaluating the definite integral
- $Area = \int_{a}^{b} f (x) d x$
  - i.e. definite integrals can be used as area calculators!
- Note that for this to work, $a$ must be 'on the left' and $b$ must be 'on the right'
  - i.e. $a \leq b$

How do I form a definite integral to find the area under a curve?

The curve $y = f (x)$ and the $x$ -axis should be obvious boundaries
- but the trick can be identifying $a$ and $b$
  - i.e. the lower and upper limits of the definite integral
If a diagram is given in the question, this can help locate the limits
- If a diagram is not given, then sketch one
The 'left' and 'right' boundaries may be vertical lines
- In that case their equations give the integral limits
  - $x = a$ and $x = b$
The $y$ -axis may be one of the (vertical) boundaries
- in that case one of the limits will be $x = 0$
The 'left' and 'right' boundaries don't have to be vertical lines
- One or both of them could be where $y = f (x)$ intercepts the $x$ -axis
  - i.e., one of the roots of the equation $f (x) = 0$
- In this case solve the equation $f (x) = 0$ to find the limit(s)

Examiner Tips and Tricks

Look out for questions that ask you to find an indefinite integral in one part
- where ' $+ c$ ' is needed in the answer
- then in a later part use the same integral as a definite integral
  - where ' $+ c$ ' is not needed
Add information to any diagram provided in the question
- axes intercepts
- values of limits
- mark and shade the area you’re trying to find
If no diagram is provided, sketch one!

Worked Example

The following diagram shows a part of the graph of the curve with equation $y = 3 + 2 x - x^{2}$ . The region labelled $R$ is bounded by the curve, the positive $y$ -axis, and the positive $x$ -axis.

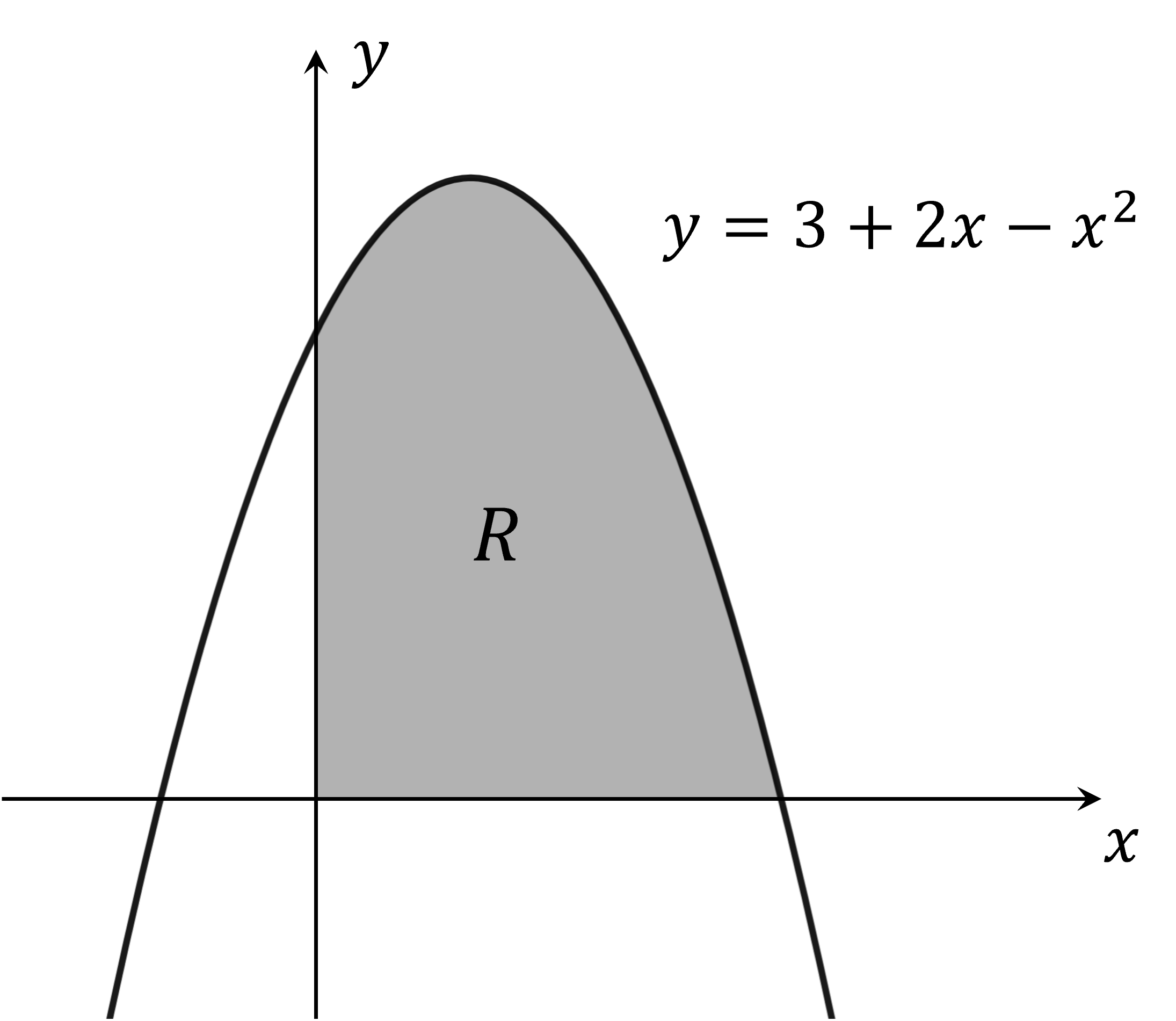
Find the exact area of region $R$ .

Start by finding the integration limits.

The $y$ -axis is the left boundary, so $x = 0$ will be the lower integration limit

The right boundary is where the curve intercepts the $x$ -axis
Solve the equation $y = 0$ to find its $x$ -coordinate

$\begin{array}{rcl} 3 + 2 x - x^{2} & = & 0 \\ x^{2} - 2 x - 3 & = & 0 \\ (x + 1) (x - 3) & = & 0 \end{array}$

$x = - 1 or x = 3$

We want the positive intercept, so the upper integral limit will be $x = 3$

Put all that info into the definite integral

$\begin{array}{rcl} Area & = & \int_{0}^{3} (3 + 2 x - x^{2}) d x \\ = & {[3 x + 2 (\frac{x^{1 + 1}}{1 + 1}) - (\frac{x^{2 + 1}}{2 + 1})]}_{0}^{3} \\ = & {[3 x + x^{2} - \frac{1}{3} x^{3}]}_{0}^{3} \\ = & (3 (3) + {(3)}^{2} - \frac{1}{3} {(3)}^{3}) - (3 (0) + {(0)}^{2} - \frac{1}{3} {(0)}^{3}) \\ = & (9 + 9 - 9) - (0 + 0 - 0) \\ = & 9 - 0 \\ = & 9 \end{array}$

$9 {units}^{2}$

Negative Integrals

What do we mean by a 'negative integral'

The answer to a definite integral is a number
- This number can be positive or negative (or zero!)
The area between a curve and the $x$ -axis may lie fully or partially below the $x$ -axis
- This occurs when the function $f (x)$ takes negative values within the boundaries of the area
A definite integral used to find such an area
- will be negative if the area is fully under the $x$ -axis
- possibly negative if the area is partially under the $x$ -axis
  - even if positive, the integral will not calculate the correct area in this case
  - the 'negative areas' will subtract from the 'positive areas'

How do I find the area under a curve when the curve is fully under the x-axis?

Area found with integration, entirely under the x-axis

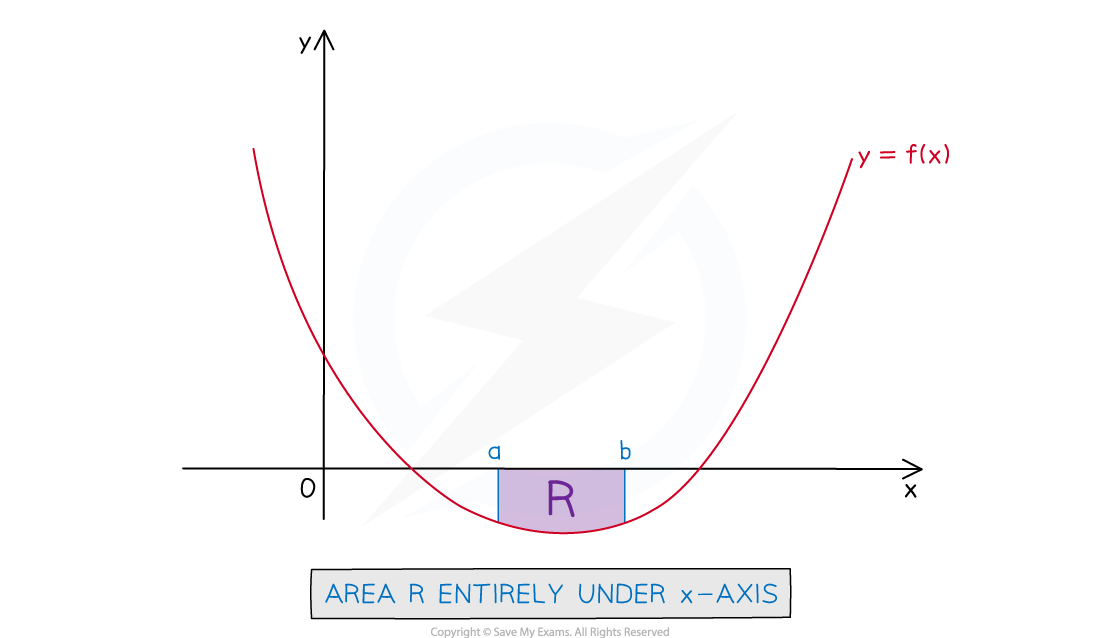
STEP 1
Write the definite integral to find the area as usual
- This may involve finding the lower and upper integration limits
STEP 2
The answer to the definite integral will be negative
- But the answer will have the same 'size' as the area
- So just remove the minus sign to get the area
  - e.g. if the value of the integral is $- 36$
  - then the area will be $36$ (square units)

How do I find the area under a curve when the curve is partially under the x-axis?

Area found with integration, partially under the x-axis

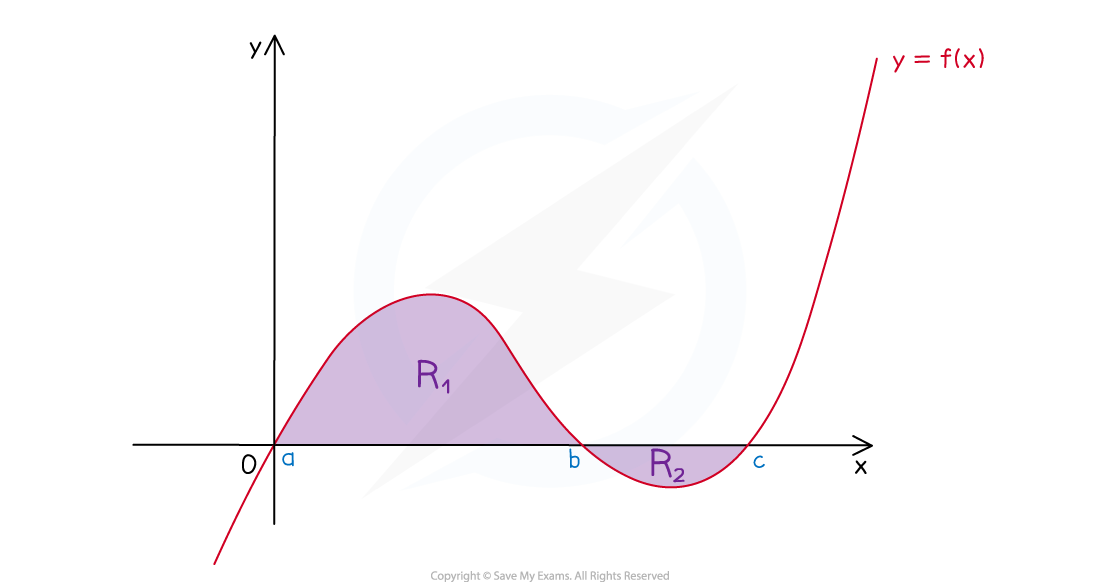
STEP 1
Split the area into parts
- the area(s) that are above the $x$ -axis
- and the area(s) that are below the $x$ -axis

STEP 2
Write the definite integral for each part
- This may involve finding the lower and upper integration limits for each part
  - e.g. solving $f (x) = 0$ to find where $y = f (x)$ crosses the $x$ -axis
STEP 3
Find the value of each definite integral separately
STEP 4
Change the negative values to positive
- Then find the total area by summing the 'positive versions' of each integral

Examiner Tips and Tricks

If no diagram is provided, sketch one
- This lets you see where the curve is above and below the $x$ -axis
- Then you can split up your integrals accordingly

Worked Example

The diagram below shows the graph of $y = f (x)$ , where $f (x) = (x + 4) (x - 1) (x - 5)$ .

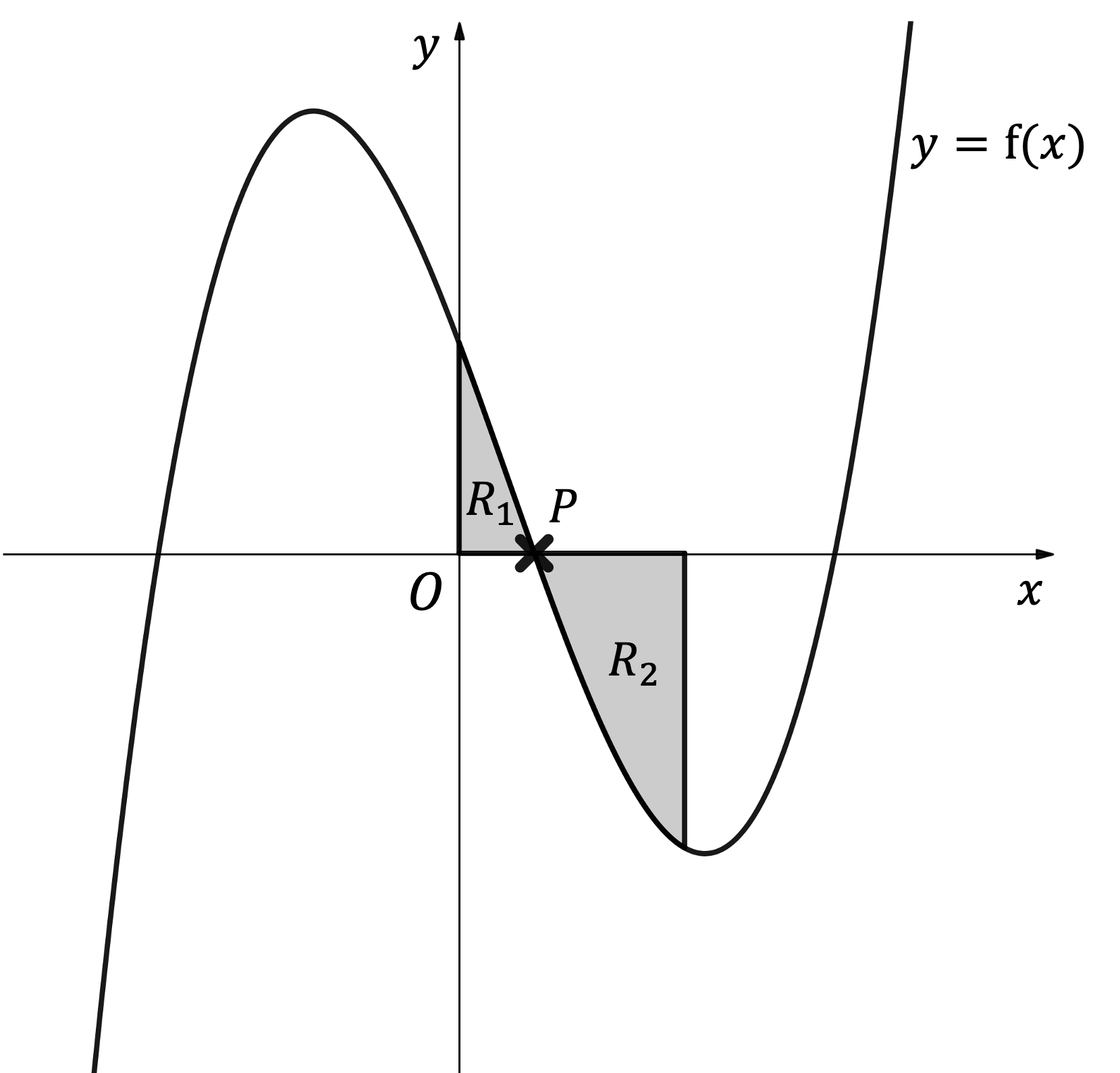
cubic graph for finding area using integration

The region $R_{1}$ is bounded by the curve $y = f (x)$ and the positive $x$ - and $y$ -axes.

The region $R_{2}$ is bounded by the curve $y = f (x)$ , the positive $x$ -axis, and the line $x = 3$ .

(a) Determine the coordinates of the point labelled $P$ .

That point is one of the $x$ -axis intercepts of the function

Solve $f (x) = 0$ to find what those area

$(x + 4) (x - 1) (x - 5) = 0$

$x = - 4, 1, 5$

It has to be positive, because the point is to the right of the origin
And it has to be less than 3, because it's to the left of the line $x = 3$
So it must be the intercept at $x = 1$

$(1, 0)$

(b) Find the exact total area of the shaded regions $R_{1}$ and $R_{2}$ .

$R_{1}$ is the region between $x = 0$ and $x = 1$

It lies totally above the $x$ -axis, so the definite integral will calculate the area directly

$\begin{array}{rcl} Area of R_{1} & = & \int_{0}^{1} (x + 4) (x - 1) (x - 5) d x \\ = & \int_{0}^{1} (x^{3} - 2 x^{2} - 19 x + 20) d x \\ = & {[\frac{1}{4} x^{4} - \frac{2}{3} x^{3} - \frac{19}{2} x^{2} + 20 x]}_{0}^{1} \\ = & (\frac{1}{4} {(1)}^{4} - \frac{2}{3} {(1)}^{3} - \frac{19}{2} {(1)}^{2} + 20 (1)) - (\frac{1}{4} {(0)}^{4} - \frac{2}{3} {(0)}^{3} - \frac{19}{2} {(0)}^{2} + 20 (0)) \\ = & (\frac{1}{4} - \frac{2}{3} - \frac{19}{2} + 20) - (0 - 0 - 0 + 0) \\ = & \frac{121}{12} - 0 \\ = & \frac{121}{12} \end{array}$

$R_{2}$ is the region between $x = 1$ and $x = 3$

It lies totally below the $x$ -axis, so the integral will give us the negative version of the area

$\begin{array}{rcl} - (Area of R_{2}) & = & \int_{1}^{3} (x^{3} - 2 x^{2} - 19 x + 20) d x \\ = & {[\frac{1}{4} x^{4} - \frac{2}{3} x^{3} - \frac{19}{2} x^{2} + 20 x]}_{1}^{3} \\ = & (\frac{1}{4} {(3)}^{4} - \frac{2}{3} {(3)}^{3} - \frac{19}{2} {(3)}^{2} + 20 (3)) - (\frac{1}{4} {(1)}^{4} - \frac{2}{3} {(1)}^{3} - \frac{19}{2} {(1)}^{2} + 20 (1)) - \\ = & (\frac{81}{4} - 18 - \frac{171}{2} + 60) - (\frac{1}{4} - \frac{2}{3} - \frac{19}{2} + 20) \\ = & - \frac{93}{4} - \frac{121}{12} \\ = & - \frac{400}{12} \end{array}$

So the area of $R_{2}$ is $\frac{400}{12}$ $(= \frac{100}{3})$

Add the two areas together to get the total area

$total area = \frac{121}{12} + \frac{400}{12} = \frac{521}{12}$

$\frac{521}{12} {units}^{2}$

Last updated: 20 October 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Constants of IntegrationNext:Areas Between Curves

Calculating Areas (Edexcel IGCSE Further Pure Maths)

Revision Note

Definite Integrals

What is a definite integral?

Examiner Tips and Tricks

Worked Example

Calculating Areas with Definite Integrals

How can I calculate areas using definite integrals?

How do I form a definite integral to find the area under a curve?

Examiner Tips and Tricks

Worked Example

Negative Integrals

What do we mean by a 'negative integral'

How do I find the area under a curve when the curve is fully under the x-axis?

How do I find the area under a curve when the curve is partially under the x-axis?

Examiner Tips and Tricks

Worked Example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Roger B

Author: Dan Finlay