Areas Between Curves (Edexcel IGCSE Further Pure Maths)

Revision Note

Written by: Roger B

Reviewed by: Dan Finlay

Area Between a Curve and a Line

What do we mean by 'area between a curve and a line'?

Areas whose boundaries include a curve and a (non-vertical) straight line can be found using integration
- For an area under a curve a definite integral will be needed
- For an area under a line the shape formed will be a trapezium or triangle
  - basic area formulae can be used rather than a definite integral
  - (although a definite integral would still work)
The area required could be the sum or difference of areas under the curve and line

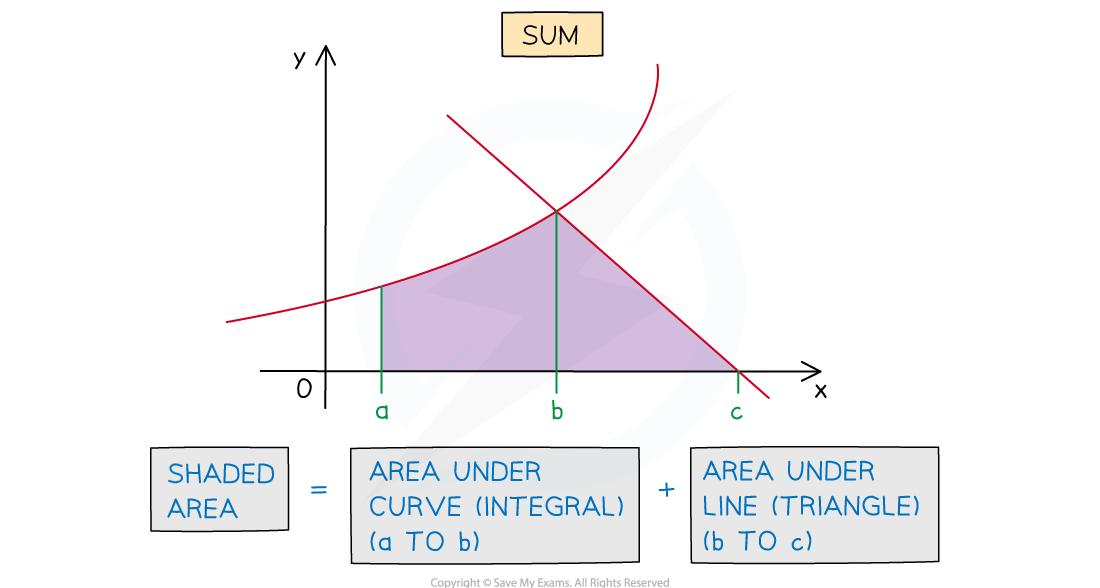
Sum of two areas under a curve and a line

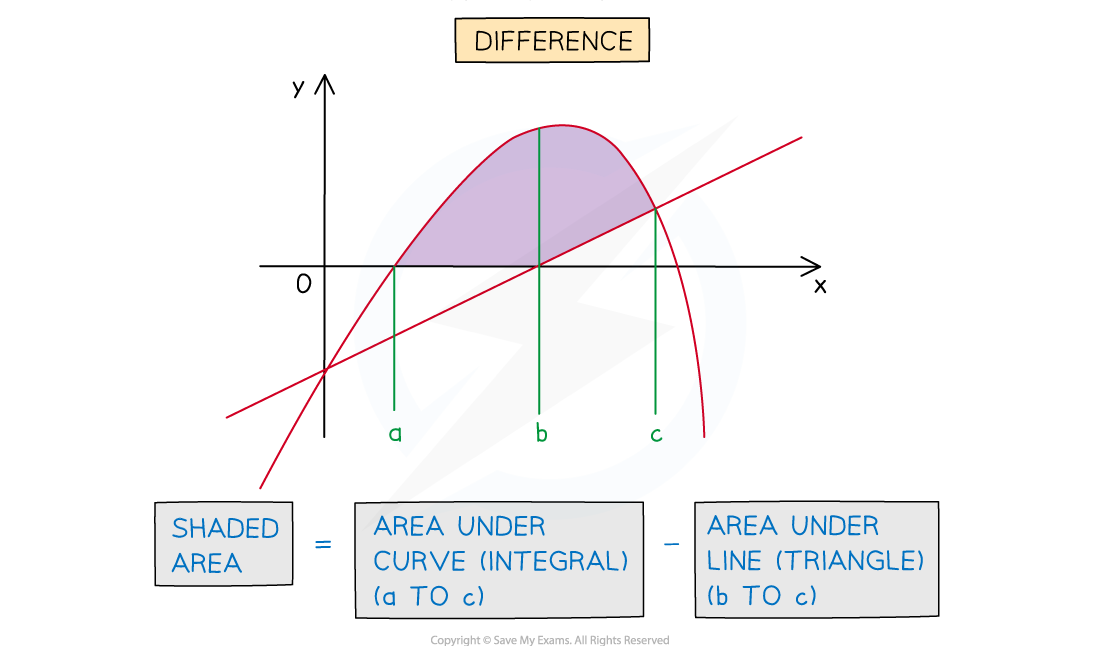
Difference between two areas below a curve and a line

How do I find the area between a curve and a line?

STEP 1
If not given, sketch the graphs of the curve and line on the same diagram
STEP 2
Find the intersections of the curve and the line
- If no diagram is given this will help identify the area(s) to be found
STEP 3
Determine whether the area required is a sum or difference
- Calculate the area under a curve using a integral of the form $\int_{a}^{b} y d x$
- Calculate the area under a line using
  - $A = \frac{1}{2} b h$ for a triangle
  - $A = \frac{1}{2} (a + b) h$ for a trapezium
    - For a trapezium, y-coordinates will be needed for a and b
    - and the height h will lie parallel to the x-axis
- Those areas will need to be added or subtracted, depending on the question
STEP 4
Evaluate the definite integral(s)
- Then find the sum or difference of areas as required

Examiner Tips and Tricks

Add information to any diagram provided
- intersections between lines and curves
- mark and shade the area you’re trying to find
If no diagram is provided, sketch one!

Worked Example

The region $R$ is bounded by the curve with equation $y = 10 x - x^{2} - 16$ and the line with equation $y = 8 - x$ .

(a) Sketch the graphs of the curve and the line on the same set of axes.

Be sure to Identify and label the region $R$ on your sketch, and indicate the points of intersection between the curve and the line. You may assume without proof that the curve's $x$ -axis intercepts all lie on the positive $x$ -axis.

Because of the minus sign in front of $x^{2}$ , the curve will be an 'upside down u-shaped' parabola

We need to find the points of intersection of the curve and line
Set their equations equal and solve to find the $x$ -coordinates

$\begin{array}{rcl} 8 - x & = & 10 x - x^{2} - 16 \\ x^{2} - 11 x + 24 & = & 0 \\ (x - 3) (x - 8) & = & 0 \end{array}$

$x = 3 or x = 8$

So the curve and line intersect when $x = 3$ and when $x = 8$

Substitute into the equation of the line to find the corresponding $y$ -coordinates

$x = 3 : y = 8 - 3 = 5 x = 8 : y = 8 - 8 = 0$

So the points of intersection are $(3, 5)$ and $(8, 0)$

That gives us enough information to sketch the graphs

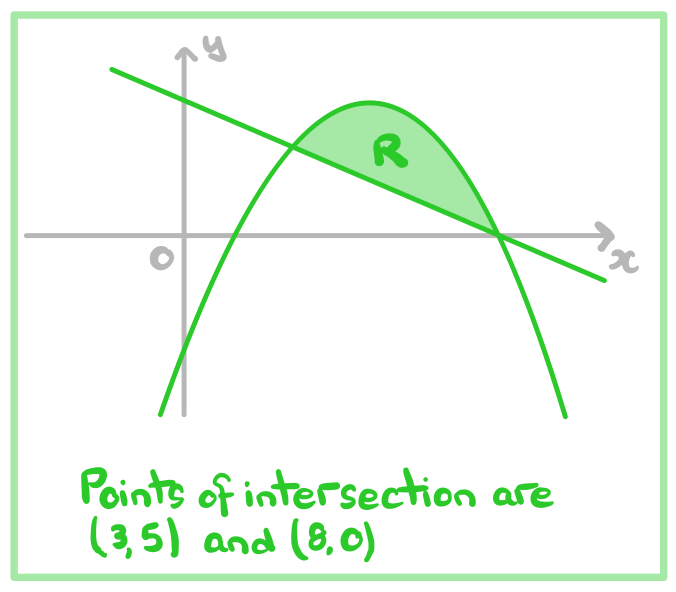
(b) Find the area of region $R$

Here we're going to need a difference of areas: (area under curve) $-$ (area under line)

The area under the line is a right-angled triangle with vertices at $(3, 0)$ , $(3, 5)$ and $(8, 0)$

So the height is $5 - 0 = 5$ and the base is $8 - 3 = 5$

$Area of triangle = \frac{1}{2} \times 5 \times 5 = \frac{25}{2}$

For the area under a curve we need to use a definite integral between $x = 3$ and $x = 8$

$\begin{array}{rcl} Area under the curve & = & \int_{3}^{8} (10 x - x^{2} - 16) d x \\ = & {[5 x^{2} - \frac{1}{3} x^{3} - 16 x]}_{3}^{8} \\ = & (5 {(8)}^{2} - \frac{1}{3} {(8)}^{3} - 16 (8)) - (5 {(3)}^{2} - \frac{1}{3} {(3)}^{3} - 16 (3)) \\ = & (320 - \frac{512}{3} - 128) - (45 - 9 - 48) \\ = & \frac{64}{3} - (- 12) \\ = & \frac{100}{3} \end{array}$

For the area of $R$ , subtract the area of the triangle from the area under the curve

$Area of region R = \frac{100}{3} - \frac{25}{2} = \frac{125}{6}$

$\frac{125}{6} {units}^{2}$

Area Between 2 Curves

What do we mean by 'area between two curves'?

Areas whose boundaries include two curves can be found by integration
- The area between two curves will be the difference of the areas under the two curves
  - both areas will require a definite integral
- Finding points of intersection may involve a more awkward equation than solving for a curve and a line

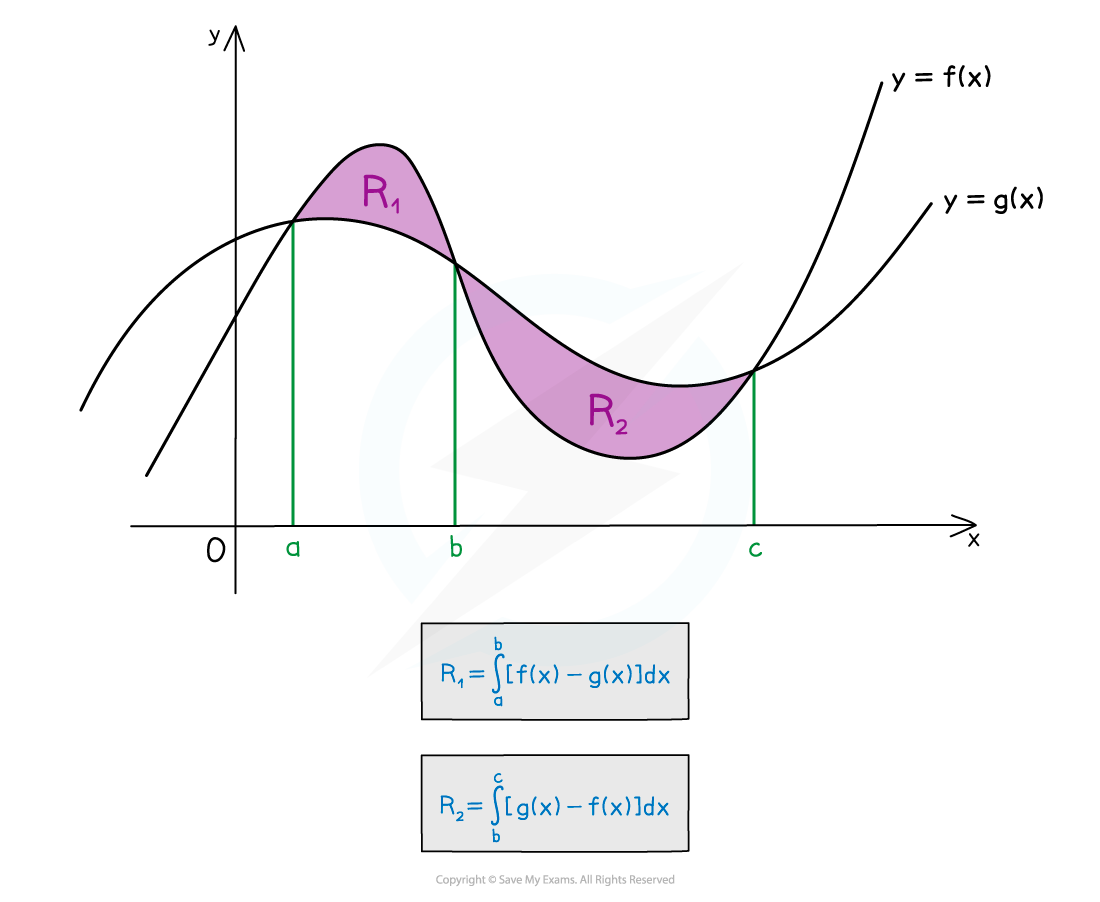
How do I find the area between two curves?

STEP 1
If not given, sketch the graphs of both curves on the same diagram
STEP 2
If not given, find the intersections of the two curves
- These are needed to identify the area(s) to be calculated
- and also to set up the correct integrals
STEP 3
Determine which curve is the ‘upper’ boundary for each region
- For each region, the area is given by definite integral of the form $\int_{a}^{b} (y_{1} - y_{2}) d x$
  - $y_{1}$ is the function forming the ‘upper’ boundary
  - $y_{2}$ is the function forming the ‘lower’ boundary
- Be careful when there is more than one region
  - Which functions form the ‘upper’ and ‘lower’ boundaries can change

STEP 4
Evaluate the definite integral(s)
- If there is more than one region, add their areas together to find the total area
- As long as ' $y_{1}$ ' in the integrals is always the upper function
  - then $y_{1} - y_{2} \geq 0$
  - This means you don't have to worry about negative integrals
  - even if part or all of the area between the curves is below the x-axis

Examiner Tips and Tricks

Add information to any given diagram as you work through a question
- intersections between curves
- mark and shade the area you're trying to find
If no diagram is provided sketch one

Worked Example

The diagram below shows the curves with equations $y = f (x)$ and $y = g (x)$ , where $f (x) = (x - 2) {(x - 3)}^{2}$ and $g (x) = x^{2} - 5 x + 6$ .

Find the area of the shaded region.

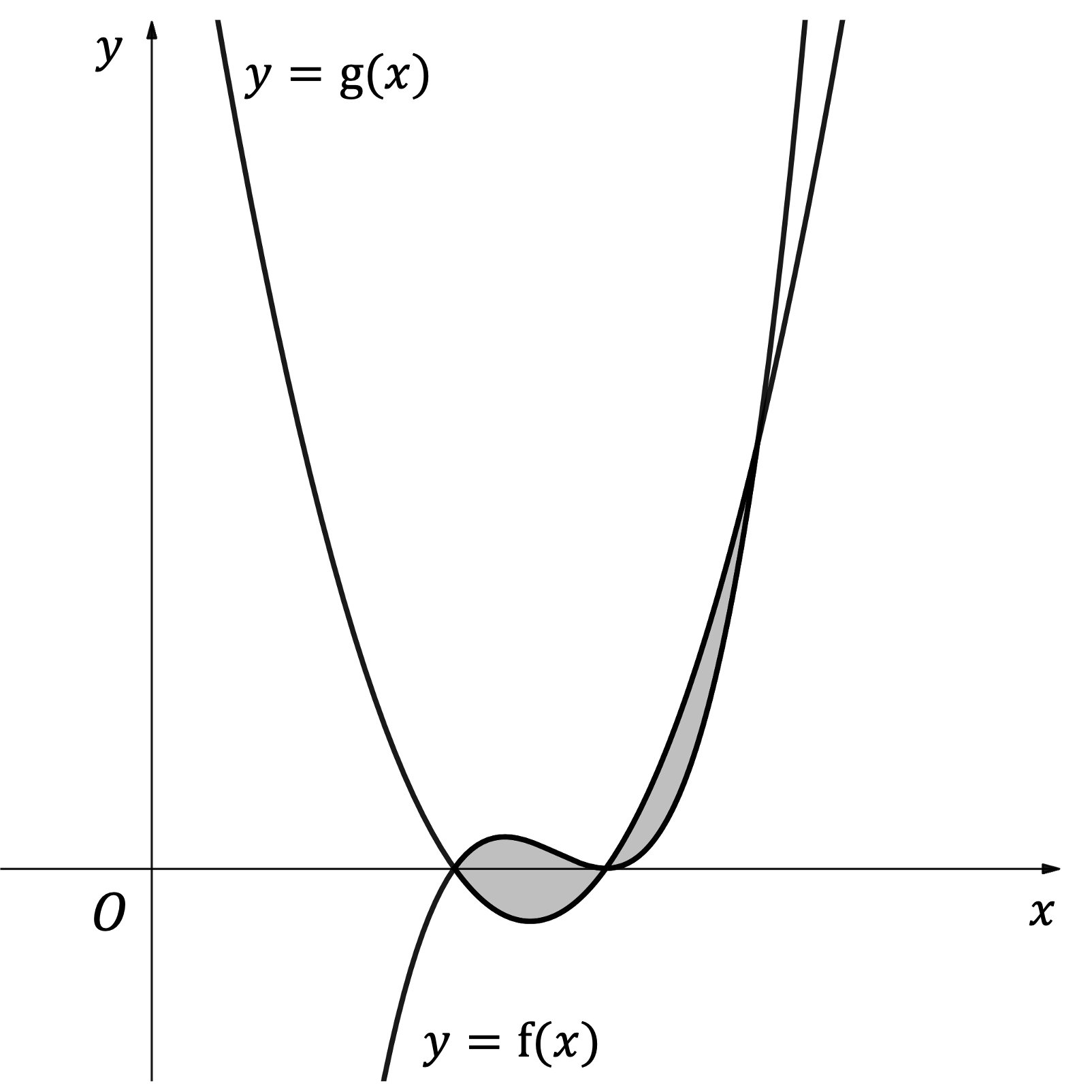
Areas formed between a cubic and a quadratic

Start by finding the points of intersection

Set the equations of the curves equal to each other, and solve to find the $x$ -coordinates

$(x - 2) {(x - 3)}^{2} = x^{2} - 5 x + 6$

It's tempting to expand the brackets on the left-hand side of the equation
Actually. here it will be more useful to factorise the right-hand side

$\begin{array}{rcl} (x - 2) {(x - 3)}^{2} & = & (x - 2) (x - 3) \\ (x - 2) {(x - 3)}^{2} - (x - 2) (x - 3) & = & 0 \\ (x - 2) (x - 3) ((x - 3) - 1) & = & 0 \\ (x - 2) (x - 3) (x - 4) & = & 0 \end{array}$

$x = 2, 3 or 4$

Note that we don't need to know the corresponding $y$ -coordinates here!

We have two regions here

The first region is from $x = 2$ to $x = 3$ , and $f (x)$ is the 'upper curve'

$\begin{array}{rcl} Region 1 & = & \int_{2}^{3} ((x - 2) {(x - 3)}^{2} - (x^{2} - 5 x + 6)) d x \\ = & \int_{2}^{3} (x^{3} - 9 x^{2} + 26 x - 24) d x \\ = & {[\frac{1}{4} x^{4} - 3 x^{3} + 13 x^{2} - 24 x]}_{2}^{3} \\ = & (\frac{1}{4} {(3)}^{4} - 3 {(3)}^{3} + 13 {(3)}^{2} - 24 (3)) - (\frac{1}{4} {(2)}^{4} - 3 {(2)}^{3} + 13 {(2)}^{2} - 24 (2)) \\ = & (\frac{81}{4} - 81 + 117 - 72) - (4 - 24 + 52 - 48) \\ = & - \frac{63}{4} - (- 16) \\ = & \frac{1}{4} \end{array}$

The second region is from $x = 3$ to $x = 4$ and $g (x)$ is the 'upper curve'

$\begin{array}{rcl} Region 2 & = & \int_{3}^{4} ((x^{2} - 5 x + 6) - (x - 2) {(x - 3)}^{2}) d x \\ = & \int_{3}^{4} (- x^{3} + 9 x^{2} - 26 x + 24) d x \\ = & {[- \frac{1}{4} x^{4} + 3 x^{3} - 13 x^{2} + 24 x]}_{3}^{4} \\ = & (- \frac{1}{4} {(4)}^{4} + 3 {(4)}^{3} - 13 {(4)}^{2} + 24 (4)) - (- \frac{1}{4} {(3)}^{4} + 3 {(3)}^{3} - 13 {(3)}^{2} + 24 (3)) \\ = & (- 64 + 192 - 208 + 96) - (- \frac{81}{4} + 81 - 117 + 72) \\ = & 16 - \frac{63}{4} \\ = & \frac{1}{4} \end{array}$

Now just add the two areas together to get the total area

$Total area = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}$

Area of the shaded region $= \frac{1}{2} {units}^{2}$

Last updated: 20 October 2024

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Previous:Calculating AreasNext:Volumes of Revolution

Areas Between Curves (Edexcel IGCSE Further Pure Maths)

Revision Note

Area Between a Curve and a Line

What do we mean by 'area between a curve and a line'?

How do I find the area between a curve and a line?

Examiner Tips and Tricks

Worked Example

Area Between 2 Curves

What do we mean by 'area between two curves'?

How do I find the area between two curves?

Examiner Tips and Tricks

Worked Example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Roger B

Author: Dan Finlay