IGCSEFurther MathsCambridge (CIE)Additional MathsRevision NotesTrigonometryTrigonometryTrigonometric Functions

Trigonometric Functions (Cambridge (CIE) IGCSE Additional Maths): Revision Note

Exam code: 0606

Written by: Amber

Reviewed by: Dan Finlay

Updated on 2 July 2026

Trigonometric functions

What are the trigonometric functions?

The three standard trigonometric functions are: sine, cosine and tangent
The functions are many-to-one mappings
- They do not have inverses unless their domain is restricted

Function	Notation	Domain	Range
Sine	$\sin (x)$	$x \in ℝ$	$- 1 \leq \sin (x) \leq 1$
Cosine	$\cos (x)$	$x \in ℝ$	$- 1 \leq \cos (x) \leq 1$
Tangent	$\tan (x)$	$\begin{array}{l} x \in ℝ \\ x \neq \pm 90 °, \pm 270 °, \pm 450 °, . . . (in degrees) \\ x \neq \pm \frac{π}{2}, \pm \frac{3 π}{2}, \pm \frac{5 π}{2}, . . . (in radians) \end{array}$	$\tan (x) \in ℝ$

How can I use the trigonometric functions with right-angled triangles?

The three trigonometric functions sine, cosine and tangent give the ratios of side lengths in right-angled triangles
For an acute angle in a right-angled triangle:
- Sine of the angle is the length of the side opposite the angle divided by the hypotenuse
- Cosine of the angle is the length of the side adjacent to the angle divided by the hypotenuse
- Tangent of the angle is the length of the opposite side divided by the length of the adjacent side
You can use the acronym SOHCAHTOA to help you remember these

The trig functions in relation to the sides of a right-angled triangle

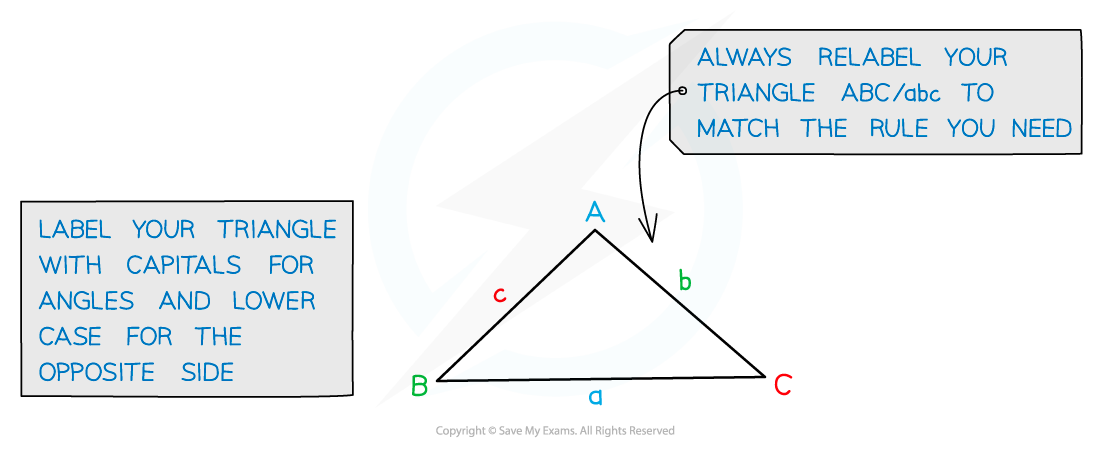
How can I use the trigonometric functions with non-right-angled triangles?

You can find missing angles and the lengths of missing sides using the sine rule and the cosine rule
You can also use the area formula

The formula for the sine rule, cosine rule and area of a triangle

Non-Right-Angled Triangles Diagram 1b, A Level & AS Level Pure Maths Revision Notes

Non-Right-Angled Triangles Diagram 1c, A Level & AS Level Pure Maths Revision Notes

Non-Right-Angled Triangles Diagram 1d, A Level & AS Level Pure Maths Revision Notes

Reciprocal trig functions

What are the reciprocal trig functions?

There are three reciprocal trig functions that each correspond to either sin, cos or tan
- Secant (sec x)
  - $\sec x = \frac{1}{\cos x}$
- Cosecant (cosec x)
  - $cosec x = \frac{1}{\sin x}$
- Cotangent (cot x)
  - $\cot x = \frac{1}{\tan x}$
A good way to remember which function is which is to look at the third letter in each of the reciprocal trig functions
- cot x is 1 over tan x etc
Each of the reciprocal trig functions are undefined for certain values of x
- sec x is undefined for values of x for which cos x = 0
- cosec x is undefined for values of x for which sin x = 0
- cot x is undefined for values of x for which tan x = 0
  - When tan x is undefined, cot x = 0
Be careful not to confuse the reciprocal trig functions with the inverse trig functions
- $\sin^{- 1} x \neq \frac{1}{\sin x}$

Worked Example

Without the use of a calculator, find the values of

a) $\sec \frac{π}{6}$

The third letter of sec is c so it is the reciprocal of cos.

$\sec (\frac{π}{6}) = \frac{1}{\cos (\frac{π}{6})}$

Write down the value of $\cos (\frac{π}{6})$ .

$\sec (\frac{π}{6}) = \frac{1}{(\frac{\sqrt{3}}{2})}$

Simplify.

$\sec (\frac{π}{6}) = \frac{2}{\sqrt{3}} or \frac{2 \sqrt{3}}{3}$

b) $\cot 45 °$

The third letter of cot is t so it is the reciprocal of tan.

$\cot (45 °) = \frac{1}{\tan (45 °)}$

Write down the value of tan(45°).

$\cot (45 °) = \frac{1}{1}$

$\cot (45 °) = 1$

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

Beth
IGCSE Student

This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

Fathima
A Level Student

Incredible! SO worth my money, the revision notes have everything I need to know and are so easy to understand. I actually enjoy revising! It makes me feel a lot more confident for my GCSEs in a few months.

Kate
GCSE Student

Absolutely brilliant, both my girls used it for A levels and GCSE. It's saves on paper copies, also beneficial exam questions ranked from easy to hard. It's removed a lot of stress from the exams.

Sameera
Parent

Just to say that your resources are the best I have seen and I have been teaching chemistry at different levels for about 40 years

Mark
Chemistry Teacher

Excellent