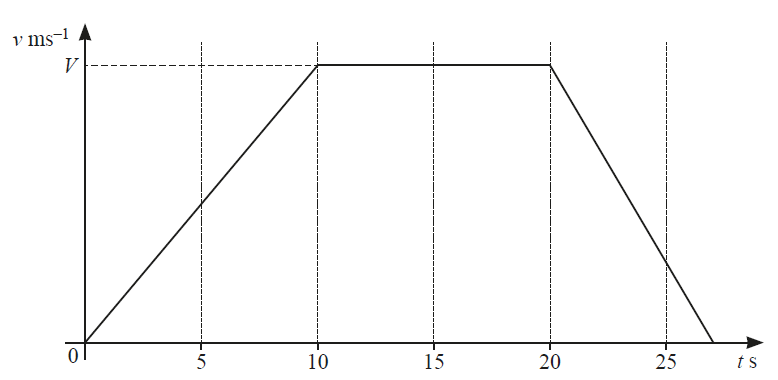
The diagram shows the velocity–time graph for a particle travelling in a straight line with velocity
at time
. The particle accelerates at
for the first 10 s of its motion and then travels at constant velocity,
, for
. The particle then decelerates at a constant rate and comes to rest. The distance travelled during the interval
.
(i) Find the value of .
[1]
(ii) Find the velocity of when
.
[3]
(iii) Find the value of when
comes to rest.
[3]
Did this page help you?




