Introduction to Vectors (Cambridge (CIE) IGCSE Additional Maths) : Revision Note
Did this video help you?
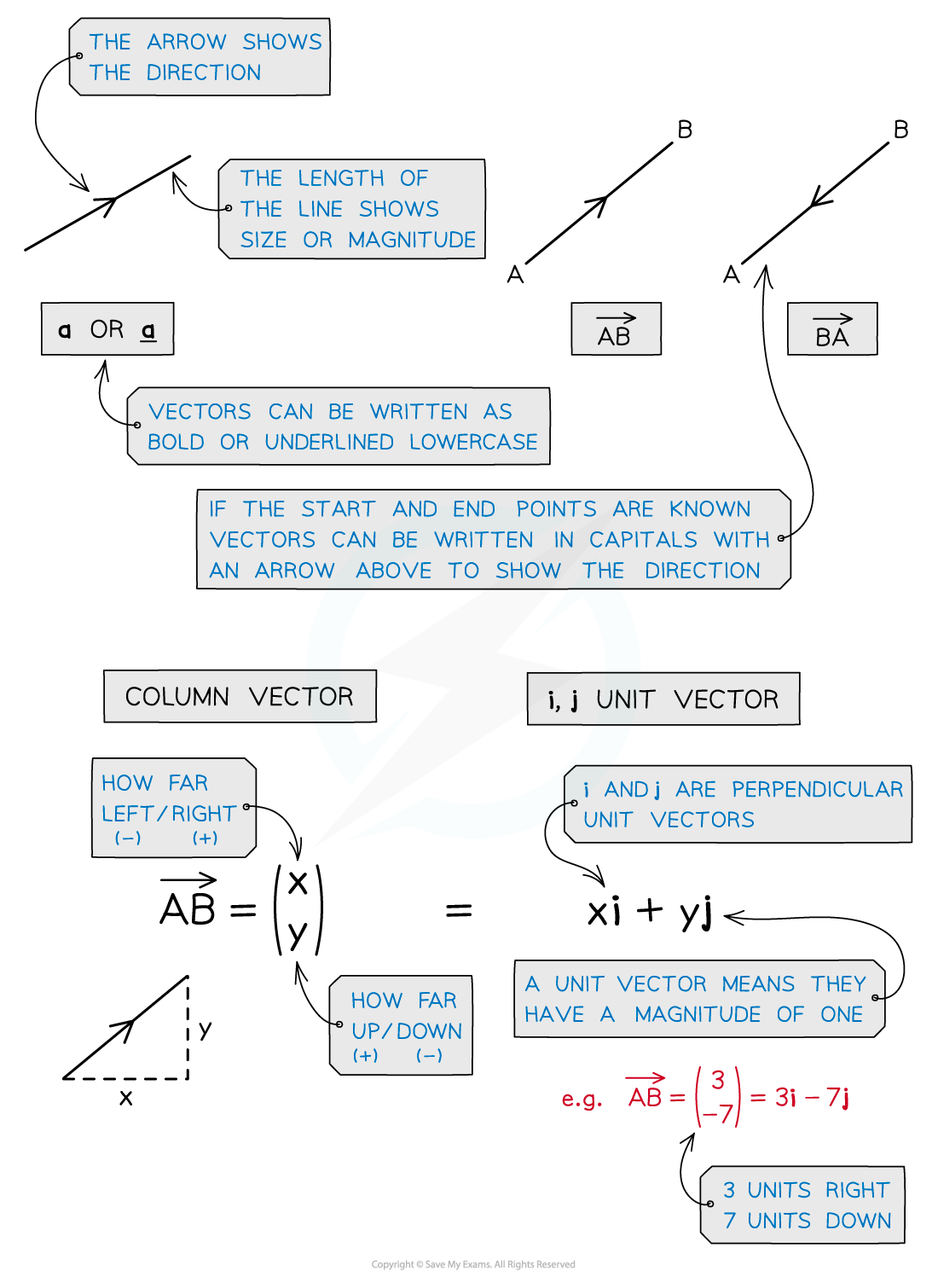
Basic Vectors
What is a vector?
Vectors represent a movement of a certain magnitude (size) in a given direction
For example: two objects with velocities of 7 m/s and ‑7 m/s are travelling at the same speed but in opposite directions
You should have already come across vectors when translating functions of graphs
They appear in many contexts of maths including mechanics for modelling forces
A vector in two directions has components in the direction of the x- and y- axes
Vector quantities can have positive or negative components
Vectors can be represented in different ways such as a column vector or as an i and j unit vector
Some examples of vector quantities you may come across are displacement, velocity or acceleration
Examiner Tips and Tricks
Think of vectors like a journey from one place to another
Diagrams can help, if there isn’t one, draw one
In your exam you can’t write in bold so should underline your vector notation
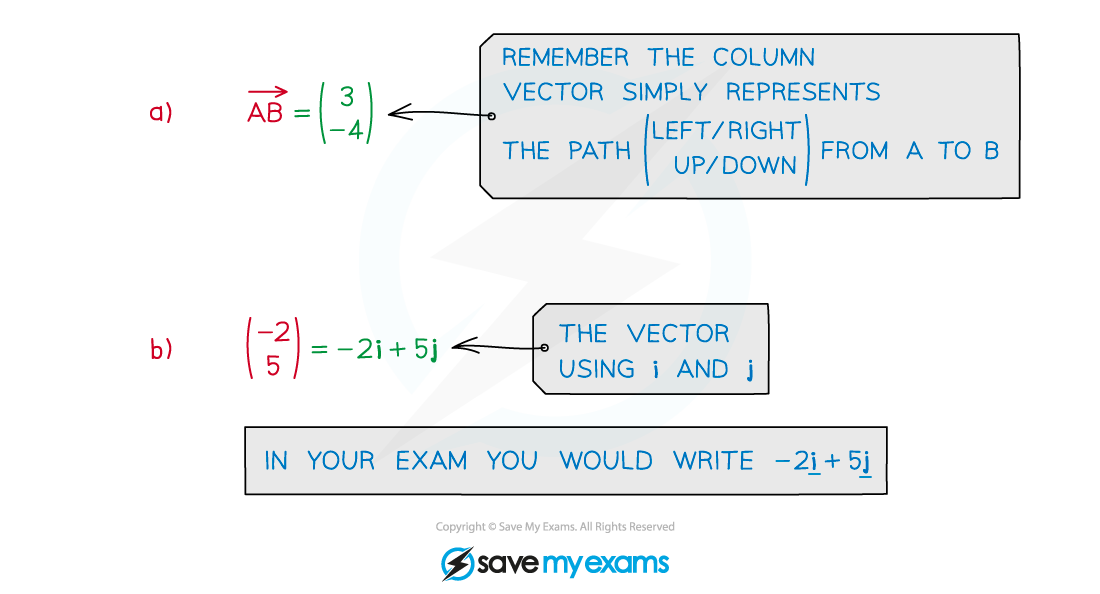
Worked Example

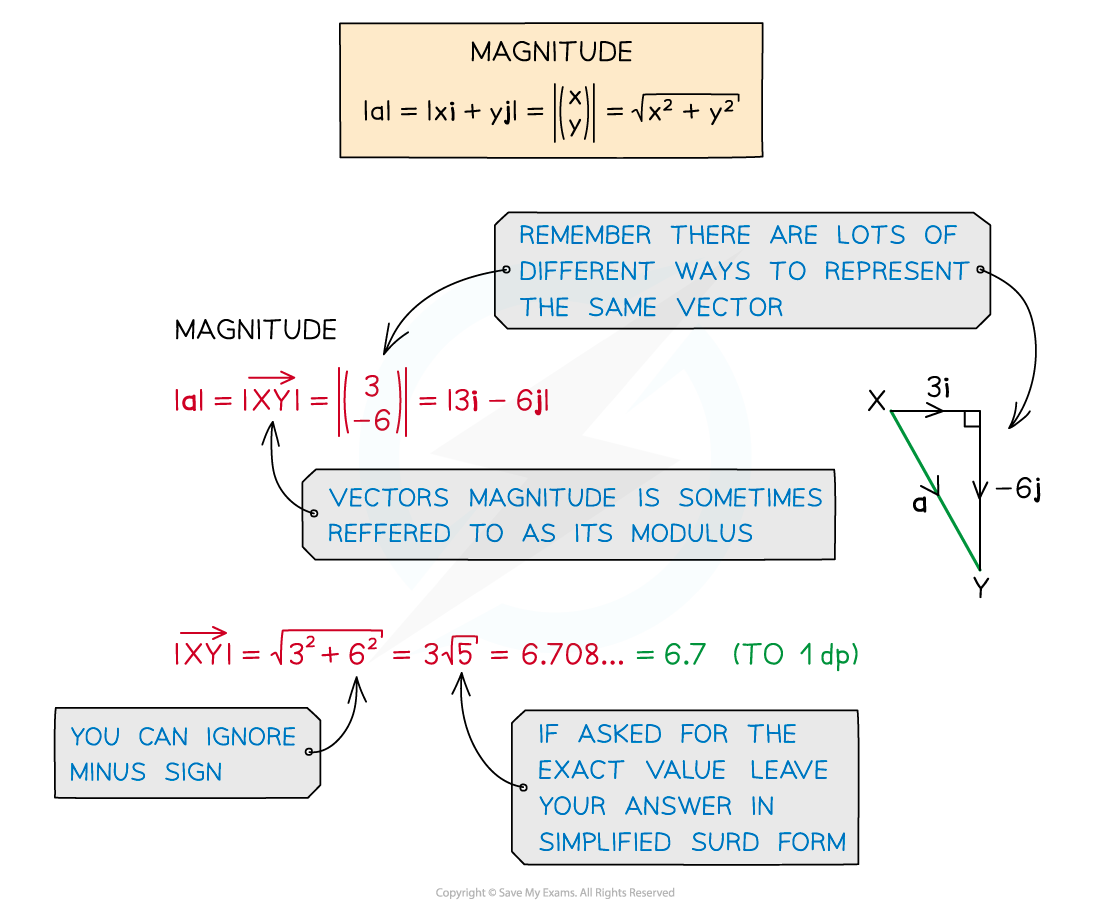
Magnitude of a Vector
How do you find the magnitude of a vector?
The magnitude of a vector tells us its size or length
The magnitude of the vector
is denoted
The magnitude of the vector a is denoted |a|
The magnitude of a vector can be found using Pythagoras’ theorem
The magnitude of a vector
is found using
where
What is a unit vector?
A unit vector has a magnitude of 1
The vectors
and
are unit vectors
the direction of
is in the positive
-direction
the direction of
is in the positive
-direction
To find a unit vector in the direction of a given vector divide the vector by its magnitude
Examiner Tips and Tricks
Finding the magnitude of a vector is the same as finding the distance between two coordinates
Commit the formula to memory and be prepared to use it in the exam
Worked Example
A vector .
a) Find .
is the magnitude of the vector, so use Pythagoras' theorem.
b) Find the unit vector in the direction of .
For a unit vector, divide the vector by its magnitude, which was found in part (a).
The unit vector in the direction of is
.
Did this video help you?
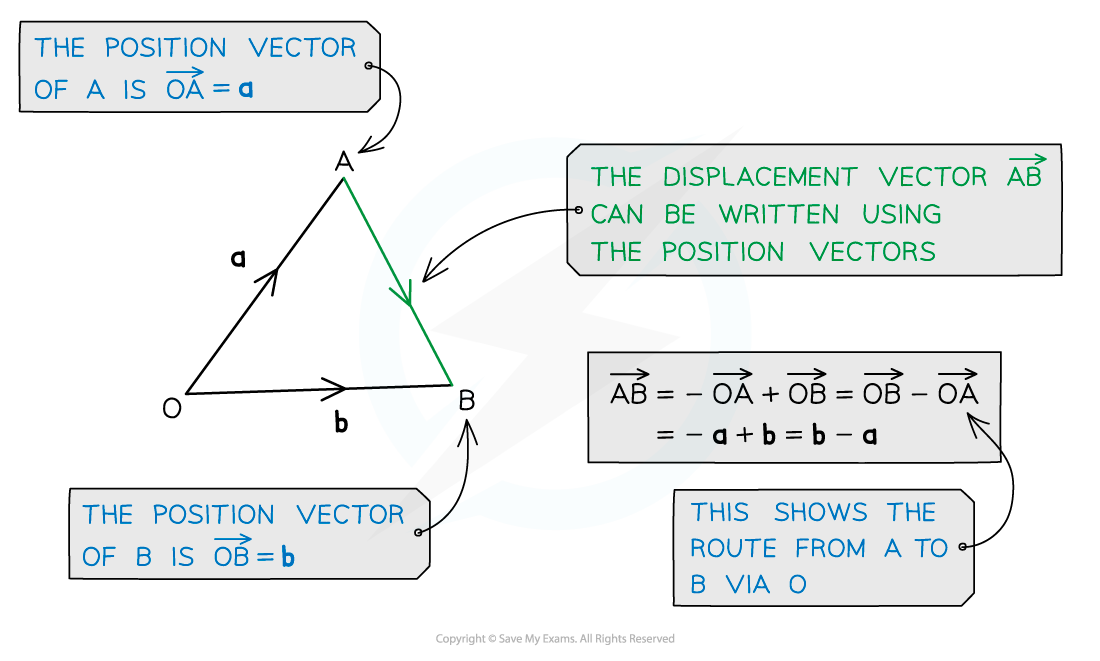
Position Vectors
What is a position vector?
Position vectors describe the position of a point in relation to the origin
They are different to displacement vectors which describe the direction and distance between any two points
The position vector of point A is written with the notation a =
The origin is always denoted O
The individual components of a position vector are the coordinates of its end point
For example the point with coordinates (3, -2) has position vector 3i – 2j
How do I find the distance between two points using vectors?
The distance between two points is the magnitude of the vector between them

How do I find the magnitude of a displacement vector?
You can use coordinate geometry to find magnitudes of displacement vectors from A to B
From the position vectors of A and B you know their coordinates
If
, then point A has coordinates
If
, then point B has coordinates
The distance between two points is given by
So
For example, if points A and B have position vectors
and
respectively
then
Alternatively, you could find
by
first using
to find
in vector form
and then calculating its magnitude directly
See the Worked Example below
Examiner Tips and Tricks
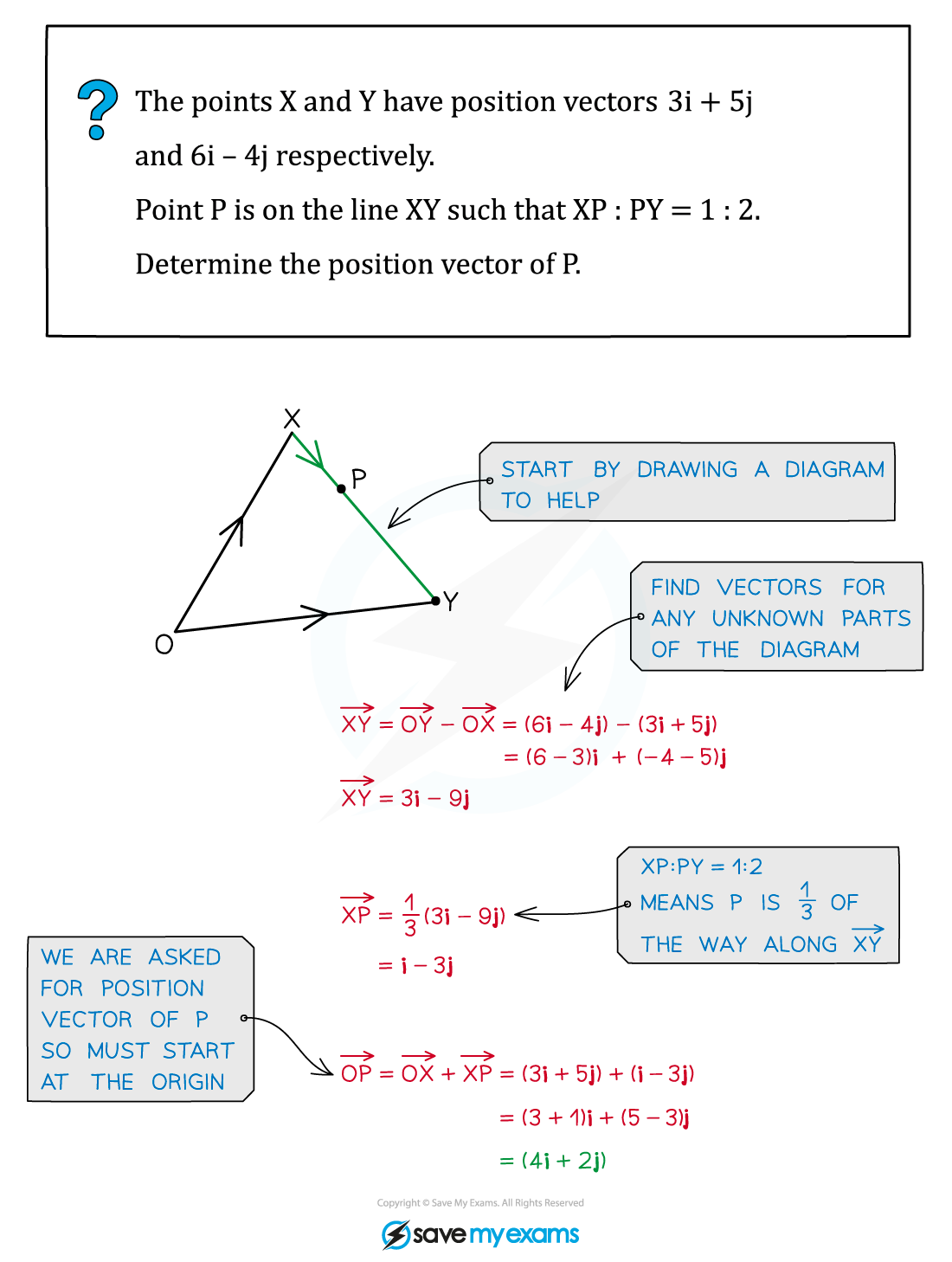
Remember if asked for a position vector, you must find the vector all the way from the origin
Diagrams can help, if there isn’t one, draw one
Worked Example

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
