Revision NotesExam QuestionsPast Papers
IGCSEFurther MathsCambridge (CIE)Additional MathsRevision NotesTrigonometryTrigonometryTrigonometric Proof

Trigonometric Proof (Cambridge (CIE) IGCSE Additional Maths) : Revision Note

Last updated

Trigonometric Proof

Proving trigonometric identities

  • You can use trigonometric identities you already know to prove new identities

  • Make sure you know the simple trigonometric identities and further trigonometric identities

    • sin squared theta plus cos squared theta equals 1

    • fraction numerator sin theta over denominator cos theta end fraction equals tan theta

    • 1 plus tan squared theta equals sec squared theta

    • 1 plus cot squared theta equals cosec squared theta

  • To prove an identity start on one side and proceed step by step until you get to the other side

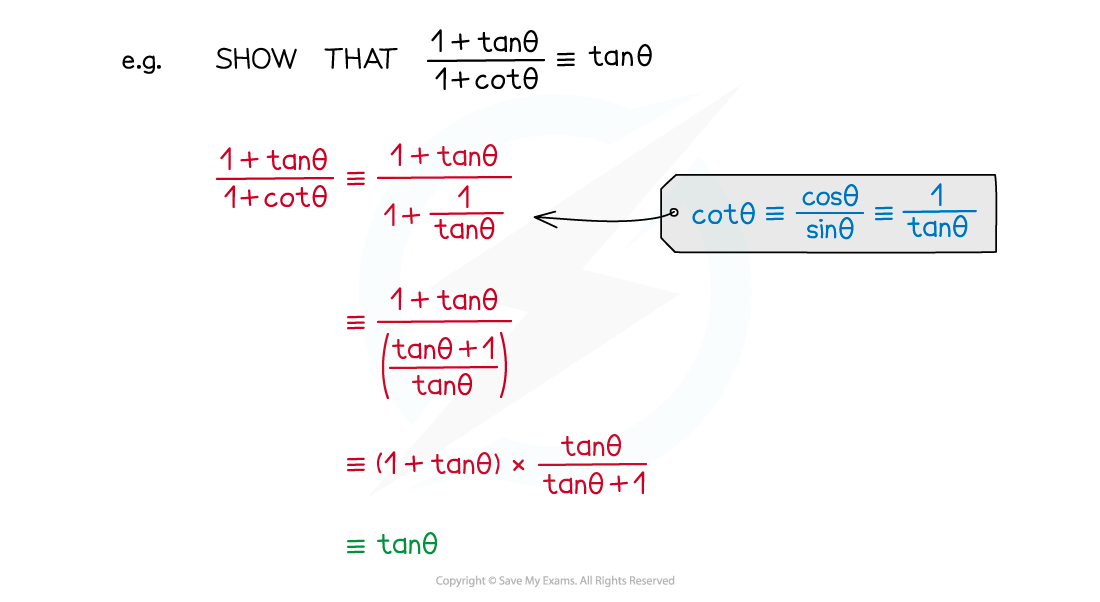
    • e.g. to prove that open parentheses sin theta plus cos theta close parentheses squared equals 1 plus 2 sin theta cos theta

    • Start with the left hand side, and expand

      • sin squared theta space plus space cos squared theta space plus space 2 sin theta cos theta

    • Simplify using the identity sin squared theta plus cos squared theta equals 1

      • 1 space plus space 2 sin theta cos theta

    • This is now equal to the expression on the right, so the statement has been proven

  • Make sure you are confident handling fractions and fractions-within-fractions

Example including a fraction within a fraction, and cot

  • Always keep an eye on the 'target' expression – this can help suggest what identities to use

Examiner Tips and Tricks

  • Don't forget that you can start a proof from either side – sometimes it might be easier to start with a particular side

    • If you get stuck - try starting from the other side instead!

Worked Example

Prove that:

sec squared space x open parentheses cot squared space x minus cos squared space x close parentheses equals cot to the power of 2 space end exponent x

Use the definitions of sec space x equals fraction numerator 1 over denominator cos space x end fraction and cot space x space equals fraction numerator 1 over denominator tan space x end fraction equals fraction numerator cos space x over denominator sin space x end fraction, to rewrite the left hand side

fraction numerator 1 over denominator cos squared italic space x end fraction open parentheses fraction numerator cos squared space x over denominator sin squared space x end fraction space minus space cos squared space x close parentheses

Expand the brackets, using the fact that multiplying by fraction numerator 1 over denominator cos squared space x end fraction is the same as dividing by cos squared space x

fraction numerator 1 over denominator sin squared space x end fraction minus 1

Use the definition of cosec space x space equals fraction numerator space 1 over denominator sin space x end fraction to rewrite the expression

cosec squared space x space minus 1

Use the identity 1 plus cot squared space x space equals space cosec squared space x to rewrite the expression

1 plus cot squared space x space minus 1

Simplify to achieve the right hand side

bold cot to the power of bold 2 bold space bold italic x

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Solving Trigonometric EquationsNext:Permutations