IGCSEAdditional MathsCIERevision NotesCoordinate GeometryCoordinate Geometry of the CircleTangents to Circles

Tangents to Circles (CIE IGCSE Additional Maths)

Revision Note

Test yourself
Roger

Author

Roger

Last updated

Did this video help you?

Tangents to Circles

What is a tangent to a circle?

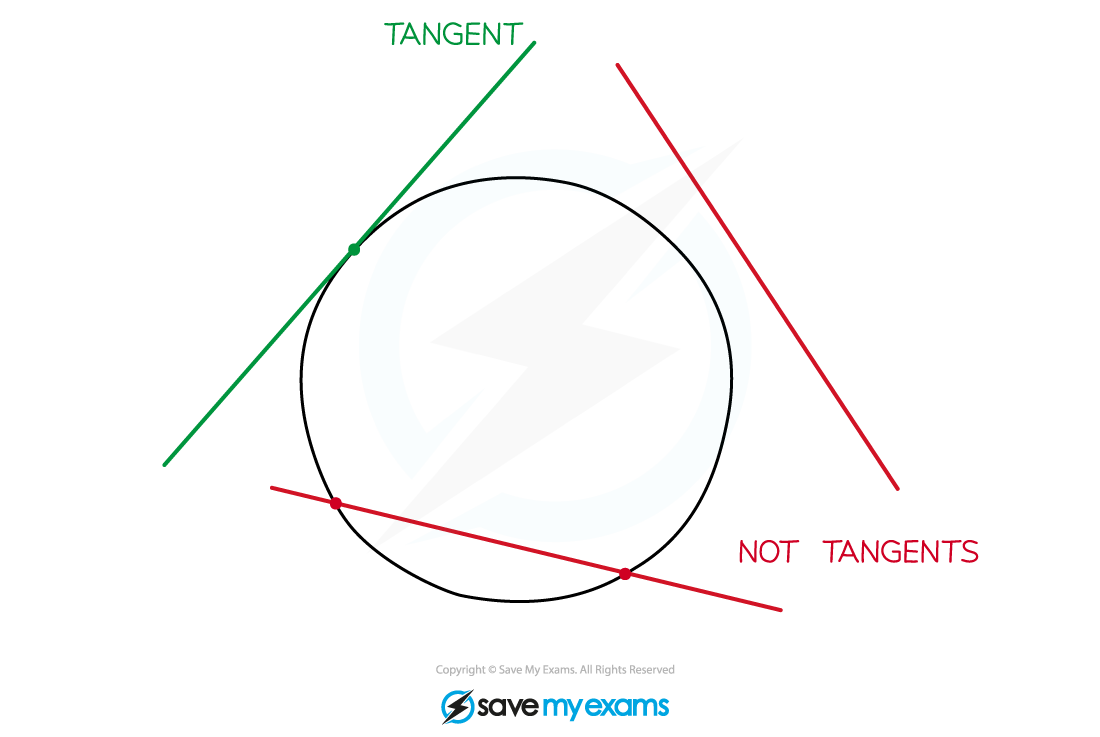
  • A tangent (to a circle) is a line that touches the circle at a single point but does not cut across the circleLines which are and are not tangents to a circle
  • A tangent to a circle is perpendicular to the radius of the circle at the point of intersection

The radius from the centre to a point is perpendicular to the tangent at that point

How can I find the equation of the tangent line to a circle at a given point?

Finding the equation of a tangent to a circle

  • STEP 1
    Find the gradient of the radius OP

Formula for the gradient of the radius

  • STEP 2
    Find the gradient of the tangent
    As they are perpendicular, if the gradient of the radius is m subscript r, then, the gradient of the tangent is m subscript t equals negative 1 over m subscript r
    (Negative reciprocal)
    Alternatively,

Formula for the gradient of a tangent

  • STEP 3
    The equation of the tangent is the equation of the line with that gradient that goes through point P (x2, y2)
    Write down the equation using y minus y subscript 2 equals m subscript t open parentheses x minus x subscript 2 close parentheseswhere m subscript tis the gradient

Examiner Tip

  • If you understand the formula in Step 2 above

Gradient of tangent equals negative fraction numerator x subscript 2 minus x subscript 1 over denominator y subscript 2 minus y subscript 1 end fraction

you can find the gradient of the tangent directly without having to find the gradient of the radius first.

Worked example

Radius & Tangent Example, A Level & AS Level Pure Maths Revision Notes

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Equation of a CircleNext:Intersection of Two Circles
    Roger

    Author: Roger

    Expertise: Maths

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.