Revision NotesExam QuestionsPast Papers
IGCSEAdditional MathsCIERevision NotesCoordinate GeometryCoordinate Geometry of the CircleEquation of a Circle

Equation of a Circle (CIE IGCSE Additional Maths)

Revision Note

Paul

Author

Paul

Last updated

Did this video help you?

Equation of a Circle

What is the equation of a circle?

  • A circle with centre (a, b) and radius r has the equation

 

Circle with centre (a,b) and radius r

  •  You need to be able to find the equation of a circle given its centre and radius
    • Substitute the values into the formula

 Finding the equation of a circle

How do I find the centre and radius of a centre given its equation?

  • Make sure it is in the form open parentheses x minus a close parentheses squared plus open parentheses y minus b close parentheses squared equals r squared
    • The radius is the positive square root of the constant term
    • The coordinates of the centre can be found by finding the values that make each bracket equal to zero

 

Finding the centre and radius of a circle given its equation

Examiner Tip

  • Remember that the numbers in the brackets have the opposite signs to the coordinates of the centreEqn of Circle sign flip, A Level & AS Level Pure Maths Revision Notes 
  • Don't forget to take the square root of the right-hand side of the equation when finding the radius

Worked example

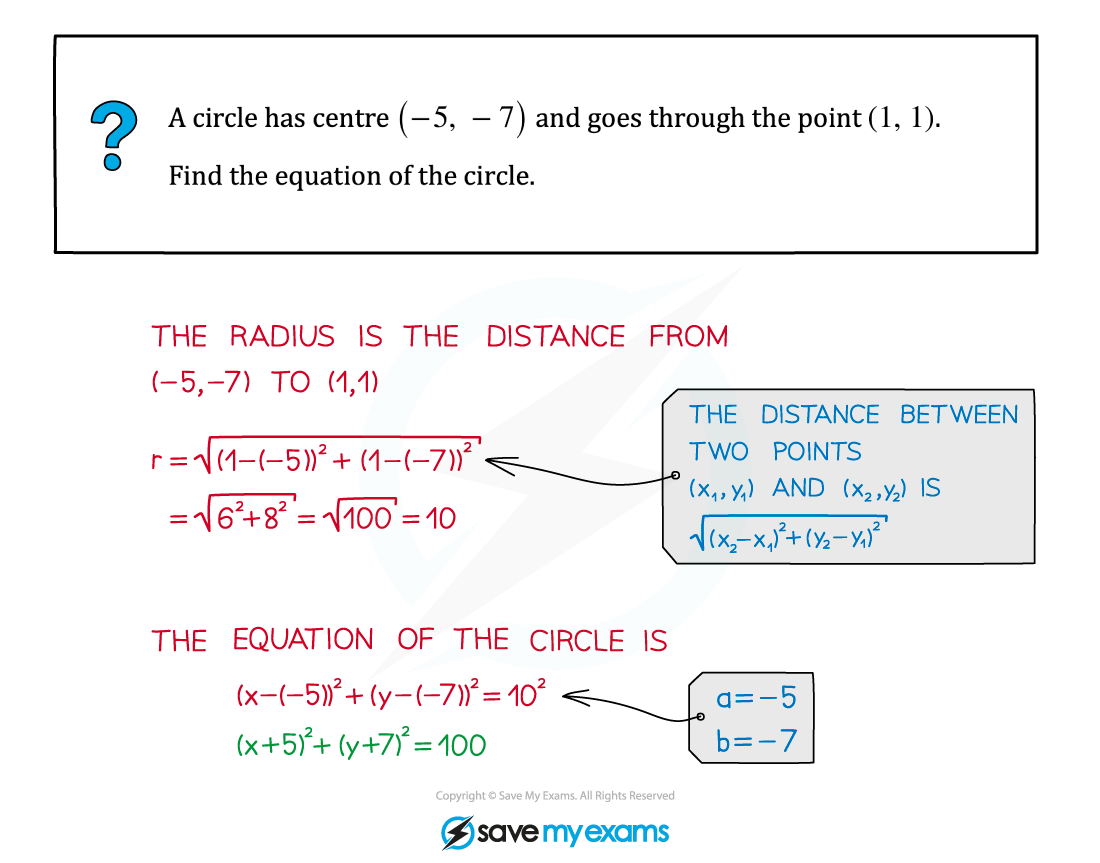
Eqn of Circle Example, A Level & AS Level Pure Maths Revision Notes

Did this video help you?

Finding the Centre & Radius

What are the different forms of the equation of a circle?

  • The most useful equation of a circle is open parentheses x minus a close parentheses squared plus open parentheses y minus b close parentheses squared equals r squared
    • This is so the centre, open parentheses a comma space b close parentheses and radius r are easy to see
  • Any other form of the equation of a circle can be rearranged into this form
    • The most common alternative form for the equation of a circle is called the general form
      x squared plus y squared plus 2 g x plus 2 f y plus c equals 0

How do I find the centre and radius of a circle from any form of its equation?

  • A circle equation in a different form can always be rearranged into (x- a)2 + (y - b)2 = r2
    • The centre is then open parentheses a comma space b close parentheses and radius r
  • Rearranging to this form will often involve completing the square

Completing the square to find the centre and radius of a circle

Worked example

Circle Ctr Rad Example, A Level & AS Level Pure Maths Revision Notes

Intersection of a Circle & a Line

What is meant by the intersection of a circle and a line?

  • A line may pass through a circle
    • in which case it will intersect the circle twice
    • the part of the line between the two points of intersection will be a chord
      • or, if it passes through the centre of the circle, a diameter
  • A line may touch a circle
    • in which case it will intersect the circle once
    • such a line would be called a tangent to the circle
  • A line may not intersect a circle at all

The three cases for intersections between a circle and a lin

How do I determine whether a line and a circle intersect?

  • For the equation of a circle in the form open parentheses x minus a close parentheses squared plus open parentheses y minus b close parentheses squared equals r squared and the equation of a line in the form y equals m x plus c
  • STEP 1
    Substitute the linear equation into the circle equation
    • e.g.
      open parentheses x minus 5 close parentheses squared plus open parentheses y minus 2 close parentheses squared equals 13 and y equals x minus 4
      would become
      open parentheses x minus 5 close parentheses squared plus open parentheses open parentheses x minus 4 close parentheses minus 2 close parentheses squared equals 13

  • STEP 2
    Expand, rearrange and simplify this equation - it should be a quadratic
    • e.g.
      open parentheses x minus 5 close parentheses squared plus open parentheses x minus 6 close parentheses squared equals 13
      x squared minus 10 x plus 25 plus x squared minus 12 x plus 36 minus 13 equals 0
      x squared minus 11 x plus 24 equals 0
  • STEP 3
    Solve the equation to deduce the number of intersections
    If there are two solutions, there are two intersections, one solution (repeated) indicates a tangent, no (real) solutions indicates no intersection
    • e.g.  
      open parentheses x minus 3 close parentheses open parentheses x minus 8 close parentheses equals 0 x equals 3 comma space space x equals 8
      Two solutions so the line and the circle intersect twice
  • STEP 4
    If required, find the y-coordinates of the intersection(s)
    • e.g.
      y equals x minus 4 y equals 3 minus 4 equals negative 1 comma space space y equals 8 minus 4 equals 4
      The line and the circle intersect at the points open parentheses 3 comma space minus 1 close parentheses and open parentheses 8 comma space 4 close parentheses

Examiner Tip

  • A horizontal or vertical line could intersect a circle, when the full method shown above is unnecessary
    • Horizontal lines have the form y equals k, so substitute k for y in the circle equation (and solve for x)
    • Vertical lines have the form x equals k, so substitute k for x in the circle equation (and solve for y)

Worked example

Show that the line y equals 4 x plus 4 is tangent to the circle open parentheses x minus 4 close parentheses squared plus open parentheses y minus 3 close parentheses squared equals 17.
State the coordinates of the point of intersection between the tangent and the circle.

STEP 1 - Substitute the linear equation into the circle equation

open parentheses x minus 4 close parentheses squared plus open parentheses 4 x plus 4 minus 3 close parentheses squared equals 17

STEP 2 - Rearrange to a quadratic

table row cell open parentheses x minus 4 close parentheses squared plus open parentheses 4 x plus 1 close parentheses squared minus 17 end cell equals 0 row cell x squared minus 8 x plus 16 plus 16 x squared plus 8 x plus 1 minus 17 end cell equals 0 row cell 17 x squared end cell equals 0 end table

STEP 3 - Solve

x squared equals 0

x equals 0 (repeated)

There is only one point of intersection so the line bold italic y bold equals bold 4 bold italic x bold plus bold 4 is tangent to the circle

STEP 4 - The coordinates are required

y equals 4 open parentheses 0 close parentheses plus 4 equals 4

The line and circle intersect at stretchy left parenthesis 0 comma space 4 stretchy right parenthesis

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Parallel & Perpendicular LinesNext:Tangents to Circles
    Paul

    Author: Paul

    Expertise: Maths

    Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams – one of the many reasons he is excited to be a member of the SME team.