Laws of Logarithms (CIE IGCSE Additional Maths)

Revision Note

Test yourself

Author

Amber

Last updated

12 September 2023

Did this video help you?

Laws of Logarithms

What are the laws of logarithms?

Laws of logarithms allow you to simplify and manipulate expressions involving logarithms
- The laws of logarithms are equivalent to the laws of indices
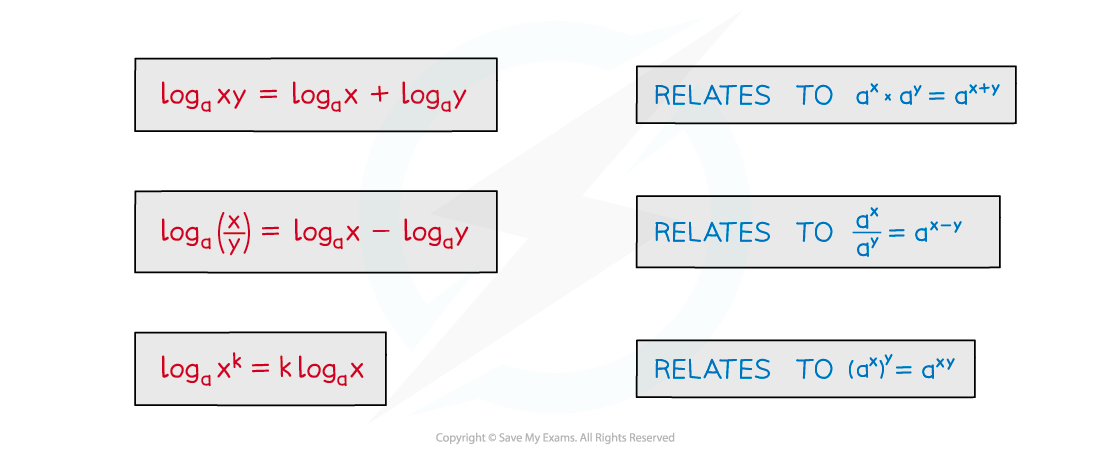
The laws you need to know are, given $a, x, y > 0$ :
- $\log_{a} x y = \log_{a} x + \log_{a} y$
  - This relates to $a^{x} \times a^{y} = a^{x + y}$
- $\log_{a} \frac{x}{y} = \log_{a} x {- \log}_{a} y$
  - This relates to $a^{x} \div a^{y} = a^{x - y}$
- $\log_{a} x^{m} = m \log_{a} x$
  - This relates to $(a^{x})^{y} = a^{x y}$

The laws of logarithms

There are also some particular results these lead to
- $\log_{a} a = 1$
- $\log_{a} a^{x} = x$
- $a^{\log_{a} x} = x$
- $\log_{a} 1 = 0$
- $\log_{a} (\frac{1}{x}) = - \log_{a} x$

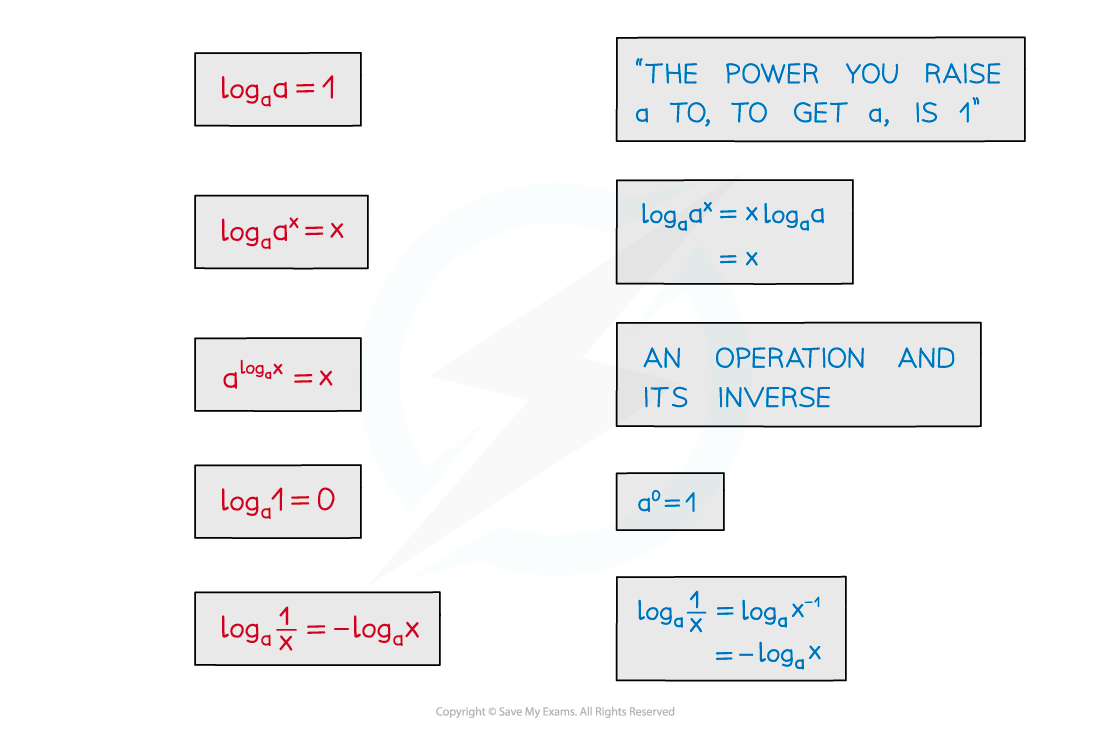
Properties of logarithms

Beware…
- … $\log_{a} (x + y) \neq \log_{a} x + \log_{a} y$
These results apply to $\ln x (\log_{e} x)$ too
- Two particularly useful results are
  - $\ln e^{x} = x$
  - $e^{\ln x} = x$

How do I use the laws of logarithms?

Laws of logarithms can be used to …
- … simplify expressions
- … solve logarithmic equations
- … solve exponential equations

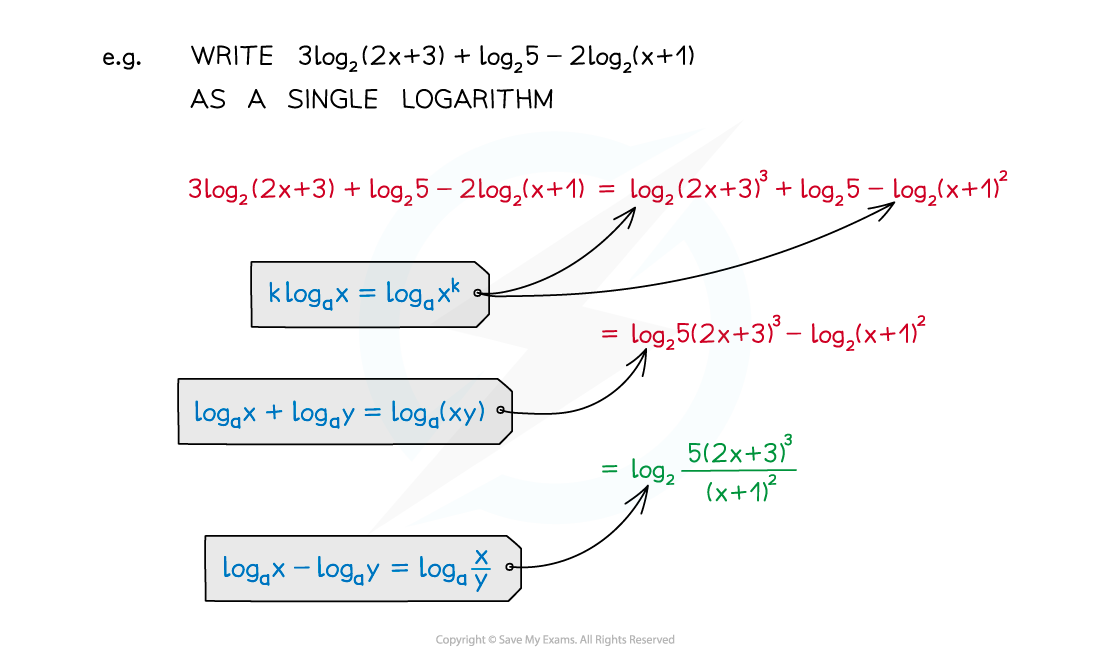
Simplifying an expression using the laws of logarithms

Examiner Tip

Remember to check whether your solutions are valid
- log (x+k) is only defined if x > -k
- You will lose marks if you forget to reject invalid solutions

Worked example

Write the expression

2 \log 4 - \log 2

in the form

\log k

, where

k \in ℤ

Using the law

\log_{a} x^{m} = m \log_{a} x

we can rewrite

2 \log 4

\log 4^{2} = \log 16

2 \log 4 - \log 2 = \log 16 - \log 2

Using the law

\log_{a} \frac{x}{y} = \log_{a} x - \log_{a} y

\log 16 - \log 2 = \log \frac{16}{2} = \log 8

2 \log 4 - \log 2 = \log 8

b) Hence, or otherwise, solve

2 \log 4 - \log 2 = - \log \frac{1}{x}

Rewrite the equation using the expression found in part (a).

2 \log 4 - \log 2 = \log 8

\log 8 = - \log \frac{1}{x}

Using the index law

\frac{1}{x} = x^{- 1}

\log 8 = - \log x^{- 1}

Using the law

\log_{a} x^{m} = m \log_{a} x

\log 8 = \log x^{- (- 1)} = \log x

Compare the two sides.

\log 8 = \log x

x = 8

Change of Base

How do I change the base of a logarithm?

The formula for changing the base of a logarithm is

$\log_{a} x = \frac{\log_{b} x}{\log_{b} a}$

The value you choose for b does not matter, however if you do not have a calculator, you can choose b such that the problem will be possible to solve

Why change the base of a logarithm?

The laws of logarithms can only be used if the logs have the same base
- If a problem involves logarithms with different bases, you can change the base of the logarithm and then apply the laws of logarithms
Changing the base of a logarithm can be particularly useful if you need to evaluate a log problem without a calculator
- Choose the base such that you would know how to solve the problem from the equivalent exponent

This formula had more use when calculators were less advanced
- Some old calculators only had a button for logarithm of base 10
- To calculate $\log_{5} 7$ on these calculators you would have to enter
  - $\frac{\log_{10} 7}{\log_{10} 5}$

The formula can be useful when evaluating a logarithm where the two numbers are powers of a common number
- $\log_{4} 8 = \frac{\log_{2} 8}{\log_{2} 4} = \frac{3}{2}$
The formula can be useful when you are solving equations and two logarithms have different bases
- For example, if you have $\log_{3} k$ and $\log_{9} n$ within the same equation
  - You can rewrite $\log_{9} n$ as $\frac{\log_{3} n}{\log_{3} 9}$ which simplifies to $\frac{1}{2} \log_{3} n$
  - Or you can rewrite $\log_{3} k$ as $\frac{\log_{9} k}{\log_{9} 3}$ which simplifies to $2 \log_{9} k$
The formula also allows you to derive and use a formula for switching the numbers:

$\log_{a} x = \frac{1}{\log_{x} a}$

- Using the fact that $\log_{x} x = 1$

Examiner Tip

It is very rare that you will need to use the change of base formula
Only use it when the bases of the logarithms are different

Worked example

By choosing a suitable value for b, use the change of base law to find the value of $\log_{8} 32$ without using a calculator.

Note that 8 and 32 are both powers of 2, where 8 = 2³ and 32 = 2⁵.

Therefore we can choose b = 2 in the change of base formula.

$\log_{a} x = \frac{\log_{b} x}{\log_{b} a}$ :

$\log_{8} 32 = \frac{\log_{2} 32}{\log_{2} 8}$

If 2³ = 8 then log₂8 = 3 and if 2⁵ = 32 then log₂32 = 5.

$\frac{\log_{2} 32}{\log_{2} 8} = \frac{5}{3}$

$\log_{8} 32 = \frac{5}{3} = 1 \frac{2}{3}$

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself

Did this page help you?

Previous:Logarithmic FunctionsNext:Exponential Equations

Laws of Logarithms (CIE IGCSE Additional Maths)

Revision Note

What are the laws of logarithms?

How do I use the laws of logarithms?

How do I change the base of a logarithm?

Why change the base of a logarithm?

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Amber