Polynomial Division (CIE IGCSE Additional Maths)

Revision Note

Test yourself

Author

Roger

Last updated

12 September 2023

Did this video help you?

Polynomial Division

What is polynomial division?

Polynomial division is the process of dividing two polynomials
- This is usually only useful when the degree of the denominator is less than or equal to the degree of the numerator

Polynomial division is a method for splitting polynomials into factor pairs
- (with or without a remainder term)

expressing a polynomial as a pair of factors

The main uses of polynomial division are
- factorising polynomials
- simplifying 'top-heavy' algebraic fractions

How do I divide polynomials?

The method used for polynomial division is just like the long division method for numbers
- sometimes called the 'bus stop method'

The answer to a polynomial division question is built up term by term
- Start by dividing by the highest power term
- Write out this multiplied by the divisor and subtract

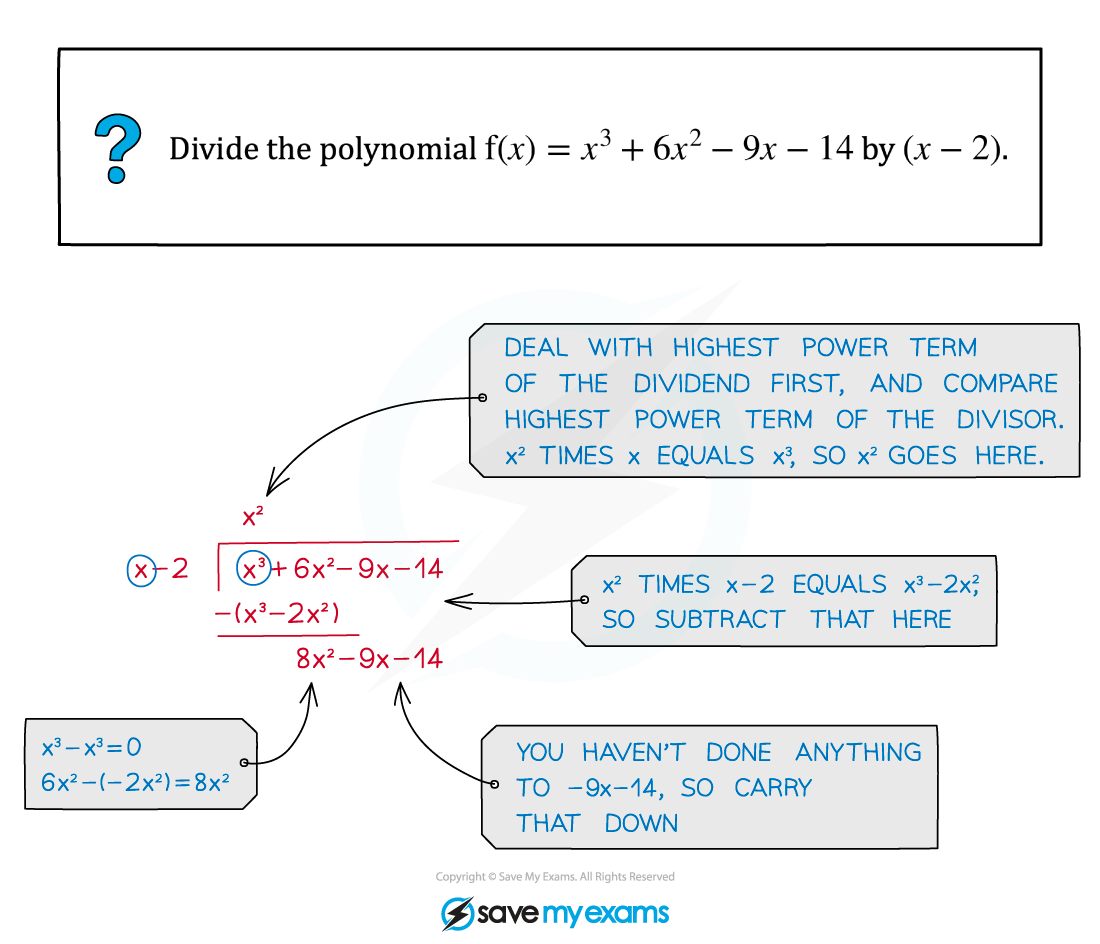
polynomial division example with bus stop method pt1

Continue to divide by each reducing power term and subtracting your answer each time

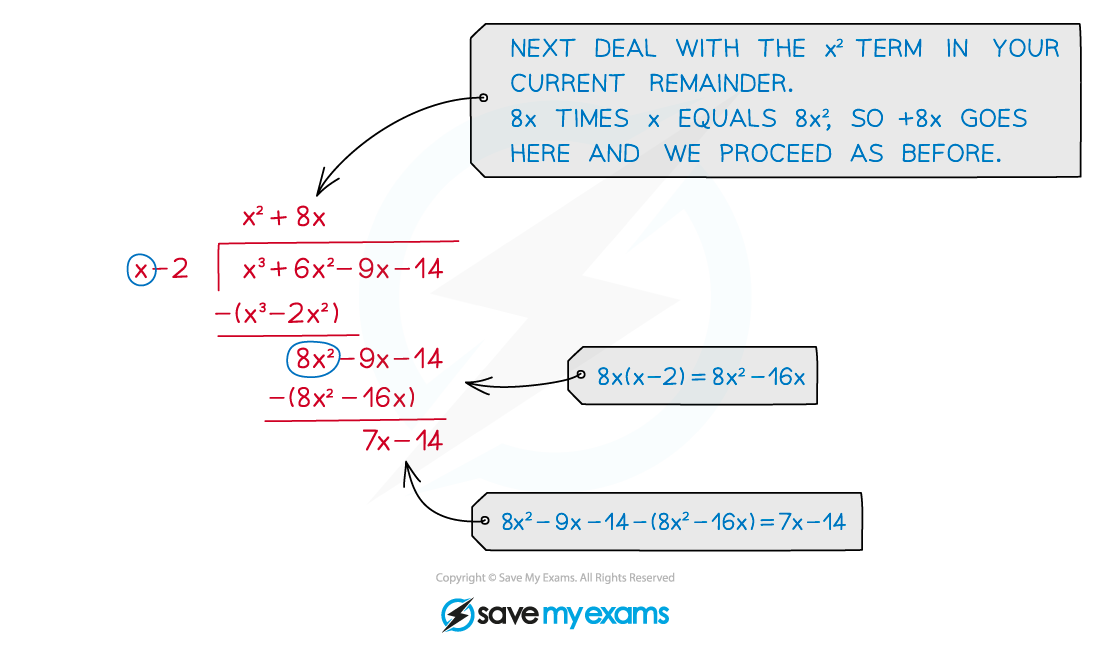
polynomial division example with bus stop method pt2

Continue until you are left with zero

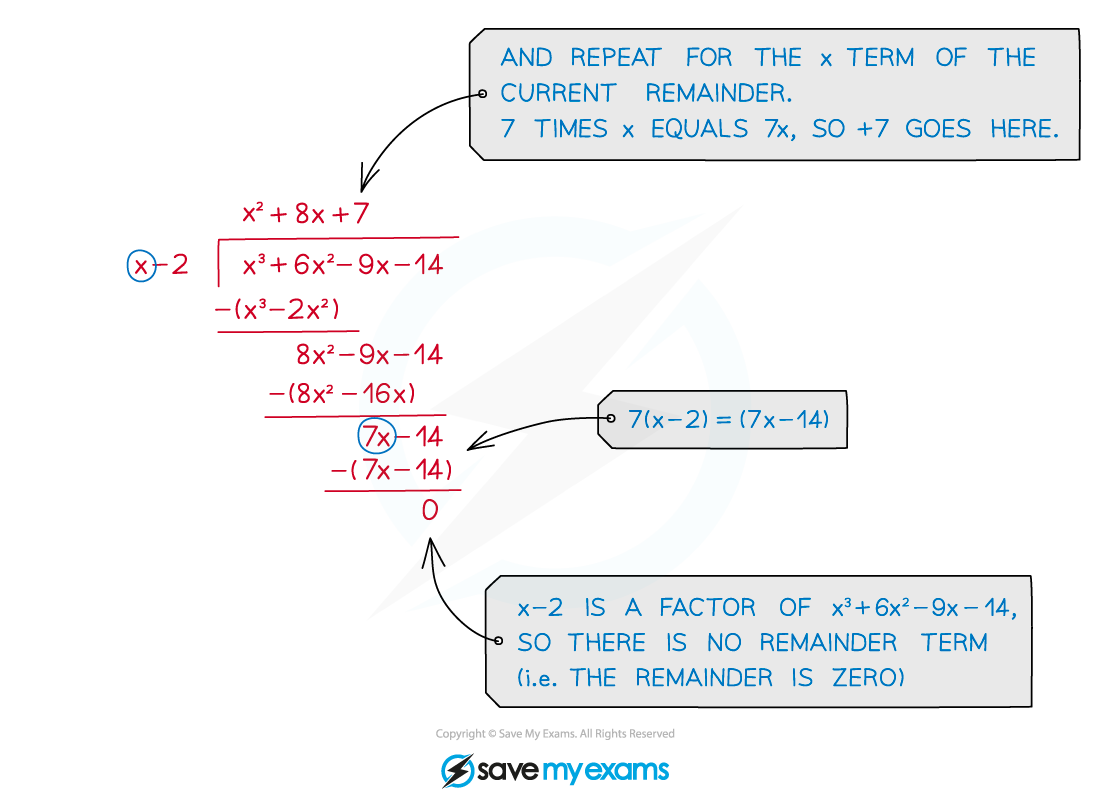
polynomial division example with bus stop method pt3

If the divisor is not a factor of the polynomial then there will be a remainder term left at the end of the division

Worked example

For the polynomial $f (x) = x^{4} + 11 x^{2} - 1$ divide $f (x)$ by $x + 3$ and write the remainder.

Set up the polynomial division ('bus stop')

There is no $x^{3}$ term so write this as $0 x^{3}$ in the method.
There is no $x$ term so write this as $0 x$ in the method.

The first division step to consider is $x^{4} \div x$ .

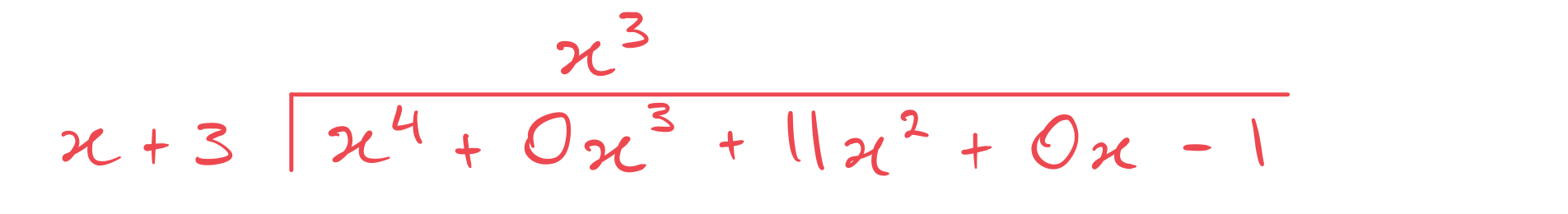
cie-add-maths-polynomial-division-we-solution-a-part-i

.Multiply $x^{3}$ by $x + 3$ and subtract from $x^{4} + 0 x$ .

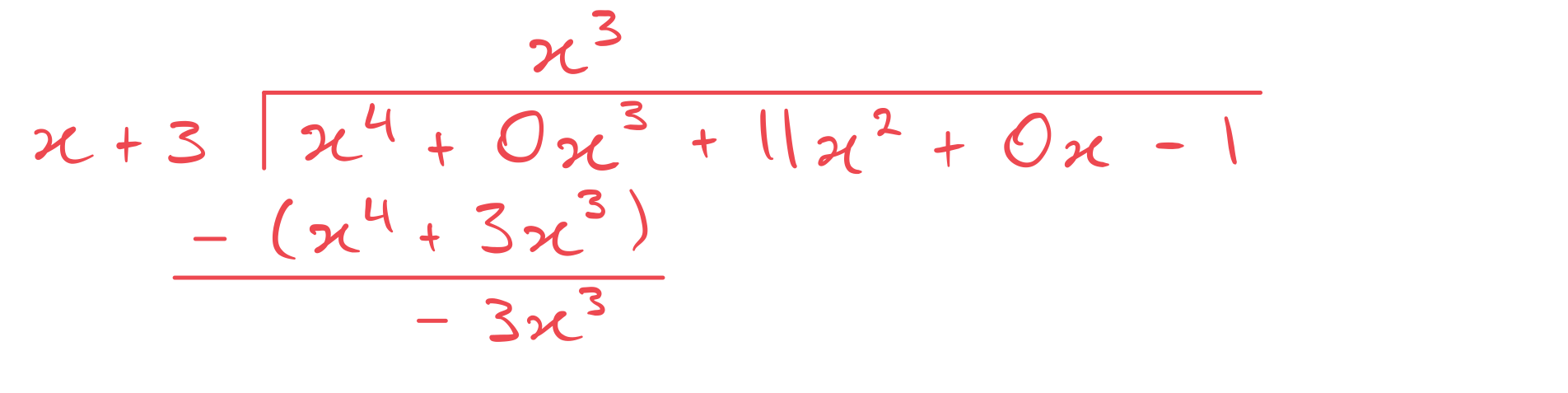
cie-add-maths-polynomial-division-we-solution-a-part-ii

Bring the $11 x^{2}$ down and divide $- 3 x^{3}$ by $x$ . Continue with each step until you are finished.

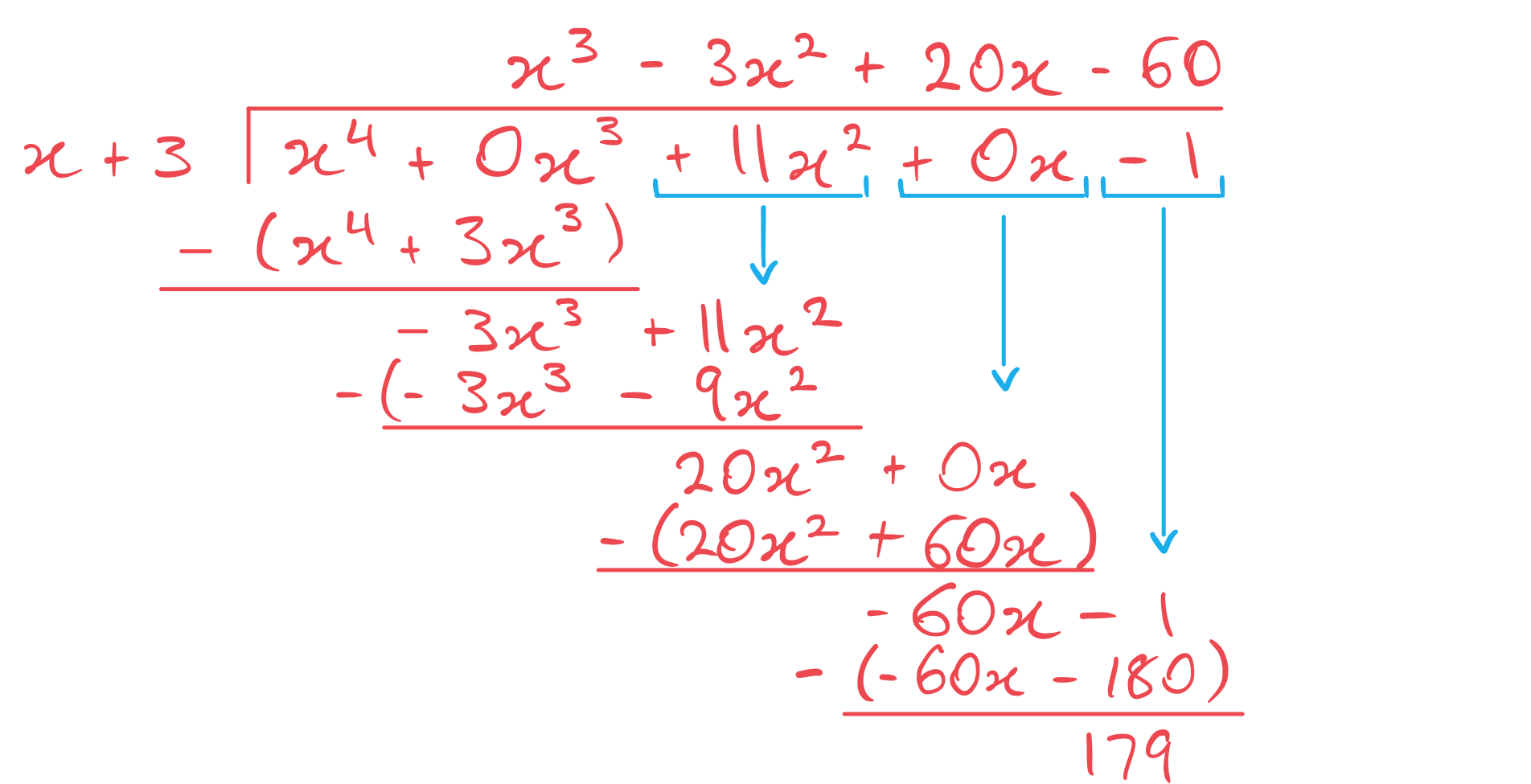
cie-add-maths-polynomial-division-we-solution-a-part-iii

The remainder is 179.

Quadratic Divisor

What is meant by a quadratic divisor?

Polynomial division usually involves dividing by a linear term
- a term of the form $(x + p)$ where $p$ is a constant and usually an integer
It is possible to divide a polynomial by a quadratic term (and cubic, etc)
- this would be a term of the form $(x^{2} + q x + r)$ where $q$ and $r$ are constants
- this is what is meant by a quadratic divisor

How do I divide by a quadratic divisor?

The process is the same as for a linear divisor
- However, as $x^{2}$ will not divide into $x$ (in the polynomial division sense at least) the remainder, if there is one, could be of linear form, i.e. $(r x + s)$ where $r$ and $s$ are constants
  - It is possible that $r = 0$ and so the remainder is still a constant

Examiner Tip

Give yourself plenty of room to do polynomial division
- Not only will this help avoid errors, it will make your working clear
If you make a mistake and change something, fine, but if your method starts to get too messy it is best to restart

Worked example

Find the remainder when $x^{4} + 4 x^{3} - x + 1$ is divided by $x^{2} - 2 x$ .

Set up the polynomial division ('bus stop') - there is no $x^{2}$ term so write this as $0 x^{2}$ in the method.

The first division step to consider is $x^{4} \div x^{2}$ .

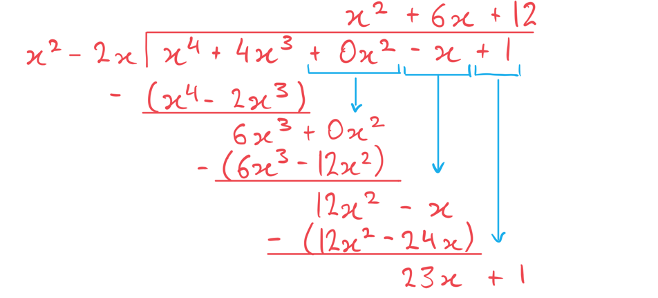
bus stop method for polynomial division with a quadratic divisor

The remainder is $23 x + 1$ .

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: