Methods of Depreciation (Edexcel IGCSE Accounting): Revision Note
Exam code: 4AC1
Straight line depreciation
What is the straight line method of depreciation?
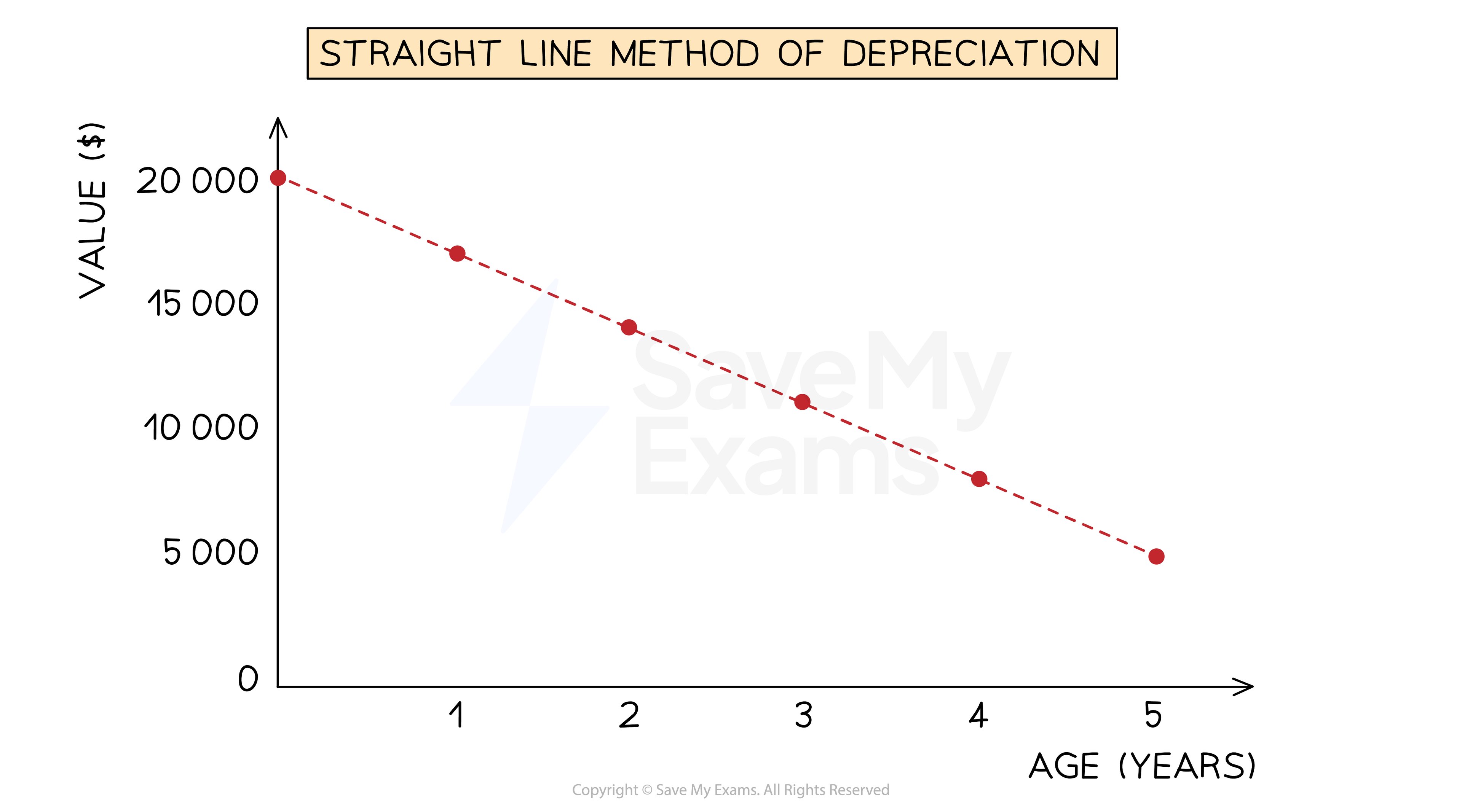
The straight line method of depreciation assumes that a non-current asset loses value at a constant rate over its useful life
This means that the expense for its depreciation is the same each year
The carrying value can reach $0
This is when the asset is fully depreciated
You could be given the depreciation rate as a percentage of its original value
E.g. depreciation could be charged at 20% of its original cost
Or you could be expected to calculate the depreciation using:
The number of years that the non-current asset will be used
The expected value of the non-current asset at the end of its working life
This value could be $0
The expected value is also called the residual value or the disposal value
This method is usually used when the asset will be equally valuable for each year of its use
For example, fixtures and fittings, equipment, etc
How do I calculate depreciation using the straight line method?
If you are given the percentage for the depreciation
Find the percentage of the original amount
This will be the yearly depreciation charge
If you are not given the percentage
Calculate the expected loss in value during the expected life of the non-current asset
The original value minus the expected value at the end of its life
Divide the loss by the number of years it will be used
This will be the yearly depreciation charge
Examiner Tips and Tricks
The straight line method is similar to simple interest calculations used in maths.
Worked Example
Abi purchases machinery for $18 000. Machinery is depreciated at 15% per annum using the straight line method.
Calculate the carrying value of the machinery after 3 years.
Answer
Calculate the yearly expense due to depreciation
15% ✕ $18 000 = $2 700
Calculate the total depreciation after 3 years
3 ✕ $2 700 = $8 100
Subtract the depreciation from the original value
$18 000 - $8 100 = $9 900
Worked Example
Taiki purchases a vehicle for $30 000. He expects to use the vehicle for 3 years, after which he estimates that it will have a value of $12 000.
Calculate the yearly expense due to the depreciation of the vehicle.
Answer
Calculate the loss in value over the 3 years
$30 000 - $12 000 = $18 000
Divide this by the number of years
$18 000 ÷ 3 = $6 000
Reducing balance depreciation
What is the reducing balance method of depreciation?
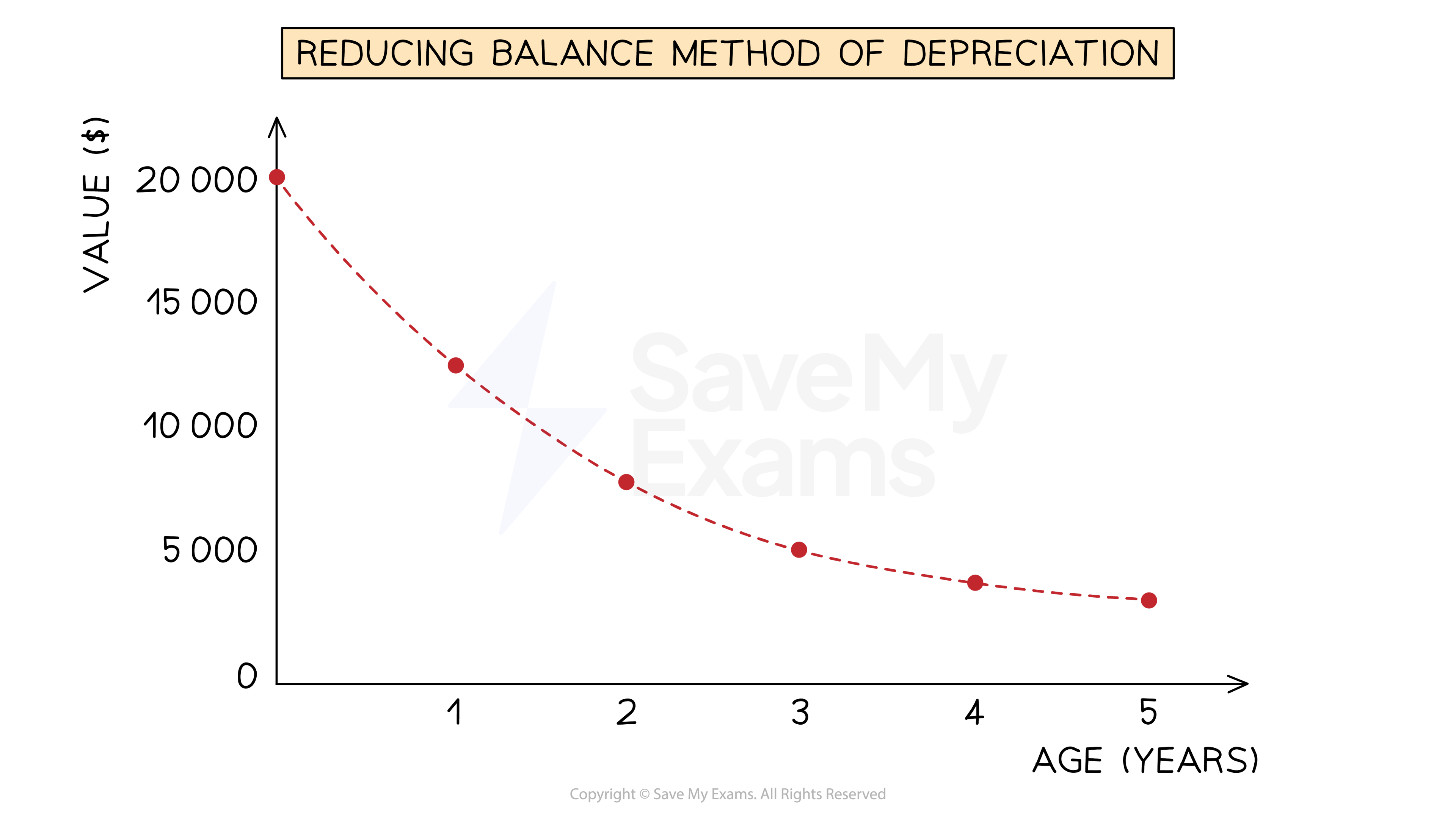
The reducing balance method of depreciation assumes that the non-current asset loses value at a rate proportional to its current value
This means that the expense for its depreciation gets smaller each year as the current value decreases
You will be told the percentage of the current value to use for depreciation
This method is usually used when a non-current asset initially loses value at a fast rate
How do I calculate depreciation using the reducing balance method?
Find the percentage of the current carrying value
This will be the depreciation charge for that year
If you need to calculate the depreciation for multiple years, then calculate one year at a time
Find the depreciation charge for one year using the carrying value at that start of the year
Subtract this amount from the carrying value at the start of the year to find the new carrying value
Find the depreciation charge for the next year using the carrying value at the start of that year
Continue this process
If you just need to find the current carrying value then you can use some maths skills
Subtract the percentage from 100%
Write this as a decimal
Raise this to the power of the number of years
Multiply this by the original value
Examiner Tips and Tricks
The reducing balance method is similar to compound interest calculations used in maths.
Amounts should always be given to the nearest dollar in exams.
Worked Example
Abi purchases a vehicle for $16 000. Machinery is depreciated at 25% per annum using the reducing balance method.
Calculate the carrying value of the machinery after 3 years.
Answer
Find the depreciation charged in each year by finding the percentage of the carrying value at that time.
Subtract that year’s depreciation from the carrying value to find the carrying value at the end of the year.
End of year | Depreciation charge | Carrying value |
0 | - | $16 000 |
1 | 25% ✕ $16 000 = $4 000 | $16 000 - $4 000 = $12 000 |
2 | 25% ✕ $12 000 = $3 000 | $12 000 - $3 000 = $9 000 |
3 | 25% ✕ $9 000 = $2 250 | $9 000 - $2 250 = $6 750 |
Alternatively:
Subtract the percentage from 100%
100% - 25% = 75%
Write this as a decimal
75% = 0.75
Raise this to the power of the number of years
0.753
Multiply this by the original value
$16 000 ✕ 0.753 = $6 750

Unlock more, it's free!
Did this page help you?