Methods of Depreciation (Edexcel IGCSE Accounting): Revision Note

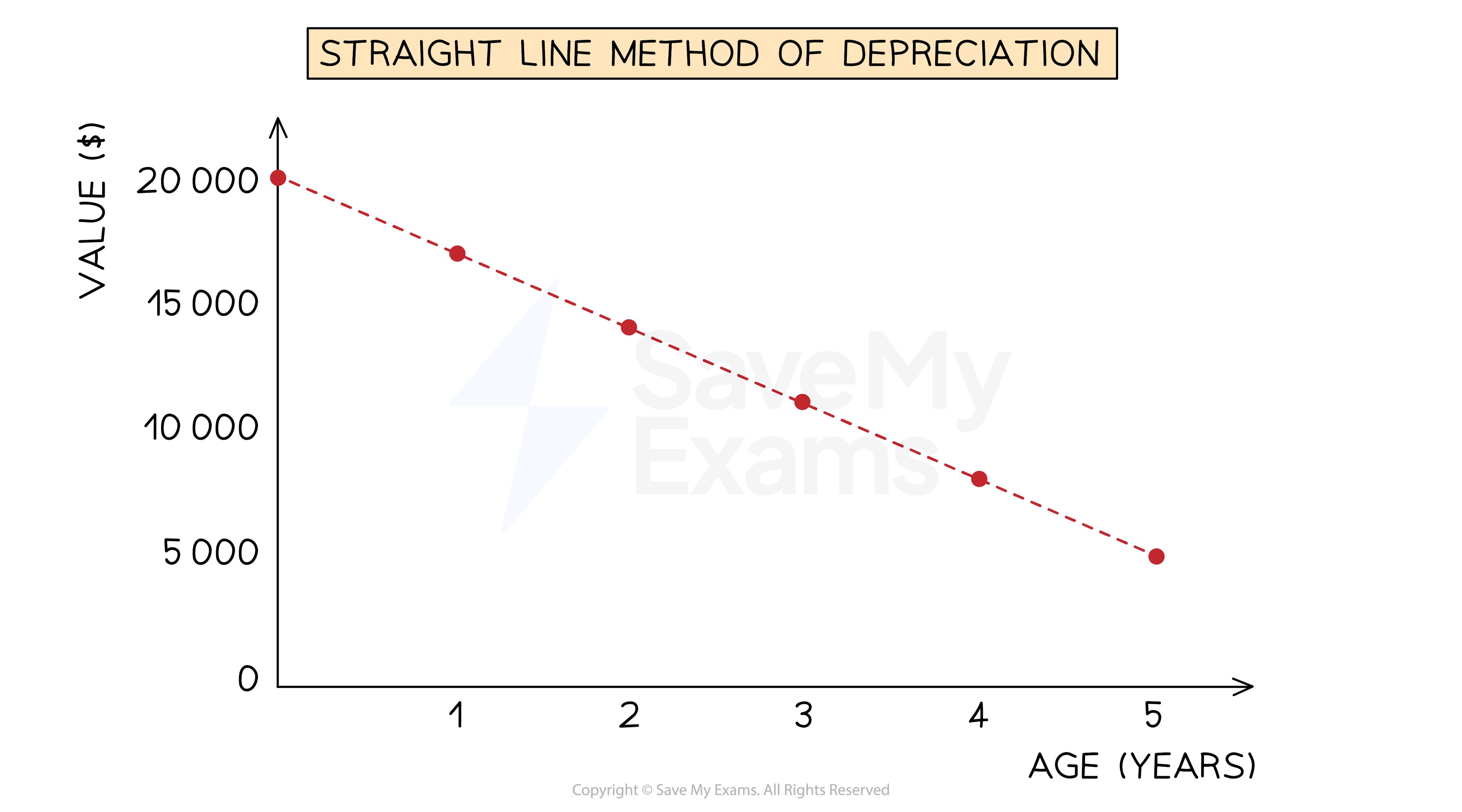
The straight line method of depreciation assumes that a non-current asset loses value at a constant rate over its useful life

• This means that the expense for its depreciation is the same each year

• The carrying value can reach $0

  • This is when the asset is fully depreciated

You could be given the depreciation rate as a percentage of its original value

• E.g. depreciation could be charged at 20% of its original cost

Or you could be expected to calculate the depreciation using:

• The number of years that the non-current asset will be used

• The expected value of the non-current asset at the end of its working life

  • This value could be $0

  • The expected value is also called the residual value or the disposal value

This method is usually used when the asset will be equally valuable for each year of its use

• For example, fixtures and fittings, equipment, etc

If you are given the percentage for the depreciation

• Find the percentage of the original amount

• This will be the yearly depreciation charge

If you are not given the percentage

• Calculate the expected loss in value during the expected life of the non-current asset

  • The original value minus the expected value at the end of its life

• Divide the loss by the number of years it will be used

• This will be the yearly depreciation charge

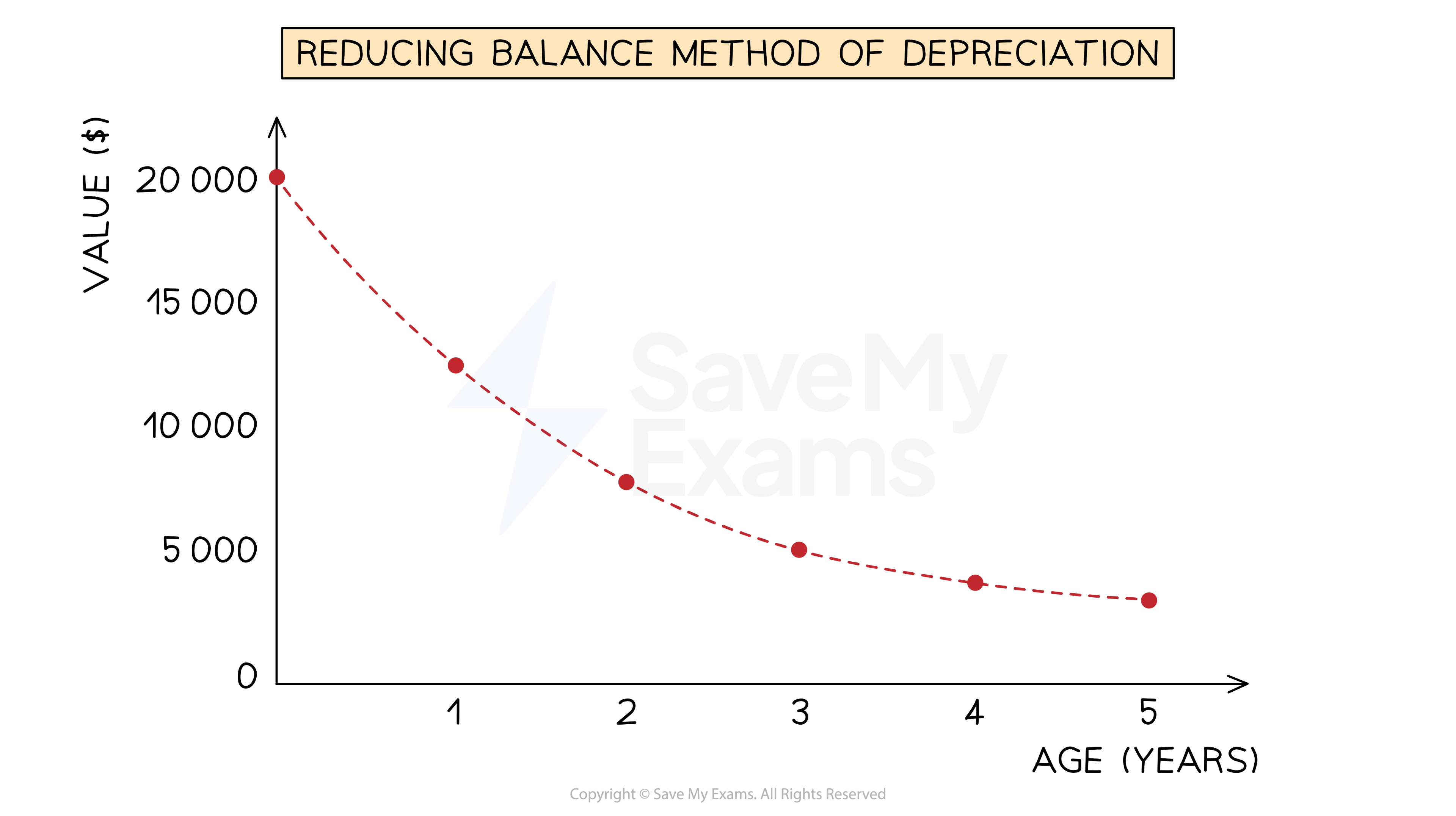
The reducing balance method of depreciation assumes that the non-current asset loses value at a rate proportional to its current value

• This means that the expense for its depreciation gets smaller each year as the current value decreases

You will be told the percentage of the current value to use for depreciation

This method is usually used when a non-current asset initially loses value at a fast rate

Find the percentage of the current carrying value

• This will be the depreciation charge for that year

If you need to calculate the depreciation for multiple years, then calculate one year at a time

• Find the depreciation charge for one year using the carrying value at that start of the year

• Subtract this amount from the carrying value at the start of the year to find the new carrying value

• Find the depreciation charge for the next year using the carrying value at the start of that year

• Continue this process

If you just need to find the current carrying value then you can use some maths skills

• Subtract the percentage from 100%

• Write this as a decimal

• Raise this to the power of the number of years

• Multiply this by the original value