GlossariesAP® GlossariesAP® Calculus AB GlossarySqueeze Theorem: AP® Calculus Definition

Squeeze Theorem: AP® Calculus Definition - AP® Calculus AB Definition

Reviewed by: Roger B

Published

What is the squeeze theorem in AP® Calculus?

The squeeze theorem (also known as the sandwich theorem) is a fundamental principle in calculus that assists in determining the limit of a function. It is particularly useful when the limit of a function is difficult to evaluate directly.

The theorem states that:

  • If you have two functions, g open parentheses x close parentheses and h open parentheses x close parentheses, which bound a third function f open parentheses x close parentheses such that g open parentheses x close parentheses less or equal than f open parentheses x close parentheses less or equal than h open parentheses x close parentheses for all xin some interval around a point (excluding the point itself if necessary)

  • and if the limits of g open parentheses x close parentheses and h open parentheses x close parentheses as x approaches a particular value are equal

  • then the limit of f open parentheses x close parentheses as x approaches that value must also be the same

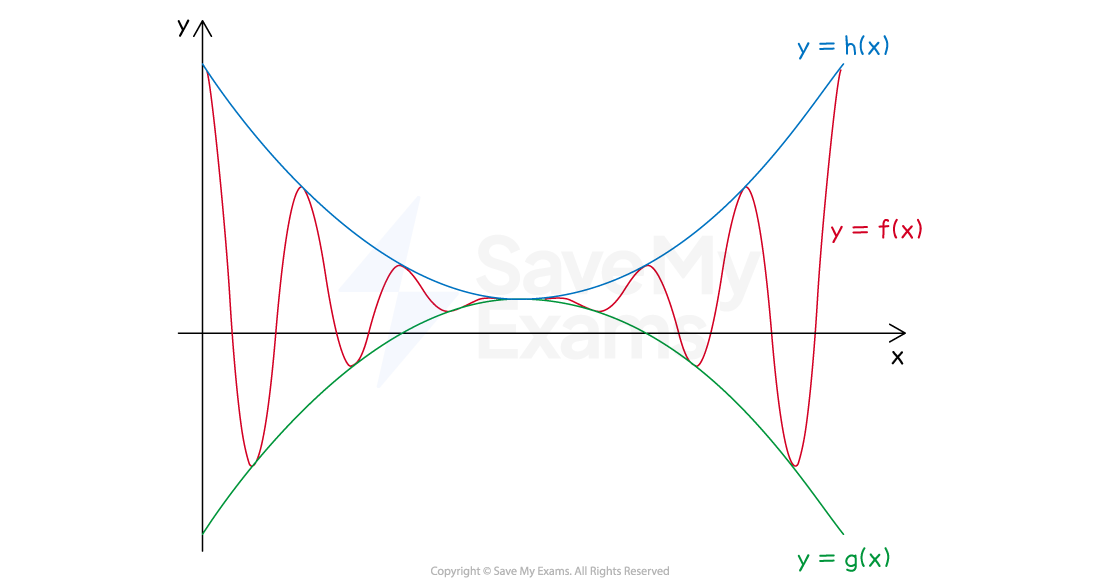
A graph illustrating the squeeze theorem, with the graph of f(x) 'squeezed' between the graphs of g(x) and h(x)

This theorem is particularly pertinent in AP® Calculus as it provides a robust technique for solving limits where direct substitution might be challenging or where functions exhibit indeterminate forms.

Squeeze theorem study resources to ace your exams

Save My Exams has a great range of resources to help you explore the squeeze theorem in more detail. Try this study guide on the topic, then have a go at some multiple choice and free response exam questions.

Explore our Calculus AB and Calculus BC study resources.

Examiner-written AP® Calculus AB revision resources that improve your grades 2x

  • Written by expert teachers and examiners
  • Aligned to exam specifications
  • Everything you need to know, and nothing you don’t
AP® Calculus AB revision resources

Share this article

Roger B

Reviewer: Roger B

Expertise: Maths Content Creator

Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.

The examiner written revision resources that improve your grades 2x.

Join now